Перестановки без фіксованих пар

 

Позначимо через 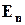 число таких перестановок чисел 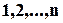, що жодна з цих перестановок не містить жодної з упорядкованих фіксованих пар:

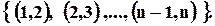
Розв’язання.

Для обчислення 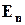 використовуємо принцип включення і виключення. Позначимо через  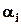властивість перестановки містити 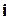-ту впорядковану пару 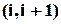. Для обчислення скористаємося другим окремим випадком для формули включень-виключень. Число всіх перестановок 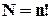. Перестановки, що володіють властивістю 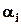, виходять як перестановки елементів  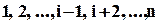та пари 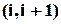, що розглядається. як один елемент. Отже, незалежно від  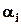маємо: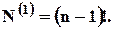

Для перестановок, що володіють двома властивостями, тобто мають дві впорядковані пари, наприклад 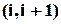 та , розглянемо два випадки:

1) 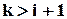, пари йдуть не поспіль;

2) 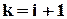, пари розташовані одна за одною.

1) Якщо 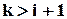, то пари йдуть не поспіль.

У цьому випадку маємо перестановки двох пар, як окремих, складних елементів: 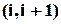та  і 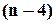 елемента, що лишилися. Тобто всього переставляються  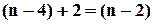елемента.

2) Якщо 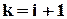, то перестановки складаємо з однієї впорядкованої трійки елементів:  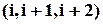та 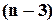 інших елементів, тобто теж із  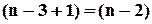елементів.

Таким чином, число перестановок, що володіють двома властивостями, так само: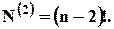

Аналогічно, число перестановок, що володіють 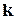 властивостями, залежить тільки від  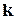і дорівнює: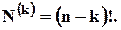

Тоді, загальне число перестановок без фіксованих пар дорівнює:

 

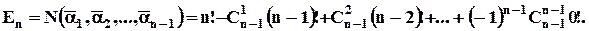
Наприклад.

1. Скільки різних слів можна згенерувати із букв слова "тік-так", щоб ніякі однакові букви не йшли одна за одною?

Розв’язання.

Вcього в слові "тік-так": 6 букв серед яких дві букви "к" і дві букви "т".

Нехай 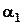 – дві букви "т" йдуть одна за одною;

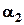 – дві букви "к" ідуть одна за одною.

Тоді , маємо:

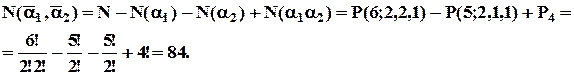
2. Скількома способами можна переставити цифри у числі 123 123 так, щоб ніякі дві однакові цифри не знаходилися поруч?

Розв’язання.

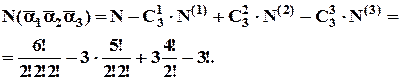
3. Пустелею йде караван із 5 верблюдів. Подорож триває багато днів і нарешті, усім набридає бачити попереду себе одного й того ж верблюда. Скількома способами можна переставити верблюдів так, щоб попереду кожного верблюда йшов інший, ніж раніше?

Розв’язання.

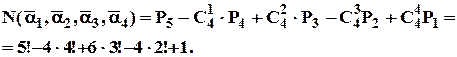
Завдання до лабораторної роботи

Відповідно до заданого варіанту розв’язати задачі перерахунку.

 

Варіант №1.

1. Чоловік має 6 друзів, і протягом  20 днів запрошує до себе 3 з них так, що компанія жодного разу не повторюється. Скількома способами це можна зробити?

2. Скількома способами із колоди у 36 карт можна витягнути 5 карт, серед яких 2 з однаковими номерами та 2 з однаковими, але іншими номерами?

3. Із двох спортивних суспільств, в яких тренується по 100 фехтувальників, треба виділити по одному фехтувальникові для участі в змаганні. Скількома способами може бути зроблений цей вибір?

4. У святах беруть участь 12 дітей. У діда Морозу є 15 однакових подарунків. Скільки існує способів роздати дітям подарунки, якщо кожна дитина має отримати, хоча б по одному дарунку?

5. Скількома способами можна посадити поруч 3 англійців, 3 французів та 3 турок так, щоб жодні три співвітчизники не сиділи поруч?

 

Варіант №2.

1.Скільки можна зробити перестановок із n елементів, в яких задані два елементи а і b не стоять поряд? Задані три елементи а, b, с не стоять поряд?

2.Десять крісел поставлено в ряд. Скількома способами на них можуть сісти два чоловіка? Скількома способами ці два чоловіки можуть сісти поруч? Скількома способами вони можуть сісти в ряд так, щоб між ними було, принаймні, одне крісло?

3.У селищі проживає 2000 мешканців. Довести, що, принаймні, два з них мають однакові ініціали?

4.Скількома способами 12 полтинників можна розкласти по 5 різним пакетам, якщо жоден з пакетів не може бути порожнім? 

5.На заміську прогулянку поїхали 92 чоловік. Бутерброди з ковбасою узяли 47 чоловік, з сиром – 38 чоловік, з шинкою – 42 людини, і з сиром і з ковбасою – 28 чоловік, і з ковбасою і з шинкою – 31 людина, і з сиром і з шинкою – 26 чоловік. Всі три види бутербродів узяли 25 чоловік, а декілька чоловік замість бутербродів захопили з собою пиріжки. Скільки чоловік узяли з собою пиріжки?

 

Варіант №3.

1.У автомашині сім місць. Скількома способами можуть 7 чоловік всістися в машину, якщо місце водія можуть зайняти тільки троє з них?

2.Скільки різних 10-значних чисел можна отримати, використовуючи в їх написанні цифри 2233344455?

3 .Четверо студентів складають іспит. Скількома способами їм можуть бути поставлені відмітки, якщо відомо, що ніхто з них не отримав не задовільної оцінки?

4. Скількома способами 10 полтинників можна розкласти по 4 різним пакетам, якщо пакети можуть бути порожніми?

5. Палітурник повинен переплести 12 різних книг в червону, зелену і коричневу палітурки. Скількома способами він може це зробити, якщо в кожен колір має бути переплетена, хоч би одна книга?

 

Варіант №4.

1.Скільки різних перестановок можна утворити зі всіх букв слова «добрива», якщо всі голосні повинні йти один за одним в наступному порядку «о, и, а»?

2. Вісім чоловік повинні розташуватися в двох кімнатах, причому, в кожній повинно бути, принаймні, 3 людини. Скількома способами вони можуть це зробити?

3. Скількома способами можна розкласти в дві кишені дев'ять монет різної гідності?

4. Троє хлопців зібрали з яблуні 40 яблук. Скількома способами вони можуть їх розділити, якщо всі яблука вважаються однаковими?

5. У черзі за морозивом стоять 5 хлопців. Скількома способами можна переставити хлопців так, щоб попереду кожного із них опинився інший, ніж був раніше?

 

Варіант №5.

1.У батька є 5 різних апельсинів, які він видає восьми своїм синам так, що кожен отримує або 1 апельсин, або нічого. Скількома способами можна це зробити?

2. З групи в 20 солдатів щоночі виділяються чергові із 3 чоловік. Скільки ночей підряд командир може виділяти таку трійку чергових, що не співпадає ні з однією із попередніх? Скільки разів при цьому буде чергувати якийсь певний солдат?

3. Скільки існує п'ятизначних чисел? У скількох з них всі цифри парні? У скільки не входять цифри, менші, ніж 6?

4. Скількома способами можна розставити 12 книжок в шафі з 5 полицями, якщо кожна полиця може вміщати все 12 книжок?

5. На каруселі катаються 5 хлопців. Вони вирішили пересісти так, щоб попереду кожного опинився інший, ніж був раніше. Скількома способами вони можуть це зробити?

 

Варіант №6.

1.Скількома способами можна розподілити 15 різних предметів між трьома особами, якщо перший повинен отримати 2 предмети, другий – 3 предмети і третій – 10 предметів?

2.Скільки способів розкласти в ряд 5 червоних м'ячів, 4 чорних, 5 білих м'ячів так, щоб м'ячі, лежачі на краях були одного кольору?

3. Скільки можна побудувати різних прямокутних паралелепіпедів, довжина кожного ребра яких є цілим числом від 1 до 100?

4. Скількома способами розділити 20 букв на 5 слів, якщо ніяке слово не може бути порожнім. Лад слів не має значення.

5. Знайти число перестановок з n елементів при яких m елементів не коштують на своїх місцях?

 

Варіант №7.

1. У залізничному вагоні 10 місць розташовано по ходу поїзда і 10 місць проти ходу поїзда. Скількома способами можна посадити у вагон 8 пасажирів, якщо два відмовляються сидіти по ходу поїзда, а три проти ходу поїзда?

2. Знайти число всіх можливих перестановок букв слова «зоологія». Скільки серед них таких, в яких 3 букви «о» стоять поряд? Скільки серед них таких, в яких у точності 2 букви «о» стоять поряд?

3. Кидають 7 гральних кісток. Скільки може вийти різних результатів, якщо на кожній кісті нанесені 1,2,3,4,5,6 очок і результати, що відрізняються лише порядком очок, вважаються однаковими?

4. Скільки чотиризначних чисел можна скласти з цифр від 0 до 5, якщо кожна цифра може повторюватися?

5. До обіду за круглим столом запрошені n пара ворогуючих лицарів (n≥2). Скільки існує способів розсадити їх так щоб жодні вороги не сиділи поруч?

 

Варіант №8.

1. У філателіста 8 різних канадських марок і 10 американських. Скількома способами він може відібрати 3 канадських і 3 американських марки і наклеїти їх в альбом на 6 пронумерованих місць?

2. Симфонія записана на 4 пластинках, причому для запису використовувалися обидві сторони кожної пластинки. Скільки існує способів програти цю симфонію так, щоб, принаймні, одна її частина потрапила не на своє місце?

3. Скількома способами можна розподілити 6 різних ящиків на 8 поверхів, щоб на восьмому поверсі були не менше двох ящиків?

4. Скількома способами 3 людини можуть розподілити між собою 6 однакових яблук, 1 апельсин, 1 сливу, 1 фінік, 1 лимон, 1 айву і 1 грушу?

5. Вісім чоловік стоять в черзі до театральної каси. Скількома способами їх можна переставити так, щоб попереду кожного з них йшов інший, ніж раніше?

 

Варіант №9.

1. Хтось має 8 різних пар рукавичок. Скількома способами він може відібрати одну рукавичку для правої руки і одну рукавичку для лівої, щоб вони не належали одній парі?

2. Протягом 10 тижнів студенти складають 10 іспитів, у тому числі 2 по математиці. Скількома способами можна розподілити іспити так, щоб екзамени з математики не слідували один за іншим?

3. Десять пасажирів їдуть в поїзді, який проходить через 5 населених пунктів. Скількома способами можуть розподілитися пасажири по зупинках, якщо кожен може вийти на будь-якій зупинці?

4. У перукарні 6 майстрів, скількома способами можуть обслужити 11 клієнтів, якщо кожен з майстрів повинен обслужити, хоч би одного клієнта?

5. Дівчина квапиться на побачення. Вона написала 5 листів, кожний із них адресовано одному з п'яти різних адресатів. Скількома способами можна здійснити розсилку листів так, що жоден із листів не потрапить за призначенням?

 

Варіант №10.

1. Скількома способами можна розставити на полиці сім книжок, якщо дві певні книги повинні стояти поряд; ці дві книги не повинні стояти поряд?

2. Пасажирський поїзд складається з двох багажних вагонів, чотирьох плацкартних і трьох купейних. Скількома способами можна сформувати поїзд, якщо багажні вагони повинні знаходитися спочатку, а купейні – в кінці? Якщо вагони можуть слідувати у будь-якому порядку?

3. У деякій державі не було двох жителів з однаковим набором зубів. Яка може бути найбільша чисельність населення держави, якщо найбільше число зубів дорівнює 32?

4. Вступні іспити складають 20 чоловік, скількома способами вони можуть розподілитися по 4 аудиторіям, якщо місткість аудиторій не менше 4 чоловік?

5. У черзі на виконання розташовано 10 задач, скількома способами планувальник може їх переставити так щоб кожна задача вибиралася на обслуговування після іншої, не тієї, що раніше?

Варіант №11.

1. Скільки шестизначних чисел можна утворити з цифр від 1 до 9, якщо кожне число повинно складатися із 3 парних і 3 непарних цифр, причому жодна цифра не входить до числа більше одного разу?

2. Музичний концерт складається з трьох пісень і двох скрипкових п'єс. Скількома способами можна скласти програму концерту так, щоб він починався і закінчувався виконанням пісні, і щоб скрипкові п'єси не виконувалися підряд?

3. Виходячи з вагону, хтось виявив в кишені нікель, дайм, квотер, півдолара. Скількома способами він може дати «на чай» носильникові?

4. Скількома способами можна розподілити 15 однакових олівців між 4 клерками, якщо кожен повинен отримати не менше 3?

5. Хтось бажає послати своєму другу 8 різних фотографій. Скількома способами він може це зробити, використовуючи 5 конвертів? Порожні конверти посилати не можна.

 

Варіант №12.

1. З групи у 12 чоловік щодня протягом 6 днів вибирають 2-х чергових. Визначити кількість різних списків чергових, якщо кожен чергує рівно один раз?

2. Скількома способами можна переставити букви в слові «банкнота», щоб голосні букви стояли на своїх місцях; йшли в алфавітному порядку?

3. У пасажирському поїзді дев'ять вагонів. Скількома способами можна розсадити в поїзді чотирьох чоловік за умови, що всі вони поїдуть:

- в різних вагонах;

- в одному вагоні?

4. Скількома способами можна надіти п'ять різних кілець на пальці однієї руки, виключаючи великий палець?

5. Скільки невід’ємних цілих чисел, менших, ніж мільйон складається із усіх цифр 1,2,3,4?

 

Варіант №13.

1. Довести, що число трьохбуквених слів, які можна утворити з букв слова «гіпотенуза», дорівнює числу всіх можливих перестановок букв, які входять у слово «призма».

2. Скількома способами можна переставити букви в слові «кофеварка», щоб голосні букви стояли на своїх місцях?

3. Скільки існує п'ятизначних чисел? Скільки серед них таких, які починаються цифрою 4? Які не містять цифри 5? Які діляться на 5?

4. Скількома способами можуть розподілитися 5 екзаменаторів між 40 абітурієнтами, якщо кожен з них повинен прийняти не менше 5 чоловік?

5. Беруться перестановки 5 чисел 1,2,3,4,5. У скількох з них жодне число не стоїть на своєму місці?

 

Варіант №14.

1. Скількома способами можна переставити букви в слові «ананас», щоб голосні та приголосні букви чергувалися?

2. З групи, що складається з 7 чоловіків і 4 жінок, треба вибрати 6 осіб так, щоб серед них були не менше двох жінок. Скількома способами це можна зробити?

3. Скількома способами можна розподілити між двома продавцями 300 екземплярів однієї книги, 200 екземплярів іншої і 100 екземплярів третьої, якщо жоден продавець не може отримати всіх книг одразу?

4. Скількома способами можна розподілити повну колоду карт (52 карти) між шістьма гравцями так щоб кожен отримав мінімум 2 карти?

5. Клітини шахівниці розфарбовуються в 8 кольорів так, що в кожному горизонтальному ряду зустрічаються всі 8 кольорів, а в кожному вертикальному ряду не зустрічаються підряд дві клітки, забарвлені в той же самий колір. Скількома способами можливе таке забарвлення?

 

Варіант №15.

1. Скількома способами з колоди в 36 карт можна вибрати дві з однаковими номерами?

2. Скількома способами з 5 подружніх пар можна відібрати чотирьох чоловік, якщо:

- в число відібраних повинні входити двоє чоловіків і дві жінки;

- жодна подружня пара не повинна входити до цього числа.

3. На залізничній станції є m світлофорів. Скільки може бути дано різних сигналів, якщо кожен світлофор має три кольори: жовтий, зелений і червоний?

4. Скількома способами можна розподілити 15 чоловік 3 бригадам, якщо кожна з бригад виконує окремий вид робіт?

5. Два екзаменатори працюючи одночасно, іспитують клас в 12 чоловік по 2 предметам. Скількома способами можуть екзаменатори розподілити роботу між собою так, щоб жодному школяру не довелося відразу відповідати по двох предметах?

 

Варіант №16.

1. Скількома способами з колоди в 52 карти можна вибрати 2 з однаковими номерами і 3 з іншими однаковими між собою номерами?

2. У корзині лежать 12 яблук і 10 апельсинів. Один з братів вибирає з неї яблуко або апельсин, після чого другий брат бере і яблуко, і апельсин. У якому випадку другий брат має більшу свободу вибору: якщо перший брат узяв яблуко або якщо він узяв апельсин (апельсини і яблука різні)?

3. Треба послати 6 термінових листів. Скількома способами можна це зробити, якщо для передачі листів можна послати 3 кур'єри і кожен лист можна дати будь-якому з них?

4. Скількома способами можна розкласти у 9 луз 7 білих і 2 чорні кулі, якщо частина луз може бути порожньою, лузи вважаються різними?

5. Скількома способами можна переставити цифри числа 123512345 так, щоб дві однакові цифри не йшли одна за другою?

 

Варіант №17.

1. У мами 2 яблука і 3 груші. Щодня протягом п'яти днів підряд вона дає синові по одному фрукту. Скількома способами це може бути зроблено?

2. Скількома способами можна переставити букви слова «огород» так, що три букви «о» не стояли поряд?

3. Є 3 курки, 4 качки і 2 гусаки. Скільки існує комбінацій для вибору декількох птиць так, щоб серед вибраних птиць були і кури, і качки, і гусаки?

4. З колоди в 52 карти потрібно витягнути 6 карт. Скількома способами можна це зробити, якщо карта після витягування повертається в колоду; карта не повертається в колоду?

5. Скільки способами можна переставити букви слова «особенность» так, щоб дві однакові букви не йшли один за одним?

Варіант №18.

1. Скількома способами з колоди у 36 карт можна витягнути 5 карт, 3 з яких з однаковими номерами, а 2 – з різними?

2. У спортивному клубі тренуються 30 чоловік. Скількома способами можна скласти команду для участі в естафеті 100+200+400+800?

3. У англійців прийнято давати дітям декілька імен. Скількома способами можна назвати дитину, якщо загальне число імен дорівнює 300, а йому дають не більше 3 імен? (Назвати можна одним, двома і трьома іменами).

4. Скількома способами можна розкидати n однакових кульок по різних лузах, якщо лузи не можуть бути порожніми?

5. На полиці розташовано 4 книги О.С. Пушкіна, 2 книги Л.М. Толстого, 3 книги Ф.М. Достоєвського. Скількома способами можна переставити книги на полиці так, щоб книжки одного автору не стояли поряд?

 

Варіант №19.

1. Скількома способами з колоди у 36 карт можна витягти 5 карт із номерами, що йдуть підряд, та одного кольору?

2. Скількома способами можна переставити букви в слові «пастухи», так щоб між двома голосними були дві приголосні?

3. Двадцять чоловік голосують за шість різних кандидатів. Скількома способами можуть розподілитися голоси, якщо кожен проголосує рівно за одного кандидата і враховується, лише число голосів, поданих за кожного кандидата?

4. Скількома способами можна розкидати n однакових кульок за різними лузами, якщо деякі лузи можуть бути порожніми?

5. Скільки шестизначних чисел можна скласти з цифр числа 1233145254 так, щоб дві однакові цифри не йшли одна за другою?

 

Варіант №20.

1. Скількома способами із колоди у 36 карт можна витягти 5 карт однієї масті, з номерами що йдуть підряд?

2. Скількома способами можна переставити букви слова «фацетія» так, щоб не мінявся порядок голосних?

3. Скількома способами можна вибрати з 15 чоловік групу людей для роботи? У групу можуть входити 1, 2,…, 15 чоловік.

4. У конкурсі беруть участь 5 чоловік. Є 8 винагород різних рівнів. Скількома способами можна розподілити винагороди між учасниками конкурсу?

5. Скільки існує цілих чисел від 0 до 999, які не діляться ні на 2, ні на 3, ні на 5?

 

Варіант №21.

1. Скількома способами можна переставити букви в слові «логарифм», щоб голосні букви стояли на своїх місцях?

2. Скільки різних 4-хзначних чисел можна скласти з цифр 0,1,2,3,4,5, якщо кожна з них може повторитися кілька разів?

3. Скількома способами можна розбити n різних предметів на 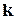 груп?

4. Скількома способами можна розкидати n різних кульок за 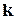 різними лузами, якщо лузи мають задану місткість ?

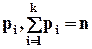5. Скільки існує цілих невід’ємних чисел від 0 до 999, які не діляться ні на 5, ні на 7?

 

Варіант №22.

1. Телефонні номери в деякому місті складаються із 7 цифр. Скільки номерів можна згенерувати, якщо цифри в номері можуть повторюватися і номер не може починатися з цифри «0» і «8»?

2. Скількома способами можна переставити букви в слові «пастухи» так, щоб як голосні, так і приголосні йшли в алфавітному порядку?

3. Скількома способами можна вибрати з колоди в 52 карти по одній карті кожної масті так, щоб карти червоних мастей і карти чорних мастей утворювали пари?

4. Скількома способами можна розкидати  різних куль по різним лузам, якщо місткість луз не обмежена та порядок попадання куль в лузу має значення?

5. Скількома способами можна переставити букви в слові «тартар», щоб однакові букви не йшли одна за одною?

 

Варіант №23.

1. Скількома способами можна вибрати з чисел натурального ряду від 1 до 30 три числа так, щоб їх сума була парною?

2. Скількома способами можна переставити букви в слові «самовар» так, щоб голосні та приголосні букви чергувалися?

3. Скількома способами з колоди в 52 карти можна вибрати по одній карті кожної масті?

4. Скількома способами можна розкидати n однакових куль до різних луз, якщо в кожній лузі повинно бути не менше, ніж l куля?

5. У групі 25 студентів. Мовою програмування С++ з них володіють 19 чоловік Паскалем – 12 чоловік, Асемблером – 8 чоловік; С++ та Паскалем володіють 10 чоловік, С++ та Асемблером – 7 чоловік, Паскалем та Асемблером – 6 чоловік. Усіма трьома приведеними мовами програмування володіють 5 чоловік. А декілька студентів не володіють жодною з цих мов програмування. Скільки таких студентів?

 

Варіант №24.

1. У футбольній команді грають – 13 польових гравців і 2 воротарі. Скільки способів вибрати граючий склад: 11– гравців, 1 – воротар?

2. Скількома способами можна переставити букви в слові «Абакан» так, щоб приголосні йшли в алфавітному порядку?

3. Сім дівчат водять хоровод. Скількома різними способами вони можуть встати у коло?

4. Скількома способами можна розкидати n різних куль до різних луз, якщо лузи не можуть бути порожніми і має значення порядок куль в лузі?

5. У відділі науково-дослідного інституту працюють декілька чоловік, причому кожен з них знає хоча б одну іноземну мову. 6 чоловік знають англійський, 6 – німецький, 7 – французький, 4 знають англійський і німецький, 3 – німецький і французький, 2 – французький і англійський. Одна людина знає всі три мови. Скільки чоловік працює у відділі? Скільки з них знають лише англійський? Лише французький?

 

Варіант №25.

1. Скількома способами з колоди в 36 карт можна витягнути 5 карт, серед яких 4 карти із однаковими номерами?

2. Скількома способами можна переставити букви в слові «молоко» так, щоб приголосні йшли в алфавітному порядку і дві букви «о» не йшли підряд?

3. У англійців прийнято давати дітям декілька імен. Скількома способами можна назвати дитяти, якщо спільне число імен дорівнює 300, а йому дають не більше 3 імен? Імена можуть повторюватися.

4. Скількома способами можна розкидати  різних куль у 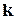 різних луз якщо деякі лузи можуть бути порожніми і не має значення порядок куль в лузі?

5. По пустелі йде караван з 7 верблюдів. Подорож триває багато днів і, нарешті, всім набридає бачити попереду себе одного і того ж верблюда. Скількома способами можна переставити верблюдів так щоб попереду кожного верблюда йшов інший, чим раніше?

Варіант №26.

1. Скількома способами можна розсадити 10 гостей за круглим столом?

2. Скількома способами з колоди в 36 карт можна витягнути 5 карт, серед яких 4 з однаковими номерами?

3.Скільки цілих позитивних вирішень має рівняння:

?

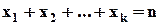4. У рамку проектору одночасно вставляють чотири діапозитиви, які проектуються на 4 екрани. При цьому кожен діапозитив можна поставити 4 способами, і лише один з них є вірним. Скільки існує способів поставити діапозитиви так, щоб, принаймні один з них не було поставлено вірно?

5. Кожен учень класу або дівчинка, або має світле волосся, або любить математику. У класі 20 дівчаток, з них 12 блондинок, і одна блондинка любить математику. Всього в класі 24 учня є блондинами, математику з них люблять 12, а всього учнів, які люблять математику, 17; із них 6 дівчаток. Скільки учнів в даному класі?

 

Варіант №27.

1. Скількома способами з колоди в 53 карти можна витягнути 5 карт, серед яких 5 із однаковими номерами, причому в ролі джокера виступає додаткова карта?

2. На зборах повинні виступити 4 людини. Скількома способами їх можна розмістити в списку ораторів, якщо B не може виступити до того моменту, поки не виступить A?

3. Скількома способами можна розподілити 18 солдатів по 5 казармам, якщо має значення лише, скільки солдатів потрапило в яку казарму, і в кожній з казарм не може бути менше, ніж  2 солдатів?

4. При передачі повідомлень телеграфом застосовується код Морзе. У цьому коді використовуються символи: крапка і тире. Якої довжини мають бути коди для букв російського алфавіту?

5. На екскурсії були учні сьомих та восьмих класів. Всі вони були або з комсомольськими значками, або в піонерських галстуках. Хлопчиків було 16, а комсомольців – 24. Піонерок було рівно стільки, скільки хлопчиків-комсомольців. Скільки учнів було на екскурсії?

 

Варіант №28.

1. Маємо p білих і q чорних куль. Скількома способами можна викласти в ряд всі кулі так, щоб жодні 2 чорні кулі не лежали поруч?

2. Скількома способами з колоди в 36 карт можна витягнути 5 карт, серед яких 5 з однаковими номерами, причому сімка пікової масті виступає в ролі джокера?

3. Скільки цілих невід’ємних вирішень має нерівність:

?

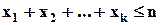4. Є n однакових куль і ще n різних куль. Скількома способами з них можна вибрати n куль? Скількома способами можна упорядкувати всі кулі?

5. У класі вчаться 35 учнів. З них 20 відвідує математичний кружок, 11 – фізичний 10 учнів не відвідують жодного з цих кружків. Скільки учнів відвідують і математичний, і фізичний кружок? Скільки учнів відвідують лише математичний кружок?

 

Варіант №29.

1. Скількома способами можна переставити букви в слові «паралелізм» так, щоб не змінювався лад голосних?

2. Скількома способами з колоди в 36 карт можна витягнути 5 карт, серед яких 4 з однаковими номерами?

3. Скільки можна зробити кісток доміно, використовуючи числа 0,1,…,r?

4. Скільки шестизначних чисел містять рівно 3 різних цифри?

5. Використовуючи метод включення і виключення, знайти число способів розміщення r різних предметів в n луз, причому не може бути порожніх луз?

 

Варіант №30.

1. Пасажир залишив речі в автоматичній камері схову, а коли прийшов отримувати речі, з'ясувалося, що він забув номер. Він лише пам'ятає, що в номері були числа 26 і 37. Щоб відкрити камеру, потрібно правильно вибрати п'ятизначний номер. Яку найбільшу кількість номерів потрібно перебрати щоб відкрити камеру?

2. Скількома способами з колоди в 37 карт (36 карт плюс джокер) можна витягнути 5 карт, серед яких 5 з однаковими номерами?

3. У поштовому відділенні продаються листівки 10 сортів. Скільки існує способів купити 8 листівок? 8 різних листівок? 12 листівок?

4. Є 14 пар різних предметів. Знайти повне число вибірок з цих предметів, причому вибірки повинні відрізнятися, лише складом елементів, але не їх порядком.

5. Використовуючи метод включення і виключення, знайти число способів розміщення r різних предметів в n луз, причому рівно m луз є порожніми?

Література

 

1.  Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969. – 328 с.

2. Андерсон Дж. Дискретная математика и комбинаторика. – М.: Мир, 2001. – 960 с.

3. Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики. – М.: Наука, 1977. – 80 с.

4. Глускин Л.М., Шварц В.Я., Шор Л.А. Задачи и алгоритмы комбинаторики и теории графов. – Донецк: ДПИ,1982. – 112 с.

5. Липский В. Комбинаторика для программистов. – М.: Мир, 1988.

6. Риордан Д. Введение в комбинаторный анализ.– М.: ИЛ, 1963.– 288с.

7. Холл М. Комбинаторика. – М.: Мир, 1970. – 424с.

 

 

 

Навчальне видання

 

 

Методичні вказівки та завдання до індивідуальної роботи за курсом

"Топологія економічних структур"

(для студентів, що навчаються за напрямком підготовки

"Економічна кібернетика")