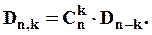| З’єднання
| Без повторен ь
елемент ів
| З повторен нями
елемент ів
|
| Перестановки
| 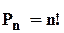
| 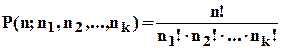
|
| Розміщення
| 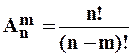
| 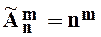
|
| Сполучення
| 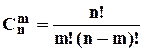
| 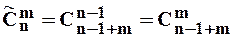
|
Тема№3
Принцип включення-виключення
Нехай є деяка скінченна множина 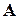 , що має потужність у
, що має потужність у 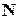 об'єктів та множина властивостей
об'єктів та множина властивостей 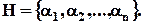 Кожний об'єкт множини
Кожний об'єкт множини 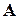 може володіти або не володіти однією або одночасно декількома (всіма) властивостями із множини
може володіти або не володіти однією або одночасно декількома (всіма) властивостями із множини 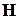 .
.
Введемо ряд позначень.
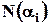 – кількість об'єктів множини
– кількість об'єктів множини 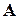 , які володіють властивістю
, які володіють властивістю 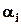 ;
;
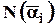 – кількість об'єктів, що не володіють властивістю
– кількість об'єктів, що не володіють властивістю 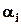 ;
;
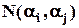 – кількість об'єктів, що володіють двома властивостями
– кількість об'єктів, що володіють двома властивостями 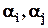 одночасно;
одночасно;
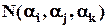 – кількість об'єктів, що володіють трьома властивостями
– кількість об'єктів, що володіють трьома властивостями 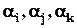 одночасно;
одночасно;
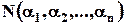 – кількість об'єктів, що володіють усіма
– кількість об'єктів, що володіють усіма  властивостями множини
властивостями множини 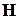 одночасно;
одночасно;
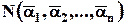 – кількість об'єктів, що не володіють ні одним з
– кількість об'єктів, що не володіють ні одним з  властивостей множини
властивостей множини 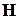 .
.
Теорема 4

Доведення.
Формула включень та виключень визначає кількість об'єктів, що не володіють ні однією з властивостей, заданих множиною 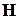 .
.
Наприклад:
На фірмі працює 67 співробітників. З них 47 володіють англійською мовою, 35 – німецькою, 20 – французькою; одночасно англійською та німецькою володіють – 23 співробітника, англійською та французькою – 12, німецькою та французькою – 11, трьома мовами володіють 5 співробітників. Скільки співробітників не володіють ні однією із перерахованих мов?
Розв’язання.
Визначимо наступні властивості:
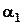 – "володіти англійською мовою”;
– "володіти англійською мовою”;
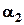 – "володіти німецькою мовою;
– "володіти німецькою мовою;
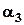 – "володіти французькою мовою".
– "володіти французькою мовою".
За формулою включень і виключень маємо:
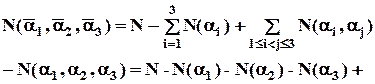
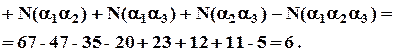
Окремі випадки формули включень і виключень
1. Якщо всі властивості 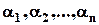 попарно несумісні, тобто
попарно несумісні, тобто
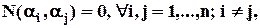
то формула включень і виключень має вигляд:
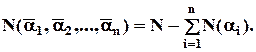
2. Якщо кожне число 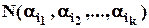 залежить не від характеру властивостей, а лише від їх кількості, то формула має вигляд:
залежить не від характеру властивостей, а лише від їх кількості, то формула має вигляд:
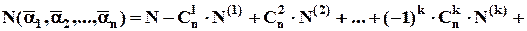
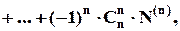
де 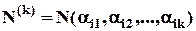 – кількість об’єктів, що володіють рівно
– кількість об’єктів, що володіють рівно 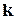 властивостями.
властивостями.
Зада ча про безлад
Нехай є множина 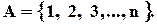
Розглянемо перестановки елементів множини 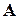 .
.
Елемент перестановки називається нерухомим, якщо 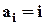 , тобто елемент стоїть на своєму місці.
, тобто елемент стоїть на своєму місці.
Наприклад.
При 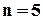 у перестановці
у перестановці 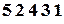 – елемент
– елемент 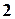 – нерухомий, а у перестановці
– нерухомий, а у перестановці 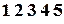 – усі елементи нерухомі.
– усі елементи нерухомі.
Безладом називається перестановка, яка не має нерухомих елементів, тобто 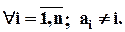
Постановка за дачі
Визначити 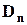 – кількість безладів у
– кількість безладів у  -елементній множині, або кількість перестановок чисел
-елементній множині, або кількість перестановок чисел 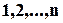 таких, що
таких, що 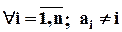 .
.
Розв’язання.
Загальне число перестановок у  -елементній множині дорівнює
-елементній множині дорівнює 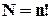 . Позначимо через
. Позначимо через 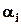 таку властивість перестановки, що
таку властивість перестановки, що 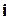 -й елемент стоїть на своєму місці, тобто
-й елемент стоїть на своєму місці, тобто 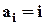 . Тоді ліва частина формули включень та виключень
. Тоді ліва частина формули включень та виключень 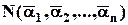 і є розв’язком задачі про безлад. За позначенням
і є розв’язком задачі про безлад. За позначенням 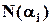 є кількість перестановок в
є кількість перестановок в  -елементній множині, у яких один
-елементній множині, у яких один 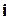 -тий елемент стоїть на своєму місці і дорівнює
-тий елемент стоїть на своєму місці і дорівнює 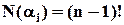 , бо один елемент не можна переставляти, а останні елементи можуть бути переставлені
, бо один елемент не можна переставляти, а останні елементи можуть бути переставлені 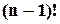 способами. Так як число перестановок не залежить від того, який саме елемент знаходиться на своєму місці, то:
способами. Так як число перестановок не залежить від того, який саме елемент знаходиться на своєму місці, то:
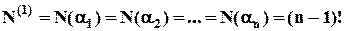 :
:
Аналогічно, визначимо 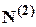 – кількість перестановок, у яких рівно два елементи знаходяться на своїх місцях:
– кількість перестановок, у яких рівно два елементи знаходяться на своїх місцях: 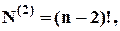 та, відповідно,
та, відповідно, 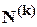 – кількість перестановок, у яких тільки
– кількість перестановок, у яких тільки 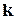 елементів знаходяться на своїх місцях:
елементів знаходяться на своїх місцях: 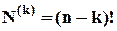 .
.
За формулою включень-виключень маємо:
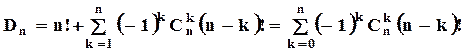
Розпишемо формулу
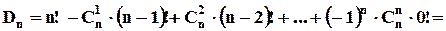
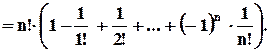
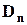 – ще називають субфакторіалом.
– ще називають субфакторіалом.
Зада ча про зустріч
Визначити кількість таких перестановок чисел 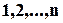 , що точно
, що точно 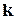 елементів із
елементів із  знаходяться на своїх місцях (тобто
знаходяться на своїх місцях (тобто 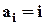 ), а інші
), а інші  , перебувають у безладі.
, перебувають у безладі.
Інакше: нас цікавлять перестановки, в яких рівно 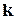 елементів нерухомі.
елементів нерухомі.
Розв’язання.
Із загального числа елементів вибирається 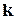 , які залишаються на своїх місцях. Оскільки вибір елементу визначає й його місце розташування, то кількість варіантів дорівнює:
, які залишаються на своїх місцях. Оскільки вибір елементу визначає й його місце розташування, то кількість варіантів дорівнює: 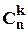 . Для інших
. Для інших  елементів розв’язується задача про безлад:
елементів розв’язується задача про безлад: 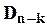 . Тоді,за правилом добутку кількість способів, якими можна переставити
. Тоді,за правилом добутку кількість способів, якими можна переставити  елементів при таких умовах, дорівнює:
елементів при таких умовах, дорівнює:
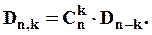





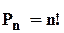
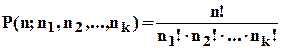
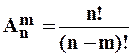
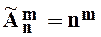
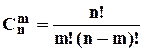
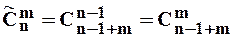
 , що має потужність у
, що має потужність у 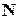 об'єктів та множина властивостей
об'єктів та множина властивостей 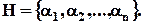 Кожний об'єкт множини
Кожний об'єкт множини 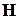 .
.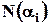 – кількість об'єктів множини
– кількість об'єктів множини 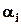 ;
;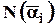 – кількість об'єктів, що не володіють властивістю
– кількість об'єктів, що не володіють властивістю 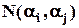 – кількість об'єктів, що володіють двома властивостями
– кількість об'єктів, що володіють двома властивостями 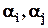 одночасно;
одночасно;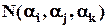 – кількість об'єктів, що володіють трьома властивостями
– кількість об'єктів, що володіють трьома властивостями 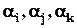 одночасно;
одночасно;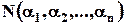 – кількість об'єктів, що володіють усіма
– кількість об'єктів, що володіють усіма  властивостями множини
властивостями множини 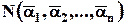 – кількість об'єктів, що не володіють ні одним з
– кількість об'єктів, що не володіють ні одним з 
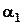 – "володіти англійською мовою”;
– "володіти англійською мовою”;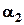 – "володіти німецькою мовою;
– "володіти німецькою мовою;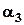 – "володіти французькою мовою".
– "володіти французькою мовою".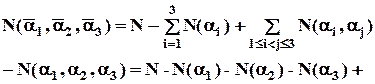
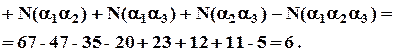
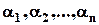 попарно несумісні, тобто
попарно несумісні, тобто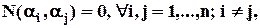
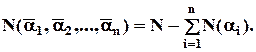
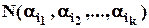 залежить не від характеру властивостей, а лише від їх кількості, то формула має вигляд:
залежить не від характеру властивостей, а лише від їх кількості, то формула має вигляд: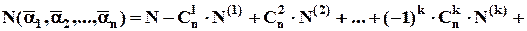
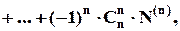
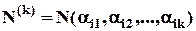 – кількість об’єктів, що володіють рівно
– кількість об’єктів, що володіють рівно 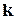 властивостями.
властивостями.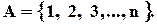
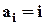 , тобто елемент стоїть на своєму місці.
, тобто елемент стоїть на своєму місці.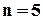 у перестановці
у перестановці 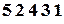 – елемент
– елемент 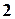 – нерухомий, а у перестановці
– нерухомий, а у перестановці 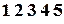 – усі елементи нерухомі.
– усі елементи нерухомі.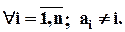
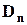 – кількість безладів у
– кількість безладів у 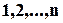 таких, що
таких, що 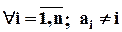 .
.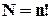 . Позначимо через
. Позначимо через 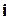 -й елемент стоїть на своєму місці, тобто
-й елемент стоїть на своєму місці, тобто 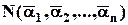 і є розв’язком задачі про безлад. За позначенням
і є розв’язком задачі про безлад. За позначенням 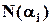 є кількість перестановок в
є кількість перестановок в 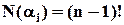 , бо один елемент не можна переставляти, а останні елементи можуть бути переставлені
, бо один елемент не можна переставляти, а останні елементи можуть бути переставлені 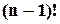 способами. Так як число перестановок не залежить від того, який саме елемент знаходиться на своєму місці, то:
способами. Так як число перестановок не залежить від того, який саме елемент знаходиться на своєму місці, то: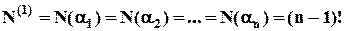 :
: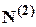 – кількість перестановок, у яких рівно два елементи знаходяться на своїх місцях:
– кількість перестановок, у яких рівно два елементи знаходяться на своїх місцях: 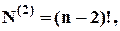 та, відповідно,
та, відповідно, 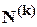 – кількість перестановок, у яких тільки
– кількість перестановок, у яких тільки 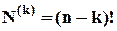 .
.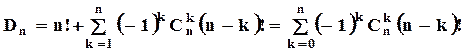
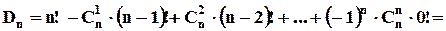
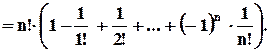
 , перебувають у безладі.
, перебувають у безладі.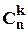 . Для інших
. Для інших 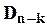 . Тоді,за правилом добутку кількість способів, якими можна переставити
. Тоді,за правилом добутку кількість способів, якими можна переставити