Линейным чирпом
В работах двух последних десятилетий неоднократно сообщалось об использовании диспергирующих сред в качестве средства для эффективного сжатия импульсов. В частности, оптическое волокно в сочетании с парой дифракционных решеток, а в ряде случаев и без них, позволяет во много раз сжимать лазерные импульсы, в отдельных случаях доводя их длительность до величины, не превосходящей 10 фемтосекунд, то есть до нескольких периодов оптических колебаний. В настоящее время дисперсионные явления представляют собой наиболее эффективный способ управляемого и контролируемого воздействия на параметры сверхкоротких лазерных импульсов.
Сущность явлений дисперсионного уширения и сжатия сигналов проще всего проиллюстрировать на примере импульса гауссовой формы. После прохождения слоя диспергирующей среды огибающая импульса приобретает фазовый сдвиг, временная зависимость которого носит нелинейный характер. Производную этого фазового сдвига естественно трактовать как смещение мгновенной частоты сигнала D w относительно оптической несущей w 0. Для импульса гауссовой формы результат оказывается чрезвычайно простым

то есть в области нормальной дисперсии сдвиг частоты положителен на заднем фронте и отрицателен на переднем фронте импульса.
Обратимся теперь к введённому ранее понятию «групповой» скорости
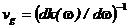 . Считая vg функцией частоты, вычислим приращение этой функции в окрестности точки w 0
. Считая vg функцией частоты, вычислим приращение этой функции в окрестности точки w 0

Если теперь трактовать vg как скорость переноса энергии одной, отдельно взятой, монохроматической компонентой волнового пакета, то в области нормальной дисперсии, т. е. при выполнении условия k ²0 > 0, положительным значениям D w; ставятся в соответствие отрицательные значения D vg, и наоборот. Другими словами, дисперсионное уширение обусловлено постепенным, но неуклонным отставанием задних компонент импульса от передних по мере его распространения.
Для реализации сценария, при котором имеет место сжатие сигнала, следует изменить начальные условия. Зная, что дисперсионные эффекты ускоряют передний фронт импульса и притормаживают задний, необходимо добавить к огибающей входного сигнала компенсирующий фазовый сдвиг, который бы искусственно замедлял скорость распространения передней части импульса и увеличивал скорость «хвостовой» части импульса. В результате, на начальной стадии эволюции сигнала будет происходить наложение задних компонент волнового пакета на передние, что внешне должно проявляться как сжатие импульса во временной области с соответствующим ростом его интенсивности.
Наибольшее сокращение длительности произойдёт при такой длине среды, когда порождённый дисперсией фазовый сдвиг будет полностью компенсировать фазовый сдвиг исходного импульса. Поскольку в рамках принятого нами приближения (5.3) любая дисперсионная среда выступает в качестве источника линейного чирпа, то полная компенсация фазовых сдвигов, и следовательно, максимально возможное сжатие, возникает только в том случае, если чирп исходного сигнала также является линейным. В остальных случаях нелинейного чирпа может иметь место уменьшение степени сжатия сигнала или даже расслоение одиночного импульса на несколько подимпульсов.
Перейдём к количественному описанию рассматриваемых явлений, начав, как и ранее, с простейшей модели гауссова импульса с линейным чирпом. Огибающая импульса уже на входе в среду представляется комплексной функцией
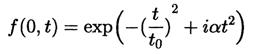
с вещественным параметром a, характеризующим скорость чирпа. Знак этого параметра определяет направление сдвига несущей частоты, поскольку D w (t) = 2 a t. Фурье-образ огибающей сигнала
-также комплексный, причём измеряемая в эксперименте интенсивность спектра Is (w), с точностью до нормировочного множителя равная величине

оказывается уширенной вследствие фазовой модуляции.
Вводя безразмерную скорость чирпа ` a = a t 0 2 и подставляя найденную зависимость x (w) в (5.3), представим амплитуду сигнала на расстоянии L в виде

Вычисляя данный интеграл аналогично (5.5), получаем явное выражение для комплексной огибающей

которое удобно привести к экспоненциальному виду, выделив результирующий фазовый сдвиг j (m, 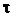 ) в виде отдельного сомножителя
) в виде отдельного сомножителя
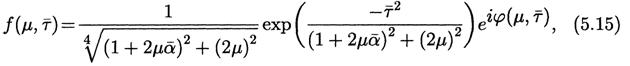
где
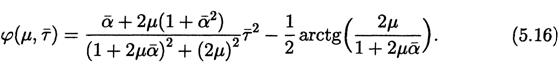
Таким образом, распространяющийся в дисперсионной среде гауссов импульс даже при наличии линейного чирпа сохраняет свою функциональную форму. Однако теперь его длительность зависит от пройденного расстояния более сложным образом. Относительное уширение импульса находится непосредственно из выражения (5.15), что с учётом (5.6) даёт

Из (5.17) видно, что на больших длинах длительность импульса, прошедшего слой среды толщиной L, остаётся пропорциональной пройденному пути. Действительно, при L ® ¥, что эквивалентно m ® ¥,
то есть введение чирпа в исходный импульс ускоряет его дисперсионное расплывание на больших длинах по отношению к такому же импульсу без чирпа. Данный эффект хорошо заметен на рис.5.6а, где относительное уширение импульса без чирпа показано более толстой линией.
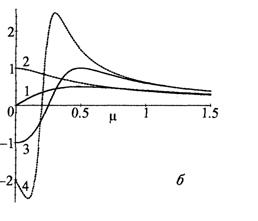
Рис.8.4. а) Относительное уширение гауссова импульса с линейным чирпом, 6) квадратичный по  коэффициент функции фазового сдвига j(m,
коэффициент функции фазового сдвига j(m,  ) из (5.16). Значения величины скорости чирпа: кривая 1 -
) из (5.16). Значения величины скорости чирпа: кривая 1 -  = 0, 2 -
= 0, 2 -  = 1, 3 -
= 1, 3 -  = -1, 4 -
= -1, 4 -  = -2.
= -2.
Минимизируя подкоренное выражение в (5.17) можно получить значение параметра m, при котором произойдет максимальное сжатие сигнала

Соотношение (5.18) можно получить и непосредственно из анализа функции фазового сдвига j(m, 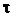 ). Поскольку после прохождения слоя среды чирп продолжает оставаться линейным, то начальной фазе сжатия импульса будут, как показано на рис.8.4б, соответствовать отрицательные значения квадратичного по
). Поскольку после прохождения слоя среды чирп продолжает оставаться линейным, то начальной фазе сжатия импульса будут, как показано на рис.8.4б, соответствовать отрицательные значения квадратичного по 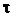 коэффициента функции j(m,
коэффициента функции j(m, 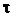 ). Максимальное сжатие, как уже отмечалось ранее, достигается при полной компенсации дисперсионных искажений чирпом исходного сигнала. Приравнивая нулю коэффициент при
). Максимальное сжатие, как уже отмечалось ранее, достигается при полной компенсации дисперсионных искажений чирпом исходного сигнала. Приравнивая нулю коэффициент при 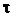 2 в (5.16) и решая получившееся линейное уравнение, сразу же получаем (5.18).
2 в (5.16) и решая получившееся линейное уравнение, сразу же получаем (5.18).
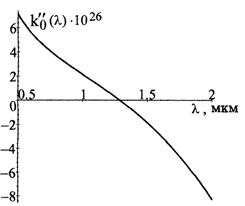
Из выражения для mmin следует, что в области нормальной дисперсии при положительном значении  мы имеем дело с монотонным уширением импульса (кривые 2 на рис.8.4а и 8.46»). Для большинства оптически прозрачных сред при отсутствии примесей, способных создавать ярко выраженные полосы резонансного поглощения, область видимого диапазона как раз и является областью нормальной дисперсии. Если от частоты w перейти к более привычной единице измерения - длине волны l, то величина k 0 ² находится из следующего простого соотношения:
мы имеем дело с монотонным уширением импульса (кривые 2 на рис.8.4а и 8.46»). Для большинства оптически прозрачных сред при отсутствии примесей, способных создавать ярко выраженные полосы резонансного поглощения, область видимого диапазона как раз и является областью нормальной дисперсии. Если от частоты w перейти к более привычной единице измерения - длине волны l, то величина k 0 ² находится из следующего простого соотношения:
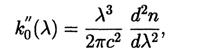
то есть имеет тот же знак, что и вторая производная показателя преломления. Для аналитического представления спектральной зависимости показателя преломления часто используют интерполяционные формулы, которые по своей структуре совпадают с известной формулой Зельмейера. Если учесть, что каждый резонансный контур характеризуется лишь двумя независимыми параметрами, то для точного описания зависимости n(l) обычно приходится модифицировать классическую формулу, добавляя в неё дополнительные резонансные области - реальные или виртуальные. Для химически чистого плавленного кварца приводится следующий пример такого трёхчленного соотношения[8]:

На протяжении всей главы, иллюстрируя те или иные закономерности, нам придётся часто восстанавливать истинные значения физических величин, исходя из известной величины безразмерного параметра m. Так как в качестве стандартной модельной среды нами будут рассматриваться оптические волокна на основе кварцевого стекла, то имеет смысл привести здесь конкретные значения параметров Bj и lj:
 B 1 = 0.6961663 l12 = 0.004679148 мкм2,
B 1 = 0.6961663 l12 = 0.004679148 мкм2,
B 2 = 0.4079426 l22 = 0.01351206 мкм2,
B 3 = 0.8974994 l32 = 97.934002 мкм2.
| Рис.8.5. Спектральная зависимость дисперсионного параметра второго порядка для плавленного кварца. Размерность данных по вертикальной оси: с2/м.
|
О масштабе величины дисперсионного параметра можно судить хотя бы по тому, что на длине волны l =0.7 мкм, значение k0² оказывается равным 4.5 10-26 с2/м. Результата вычислений по вышеуказанным формулам позволяют можно получить зависимость, показанную на рис.5.7. Откуда, в частности, следует, что величина k 0 ² оказывается положительной, если длина волны не превышает 1.27 мкм. Следовательно, фаза сжатия реализуется только для таких импульсов, у которых частота уменьшается от начала к концу по линейному закону. При этом существует единственное значение длины Lmin, вычисляемое из соответствующего значения m min, на которой длительность импульса становится минимальной и равной

Поскольку выражение (5.19) не зависит от величины k 0 ², то предельная длительность, до которой может быть сжат импульс, также не зависит от свойств среды, а определяется только длительностью входного сигнала и скоростью чирпа. Фазовый сдвиг в состоянии максимального сжатия полностью скомпенсирован; следовательно, такой импульс будет спектрально-ограниченным. При этом переход через точку максимального сжатия сопровождается изменением знака у квадратичного по 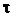 коэффициента функции j (m,
коэффициента функции j (m, 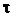 )(кривые 3, 4 рис.8.4б ).
)(кривые 3, 4 рис.8.4б ).
Так как в рамках рассматриваемой модели среда не вносит потерь, то сжатие импульса должно сопровождаться ростом его пиковой мощности. На длине Lmin максимальная интенсивность излучения возрастает в  раз по сравнению с исходной. Это обстоятельство следует принимать во внимание при определении коэффициента затухания оптического волокна импульсными методами.
раз по сравнению с исходной. Это обстоятельство следует принимать во внимание при определении коэффициента затухания оптического волокна импульсными методами.
Анализируя зависимость параметра m min от величины чирпа в (5.18), нетрудно заметить, что m min < 1/4 для любых отрицательных значений  , причем максимум достигается при
, причем максимум достигается при  =- 1. Другими словами, фаза сжатия исходного импульса всегда является начальной стадией его эволюции независимо от скорости чирпа, так как m min ® 0 как при
=- 1. Другими словами, фаза сжатия исходного импульса всегда является начальной стадией его эволюции независимо от скорости чирпа, так как m min ® 0 как при  ® 0, так и при
® 0, так и при  ® - ¥.
® - ¥.
Проиллюстрируем найденные закономерности на конкретных примерах. Начнём с импульсов гауссовой формы наносекундной длительности, Полагая t p0 равным 10-9 с, найдем величину масштабного множителя t0 из условия (5.6), что даёт значение 0.85 10-9 с. Линейный сдвиг частоты Dn за время импульса t p0 примем равным 108Гц. Тогда из соотношения Dw = 2a t p0 можно рассчитать значение параметра a, фигурирующего в расчётных формулах

Подставляя значение  в (5.19), находим минимальную длительность импульса t pmin» 0.975 10-9 с. На длине волны l = 0.7мкм, сдвиг частоты
в (5.19), находим минимальную длительность импульса t pmin» 0.975 10-9 с. На длине волны l = 0.7мкм, сдвиг частоты
Dn = 108 Гц соответствует смещению длины волны Dl»1.6 10-3 Å, а значение Lmin восстановленное из показанной на рис.5.7 зависимости k 0 ²(l) и величины m min оценивается в 1700 км.
Использованные в данном примере численные значения параметров исходного сигнала являются достаточно типичными для многих встречающихся на практике ситуаций. Соответствующее этим параметрам t p0 и Dn значение величины |a| оказывается значительно меньше 1, т. е. в динамике распространения таких импульсов, отсутствуют ярко выраженные эффекты, обусловленные наличием чирпа. Для того, чтобы эти эффекты стали отчётливо наблюдаемыми, необходимо так изменить параметры исходного сигнала, чтобы сдвиг частоты за время импульса, по крайней мере, начал превышать ширину спектра его огибающей.
Действительно, для импульса гауссовой формы ширина спектра Dnp связана с его длительностью соотношением Dnp tp0 = 2 ln 2/p. Подставляя Dnp в выражение для определения скорости чирпа, получаем |  | = 1, т. е. обусловленные чирпом особенности динамики распространения импульсов станут преобладающими только при выполнении условия |
| = 1, т. е. обусловленные чирпом особенности динамики распространения импульсов станут преобладающими только при выполнении условия |  | > 1. Для иллюстрации этого явления увеличим сдвиг частоты в обсуждаемом примере с 108Гц до 109Гц, оставив все остальные параметры сигнала без изменений. В этом случае |
| > 1. Для иллюстрации этого явления увеличим сдвиг частоты в обсуждаемом примере с 108Гц до 109Гц, оставив все остальные параметры сигнала без изменений. В этом случае |  | » 2.27 и m min = 0.184. Из выражения (5.19) находим t pmin, которая оказывается в 2.5 раза меньше длительности исходного импульса, составляя 0.4 109с. Поскольку величина mminбольше чем в предыдущем случае, то и значение параметра Lmin, при котором будет достигаться максимальное сжатие импульса, возрастает примерно до 3000 км.
| » 2.27 и m min = 0.184. Из выражения (5.19) находим t pmin, которая оказывается в 2.5 раза меньше длительности исходного импульса, составляя 0.4 109с. Поскольку величина mminбольше чем в предыдущем случае, то и значение параметра Lmin, при котором будет достигаться максимальное сжатие импульса, возрастает примерно до 3000 км.
Приведенные расчёты показывают, что получить сколько-нибудь значительное сужение импульсов наносекундной длительности практически невозможно. Однако из этих же расчётов следует, что импульсы такой длительности даже при минимальном чирпе распространяются на тысячи километров без уширения, так как условие L < Lmin соответствует стадии сжатия сигнала.
Переходя в пикосекундную область и сохраняя те же соотношения между параметрами t0 и Dn получаем следующие результаты для импульса длительностью в 1 пикосекунду: t 0» 0.85 10-12 с, Dn» 1011 Гц, tpmin » 0.975 10-12 с, Lmin» 2.7м. На длине волны l = 0.9мкм сдвигу частоты Dn = 1011Гц соответствует Dl = 2.7 ÅПятикратное увеличение скорости «чирпа» до значения Dn = 5 1011Гц, что соответствует |  |» 1.13, приведет к минимальной длительности tpmin = 0.66 10-12 с уже на длине 6.3 м.
|» 1.13, приведет к минимальной длительности tpmin = 0.66 10-12 с уже на длине 6.3 м.
Таким образом, всего лишь несколько метров оптического волокна может оказаться вполне достаточно для того, чтобы существенно уменьшить длительность импульса, если частота оптической несущей меняется достаточно быстро. В области субпикосекундных длительностей (tp0 £ 10-13 с) «длинными» оказываются любые оптические устройства с характерными линейными размерами порядка 1 см.
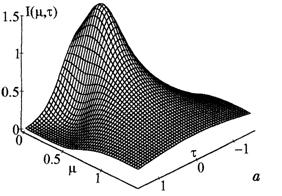
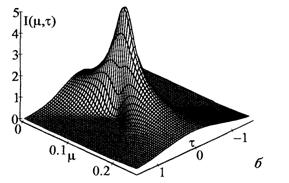
Рис.8.6. Сжатие гауссова импульса с линейным чирпом. Значения безразмерной величины чирпа: а)  = -1, б)
= -1, б)  = -5.
= -5.
Типичная картина деформации формы импульса, рассчитанная на основе (5.15), показана на рис.8.6. Из первого рисунка, соответствующего граничному случаю |  | = 1, можно легко оценить масштабы тех изменений в форме огибающей, которые возникают при равенстве сдвига несущей частоты сигнала за счёт чирпа ширине спектра огибающей этого импульса. На втором рисунке показан случай предельно большого чирпа, приводящий к схлопыванию импульса в некоторой промежуточной точке.
| = 1, можно легко оценить масштабы тех изменений в форме огибающей, которые возникают при равенстве сдвига несущей частоты сигнала за счёт чирпа ширине спектра огибающей этого импульса. На втором рисунке показан случай предельно большого чирпа, приводящий к схлопыванию импульса в некоторой промежуточной точке.
Характерно, что независимо от величины чирпа сжатый импульс возвращается к своему исходному состоянию на расстоянии вдвое большем той величины, при которой происходило его максимальное сжатие.
Модель импульса гауссовой формы позволяет достаточно просто проанализировать многие свойства сигналов с линейным чирпом, распространяющихся в диспергирующей среде. Получающиеся при этом простые соотношения позволяют дать правильную качественную картину деформации огибающей и для импульсов другой формы - близкой к гауссовой, а также определить порядки величин тех параметров, которые представляют практический интерес.




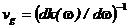 . Считая vg функцией частоты, вычислим приращение этой функции в окрестности точки w 0
. Считая vg функцией частоты, вычислим приращение этой функции в окрестности точки w 0
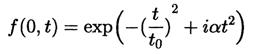




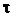 ) в виде отдельного сомножителя
) в виде отдельного сомножителя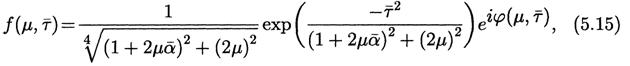
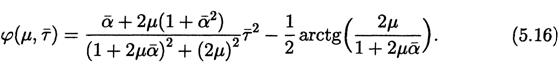



 = 0, 2 -
= 0, 2 - 
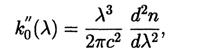

 B 1 = 0.6961663 l12 = 0.004679148 мкм2,
B 1 = 0.6961663 l12 = 0.004679148 мкм2,
 раз по сравнению с исходной. Это обстоятельство следует принимать во внимание при определении коэффициента затухания оптического волокна импульсными методами.
раз по сравнению с исходной. Это обстоятельство следует принимать во внимание при определении коэффициента затухания оптического волокна импульсными методами.