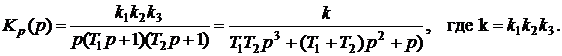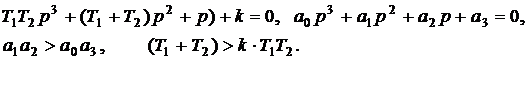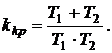Реферат
на тему:
"Устойчивость линейных систем автоматического управления"
Общие понятия устойчивости
Устойчивость – это свойство системы возвращаться в исходное состояние после вывода ее из состояния равновесия и прекращения действия возмущения. Устойчивость – это одно из основных требований, предъявляемых к системе. Если система не устойчива, то она не работоспособна. Рассмотрим математическое понятие устойчивости.
Движение линейной системы автоматического управления описывается линейным, неоднородным уравнением:
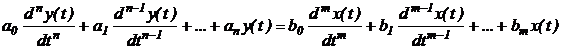
при этом правая часть – входное воздействие, а левая – реакция выхода.
Решение уравнения можно записать в виде:
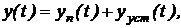 (1)
(1)
где 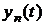 - представляет собой общее решение однородного уравнения и определяет переходный процесс;
- представляет собой общее решение однородного уравнения и определяет переходный процесс; 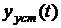 - представляет собой частное решение неоднородного уравнения и определяет установившийся режим.
- представляет собой частное решение неоднородного уравнения и определяет установившийся режим.
Общее решение однородного уравнения имеет вид:
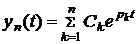 , (2)
, (2)
где: Ск – постоянные интегрирования, которые зависят от начальных условий; 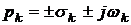 - корни характеристического уравнения:
- корни характеристического уравнения:
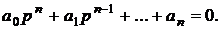
Рассмотрим характер решения при различных значениях корней характеристического уравнения.
1. Если корни действительные однократные
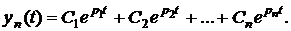
2. Если корни действительные кратные
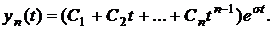
3. Если корни комплексно – сопряженные однократные
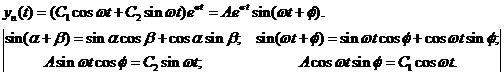
4. Пусть корни комплексно – сопряженные кратные
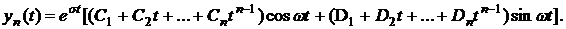
Для того чтобы система была устойчивой решение должно удовлетворять условию
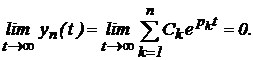 (3)
(3)
Это условие выполняется, если корни характеристического уравнения системы расположены в левой полуплоскости комплексной плоскости P.
Для устойчивости линейной системы необходимо и достаточно, чтобы корни ее характеристического уравнения располагались в левой полуплоскости комплексной плоскости P.
Характеристическое уравнение системы можно представить в виде:
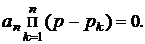 (4)
(4)
Если уравнение содержит хотя бы один положительный корень, то хотя бы один коэффициент характеристического уравнения будет отрицательным. Необходимое, но недостаточное условие устойчивости (при n > 2) системы – это положительность коэффициентов характеристического уравнения.
Для нахождения корней характеристического уравнения необходимо решать алгебраические уравнения. Аналитическое решение уравнений 3-го и 4-го порядка громоздки, а уравнение выше 4-го порядка не имеют аналитического решения.
В теории автоматического управления разработан ряд так называемых критериев устойчивости, которые позволяют, не решая уравнений определять устойчивость систем.
Рис. 3
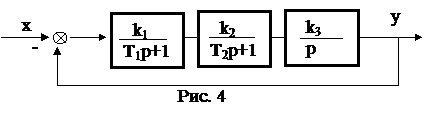
Пример. Для заданной системы (рис. 4) определить условие устойчивости, частоту собственных колебаний системы и критический коэффициент усиления, т.е. коэффициент усиления, при котором система находится на границе устойчивости.
Определить устойчивость при T1 = T2 = 1 c и kv = 1 c-1.
Решение:
1. Определяем передаточную функцию разомкнутой системы
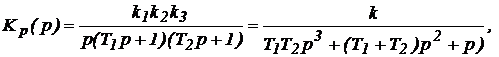
где 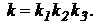
2. Определяем передаточную функцию замкнутой системы
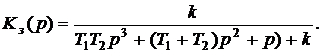
3. Запишем характеристическое уравнение

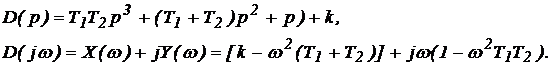
4. Определим частоту собственных колебаний системы и критический коэффициент усиления из условия границы устойчивости
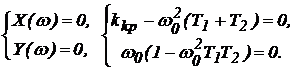
Откуда частота собственных колебаний системы равна:
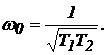
Критический коэффициент усиления равен:
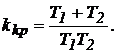
5. Определим устойчивость при T1 = T2 = 1 c и kv = 1 c-1.

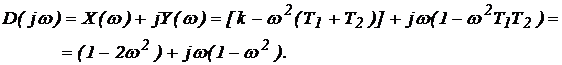
5. Строим характеристическую кривую  (рис. 5) по данным, приведенным в таблице 1.
(рис. 5) по данным, приведенным в таблице 1.
Таблица 1
| w
| 0
| 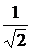
| 1
| ¥
|
| X(w)
| 1
| 0
| -1
| -¥
|
| Y(w)
| 0
| 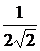
| 0
| -¥
|
В соответствии с критерием Михайлова, рассматриваемая система является устойчивой.
Литература
1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.
2. Брюханов В.Н. и др. Теория автоматического управления. – М: Высшая школа, 2000.
3. Егупов Н.Д., Пупков К.А., Баркин А.И. Синтез регуляторов систем автоматического управления. МГТУ им. Н.Э. Баумана, 2004.
4. Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. ФИЗМАТЛИТ, 2007. – 168 с.
5. Лукас В.А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.
6. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В.А. Бесекерского. – M.: Наука, 1978.
7. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 198 – 712 с.
Реферат
на тему:
"Устойчивость линейных систем автоматического управления"
Общие понятия устойчивости
Устойчивость – это свойство системы возвращаться в исходное состояние после вывода ее из состояния равновесия и прекращения действия возмущения. Устойчивость – это одно из основных требований, предъявляемых к системе. Если система не устойчива, то она не работоспособна. Рассмотрим математическое понятие устойчивости.
Движение линейной системы автоматического управления описывается линейным, неоднородным уравнением:
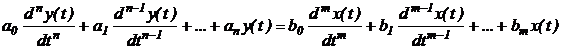
при этом правая часть – входное воздействие, а левая – реакция выхода.
Решение уравнения можно записать в виде:
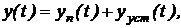 (1)
(1)
где 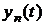 - представляет собой общее решение однородного уравнения и определяет переходный процесс;
- представляет собой общее решение однородного уравнения и определяет переходный процесс; 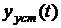 - представляет собой частное решение неоднородного уравнения и определяет установившийся режим.
- представляет собой частное решение неоднородного уравнения и определяет установившийся режим.
Общее решение однородного уравнения имеет вид:
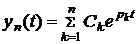 , (2)
, (2)
где: Ск – постоянные интегрирования, которые зависят от начальных условий; 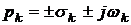 - корни характеристического уравнения:
- корни характеристического уравнения:
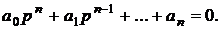
Рассмотрим характер решения при различных значениях корней характеристического уравнения.
1. Если корни действительные однократные
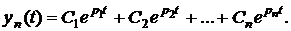
2. Если корни действительные кратные
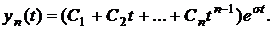
3. Если корни комплексно – сопряженные однократные
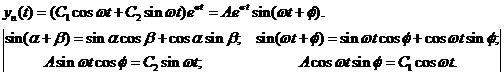
4. Пусть корни комплексно – сопряженные кратные
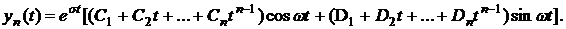
Для того чтобы система была устойчивой решение должно удовлетворять условию
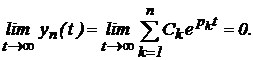 (3)
(3)
Это условие выполняется, если корни характеристического уравнения системы расположены в левой полуплоскости комплексной плоскости P.
Для устойчивости линейной системы необходимо и достаточно, чтобы корни ее характеристического уравнения располагались в левой полуплоскости комплексной плоскости P.
Характеристическое уравнение системы можно представить в виде:
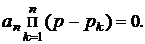 (4)
(4)
Если уравнение содержит хотя бы один положительный корень, то хотя бы один коэффициент характеристического уравнения будет отрицательным. Необходимое, но недостаточное условие устойчивости (при n > 2) системы – это положительность коэффициентов характеристического уравнения.
Для нахождения корней характеристического уравнения необходимо решать алгебраические уравнения. Аналитическое решение уравнений 3-го и 4-го порядка громоздки, а уравнение выше 4-го порядка не имеют аналитического решения.
В теории автоматического управления разработан ряд так называемых критериев устойчивости, которые позволяют, не решая уравнений определять устойчивость систем.
Критерий устойчивости Рауса-Гурвица
Для устойчивости линейной системы необходимо и достаточно, чтобы при а0 >0 определитель Гурвица, составленный для характеристического уравнения 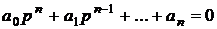 , и все его диагональные миноры были положительны.
, и все его диагональные миноры были положительны.
Определитель Гурвица имеет вид:
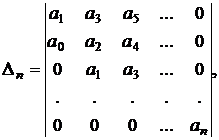 (5)
(5)
Диагональные миноры определяются соотношениями
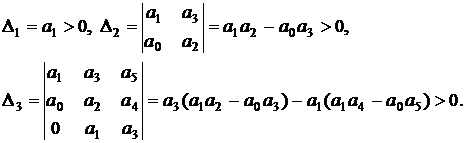 (6)
(6)
Рассмотрим частные случаи
1. Для системы первого порядка (n = 1) характеристическое уравнение имеет вид:
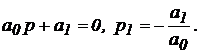 Условие устойчивости:
Условие устойчивости: 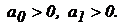
2. Для системы второго порядка (n=2) характеристическое уравнение имеет вид:
3.
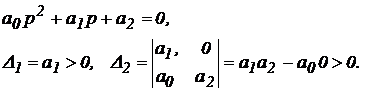
Условие устойчивости: 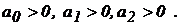
4. Для системы третьего порядка (n = 3) характеристическое уравнение имеет вид:
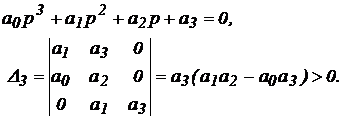
Условие устойчивости: 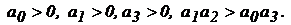
Для систем 1-го и 2-го порядка положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости системы. Для системы 3-го порядка должно выполняться дополнительное условие 
Достоинство критерия:
1. Высокая точность, так как это алгебраический критерий.
2. Простота для систем невысокого порядка.
Недостатки критерия:
1. Необходимо иметь математическое описание системы.
2. Сложность применения для систем высокого порядка.
Рассмотрим примеры определения устойчивости по критерию Гурвица.
Пример 1. Определить устойчивость системы, если ее характеристическое уравнение имеет вид: 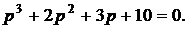
Условие устойчивости 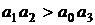 не выполняется, следовательно, система не устойчива.
не выполняется, следовательно, система не устойчива.
Пример 2. Определить устойчивость если передаточная функция разомкнутой системы имеет вид
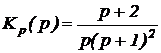 .
.
Решение:
1. Определяем передаточную функцию замкнутой системы
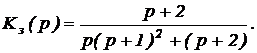
2. Запишем характеристическое уравнение и условие устойчивости
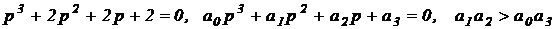 .
.
Условие устойчивости выполняется, следовательно, система устойчива.
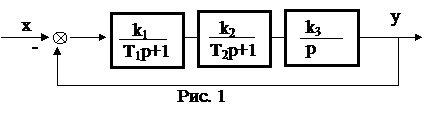
Пример 3. Для заданной системы (рис. 1) определить условие устойчивости и критический коэффициент усиления, т.е. коэффициент усиления, при котором система находится на границе устойчивости.
Решение:
3. Определяем передаточную функцию разомкнутой системы
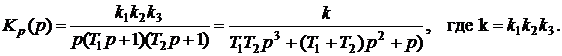
4. Определяем передаточную функцию замкнутой системы
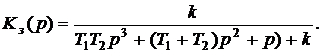
5. Запишем характеристическое уравнение и условие устойчивости
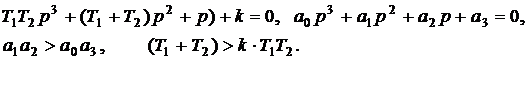
4. Определим критический коэффициент усиления
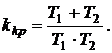



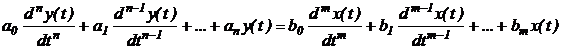
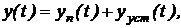 (1)
(1)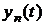 - представляет собой общее решение однородного уравнения и определяет переходный процесс;
- представляет собой общее решение однородного уравнения и определяет переходный процесс; 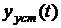 - представляет собой частное решение неоднородного уравнения и определяет установившийся режим.
- представляет собой частное решение неоднородного уравнения и определяет установившийся режим.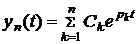 , (2)
, (2)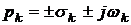 - корни характеристического уравнения:
- корни характеристического уравнения: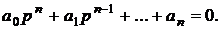
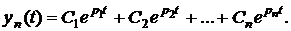
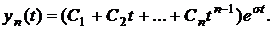
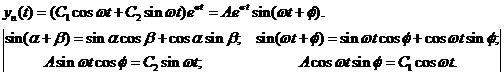
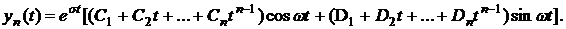
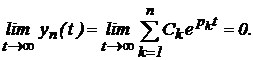 (3)
(3)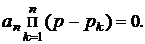 (4)
(4)
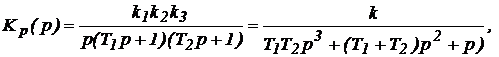
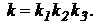
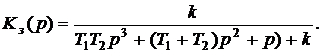

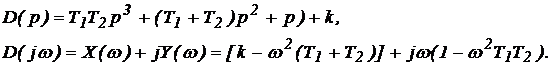
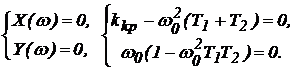
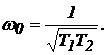
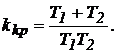
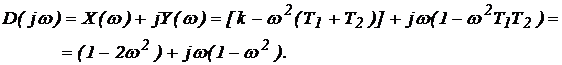
 (рис. 5) по данным, приведенным в таблице 1.
(рис. 5) по данным, приведенным в таблице 1.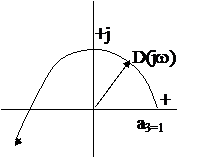
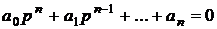 , и все его диагональные миноры были положительны.
, и все его диагональные миноры были положительны.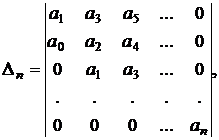 (5)
(5)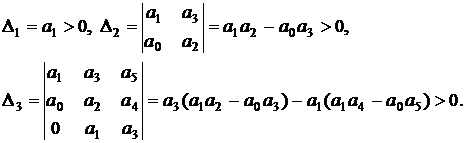 (6)
(6)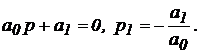 Условие устойчивости:
Условие устойчивости: 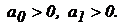
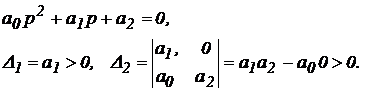
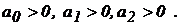
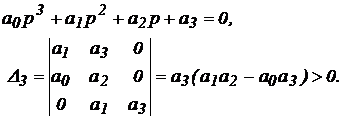
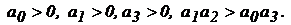

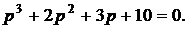
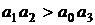 не выполняется, следовательно, система не устойчива.
не выполняется, следовательно, система не устойчива.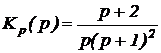 .
.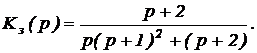
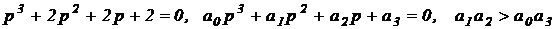 .
.