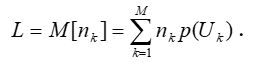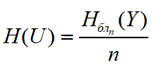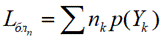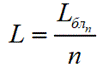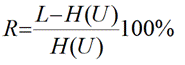Информация по Хартли
● Подходы к измерению количества информации
Существует три подхода к измерению количества информации:
комбинаторный Р. Хартли, вероятностный К. Шеннона и алго-
ритмический А.Н. Колмогоров.
● Основные положения подхода, который применял Хартли
Количество информации есть некоторая функция от числа состояний источника информации.
Комбинаторный подход Хартли —для равновероятных состояний источника информации.
● Свойства функции числа состояний системы
1) Если система имеет только одно состояние, то количество информации в ней равно нулю.
I = I(1) = 0.
2) Если число состояний одной системы больше числа состояний другой системы, то и количество информации в первой системе больше количества информации чем во второй системе.
Есть две системы I1 и I2 с возможными состояниями n1 и n2, то если n2 > n1, то и I(n2) > I(n1).
3) Пусть n1 – число состояний одной системы, а число n2 – число состояний другой системы. Количества информации в них равны соответственно
I1 = I(n1),
I2 = I(n2).
Количество информации в объединенной системе равно:
I(n) = I(n1 · n2).
I(n1·n2) = I(n1) + I(n2).
● Формула Хартли

● Области применения формулы Хартли
Расчет количества информации в системах с равновероятными состояниями. Но если вероятности состояний источников не равны, то формула Хартли не работает.
Энтропия как мера количества информации. Формула Шеннона для вычисления количества информации в дискретных источниках.
● Подходы к измерению количества информации
Существует три подхода к измерению количества информации:
комбинаторный Р. Хартли, вероятностный К. Шеннона и алго-
ритмический А.Н. Колмогоров.
● Преимущества логарифмической меры информации:
•практически более удобна, поскольку такие параметры, как
ширина полосы, число реле имеют тенденцию изменяться линей-
но с логарифмом числа возможных состояний (добавление одно-
го реле удваивает количество возможных состояний);
•близка к интуитивному представлению о подходящей мере,
поскольку каждый чувствует, что в двух карточках в 2 раза больше
информации, чем в одной, а два идентичных канала удваивают
пропускную способность;
•более удобна с математической точки зрения, поскольку
многие предельные переходы весьма просты при применении
логарифмов.
● Суть вероятностного подхода
Клод Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.
В основу вероятностной теории информации К. Шеннон
положил метод исчислений количества новой (непредсказуемой)
и избыточной (предсказуемой) информации, содержащейся в
сообщениях, передаваемых по каналам технической связи.
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Формула Шеннона для вычисления количества информации в дискретных источниках
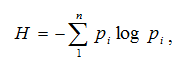
Аксиомы теории информации.
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Аксиомы теории информации
Шеннон ввел три аксиомы, в которых рассматриваются уже не
только состояния, но и вероятности состояний источника информации.
Аксиома 1.
Мера неопределенности есть непрерывная функция
вероятностей состояний физической системы.
Аксиома 2.
Если состояния источника равновероятны, то мера
неопределенности есть монотонно возрастающая функция от числа
состояний источника.
Аксиома 3.
Если неопределенность источника информации
раскрывается по этапам, то полная неопределенность равна взве-
шенной сумме неопределенностей, полученных на каждом этапе,
т. е. сохраняется произвольность выбора.
● Формула Шеннона для вычисления количества информации в дискретных источниках
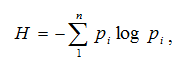
Свойства энтропии
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Св-во 1 (нулевая энтропия)
Неопределенность (энтропия) физической системы равна нулю:
H = H(p1, p2, …, pn) = 0,
в том случае, если одно из чисел p1, p2, …, pn равно 1, а остальные равны нулю.
● Св-во 2 (максимальная энтропия)
Энтропия H(p1, p2, …, pn) максимальна, когда все состояния источника равновероятны.
● Св-во 3 (увеличение энтропии)
Всякое изменение вероятностей в сторону их выравнивания увеличивает энтропию H(p1, p2, …, pn).
● Св-во 4 (вычисление энтропии)
Энтропия есть математическое ожидание функции (-logp i).
Единицы энтропии
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Понятие единицы измерения энтропии
За единицу измерения энтропии может быть принята энтропия любого объекта, специально заданного так, чтобы:

Количество информации, которое может быть получено в этом простейшем случае (2 равновероятными событиями), принято за единицу количества информации - бит.
● Понятие бита. Перевод в биты
бит – это сообщение о том, что система с 2 равновероятными состояниями приняла одно из этих состояний вычисленная с помощью логарифма с основанием 2.
1 бит = 1/1,44 нат = 1/3,32 дит
● Понятие ната. Перевод в наты
нат – энтропия системы с “е” равновероятными состояниями, вычисленная с помощью логарифма с основанием “е”.
1 бит = 1/1,44 нат = 1/3,32 дит
● Понятие дита. Перевод в диты
дит (di t – di gital uni t) – энтропия системы с десятью равновероятными состояниями, вычисленная с помощью логарифма с основанием десять.
1 бит = 1/1,44 нат = 1/3,32 дит
Энтропия сложных систем
● Объединение систем
Объединением двух систем X и Y с возможными состояниями x1, x2, … xn и y1, y2, … ym будем понимать сложную систему XY, состояния которой (xi yi) представляют собой всевозможные попарные комбинации состояний xiyj систем X и Y.
● Энтропия объединения взаимно независимых источников информации
Энтропия объединения независимых источников равна сумме энтропий.

● Энтропия объединения взаимно зависимых источников информации
Если две взаимно зависимые системы объединяются в одну, то энтропия объединенной системы равна энтропии одной из ее составных частей плюс средняя условная энтропия второй части относительно первой.
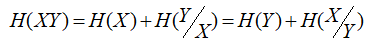
● Понятие функции распределения
Функция распределения F(x) есть неубывающая функция аргумента x:  В пределе при
В пределе при 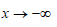 функция распределения равна нулю: F(x) = 0. В пределе при
функция распределения равна нулю: F(x) = 0. В пределе при 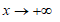 функция распределения равна единице: F(x) = 1.
функция распределения равна единице: F(x) = 1.
Можно сказать проще, функция распределения – это вероятность того, что некоторое случайное число лежит левее аргумента, как это показано на рисунке 3.3.
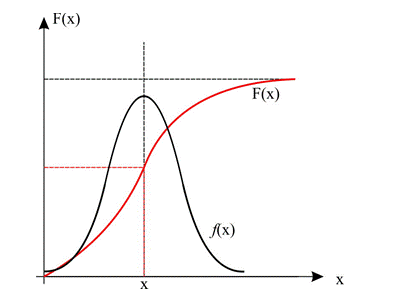
Рисунок 3.3 – Функция распределения
● Понятие дифференциальной энтропии
Приведенная, относительная или дифференциальная энтропия:
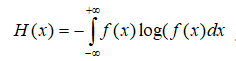
Теорема Шеннона.
При кодировании множества состояний дискретного источника с энтропией H(U) в алфавите из m букв средняя длина кодового слова не может быть меньше, чем  Если вероятность состояний источника представляет собой целочисленные степени числа букв m (при m = 2, то есть, 2-2, 2-2, 2-3 2-4, и т.д.), то длина кодового слова равна нижней границе.
Если вероятность состояний источника представляет собой целочисленные степени числа букв m (при m = 2, то есть, 2-2, 2-2, 2-3 2-4, и т.д.), то длина кодового слова равна нижней границе.
Если вероятности состояний источника не являются целочисленными степенями числа m, то точное достижение указанной нижней границы в общем случае оказывается невозможным. Однако, при кодировании достаточно длинных последовательностей – блоков, можно приблизить длину кодового слова, приходящегося в среднем на одно состояние, к нижней границе с любой, наперед заданной точностью.
● Алгоритм оптимального кодирования Шеннона – Фано
1. Множество состояний разбивается на две группы, причем, суммарные вероятности групп должны быть равны.
2. Если кодируемое состояние относится к первой группе, то в качестве первой буквы кодового слова берем 0, а для второй группы – 1.
3. Затем каждая группа разбивается на 2 равные по суммарной вероятности подгруппы и символ 0 берется для первой подгруппы, а символ 1 – для второй подгруппы.
4. Разбиения проводятся до тех пор, пока в подгруппе не останется единственное из кодируемых состояний.
● Расчет минимальной средней длины кодового слова
Минимальная средняя длина кодового слова равна:

● Расчет средней длины кодового слова
Средняя длина кодового слова равна математическому ожиданию индивидуальных длин кодовых слов:
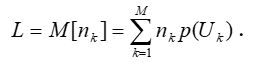
● Расчет избыточности
Избыточность (показывает, на сколько средняя длина кодового слова превышает теоретический минимум) определяется по формуле:

Блочное кодирование.
● Теорема Шеннона о существовании оптимальных кодов(см. 8)
При кодировании множества состояний дискретного источника с энтропией H(U) в алфавите из m букв средняя длина кодового слова не может быть меньше, чем  .
.
Если вероятность состояний источника представляет собой целочисленные степени числа букв m (при m = 2, то есть, 2-2, 2-2, 2-3 2-4, и т.д.), то длина кодового слова равна нижней границе.
Если вероятности состояний источника не являются целочисленными степенями числа m, то точное достижение указанной нижней границы в общем случае оказывается невозможным. Однако, при кодировании достаточно длинных последовательностей – блоков, можно приблизить длину кодового слова, приходящегося в среднем на одно состояние, к нижней границе с любой, наперед заданной точностью.
● Алгоритм кодирования блоками
При кодировании блоками сообщение передается блоками по n сообщений. Число кодовых слов будет равно числу комбинаций из 2-х по n (2 в степени n). Расписываются все возможные блоки и их вероятность рассчитывается как перемножение вероятностей каждого сообщения в блоке. Далее алгоритм аналогичен описанному в п. 9 для кодирования отдельных сообщений.
● Энтропия ансамбля блоков и энтропия, приходящаяся на букву
Энтропия ансамбля блоков (n - число сообщений в блоке):

Тогда энтропия, приходящаяся на одну букву:
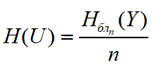
● Средняя длина кодового слова и часть кодового слова, приходящаяся на букву
Средняя длина кодового слова для блока из n сообщений:
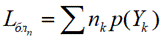
Длина части кодового слова, приходящаяся на одно состояние источника:
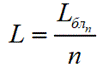
● Расчет избыточности
Избыточность рассчитывается по формуле:
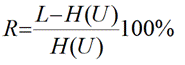
Информация по Хартли
● Подходы к измерению количества информации
Существует три подхода к измерению количества информации:
комбинаторный Р. Хартли, вероятностный К. Шеннона и алго-
ритмический А.Н. Колмогоров.
● Основные положения подхода, который применял Хартли
Количество информации есть некоторая функция от числа состояний источника информации.
Комбинаторный подход Хартли —для равновероятных состояний источника информации.
● Свойства функции числа состояний системы
1) Если система имеет только одно состояние, то количество информации в ней равно нулю.
I = I(1) = 0.
2) Если число состояний одной системы больше числа состояний другой системы, то и количество информации в первой системе больше количества информации чем во второй системе.
Есть две системы I1 и I2 с возможными состояниями n1 и n2, то если n2 > n1, то и I(n2) > I(n1).
3) Пусть n1 – число состояний одной системы, а число n2 – число состояний другой системы. Количества информации в них равны соответственно
I1 = I(n1),
I2 = I(n2).
Количество информации в объединенной системе равно:
I(n) = I(n1 · n2).
I(n1·n2) = I(n1) + I(n2).
● Формула Хартли

● Области применения формулы Хартли
Расчет количества информации в системах с равновероятными состояниями. Но если вероятности состояний источников не равны, то формула Хартли не работает.
Энтропия как мера количества информации. Формула Шеннона для вычисления количества информации в дискретных источниках.
● Подходы к измерению количества информации
Существует три подхода к измерению количества информации:
комбинаторный Р. Хартли, вероятностный К. Шеннона и алго-
ритмический А.Н. Колмогоров.
● Преимущества логарифмической меры информации:
•практически более удобна, поскольку такие параметры, как
ширина полосы, число реле имеют тенденцию изменяться линей-
но с логарифмом числа возможных состояний (добавление одно-
го реле удваивает количество возможных состояний);
•близка к интуитивному представлению о подходящей мере,
поскольку каждый чувствует, что в двух карточках в 2 раза больше
информации, чем в одной, а два идентичных канала удваивают
пропускную способность;
•более удобна с математической точки зрения, поскольку
многие предельные переходы весьма просты при применении
логарифмов.
● Суть вероятностного подхода
Клод Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.
В основу вероятностной теории информации К. Шеннон
положил метод исчислений количества новой (непредсказуемой)
и избыточной (предсказуемой) информации, содержащейся в
сообщениях, передаваемых по каналам технической связи.
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Формула Шеннона для вычисления количества информации в дискретных источниках
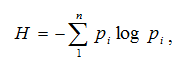
Аксиомы теории информации.
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Аксиомы теории информации
Шеннон ввел три аксиомы, в которых рассматриваются уже не
только состояния, но и вероятности состояний источника информации.
Аксиома 1.
Мера неопределенности есть непрерывная функция
вероятностей состояний физической системы.
Аксиома 2.
Если состояния источника равновероятны, то мера
неопределенности есть монотонно возрастающая функция от числа
состояний источника.
Аксиома 3.
Если неопределенность источника информации
раскрывается по этапам, то полная неопределенность равна взве-
шенной сумме неопределенностей, полученных на каждом этапе,
т. е. сохраняется произвольность выбора.
● Формула Шеннона для вычисления количества информации в дискретных источниках
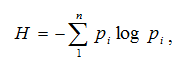
Свойства энтропии
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Св-во 1 (нулевая энтропия)
Неопределенность (энтропия) физической системы равна нулю:
H = H(p1, p2, …, pn) = 0,
в том случае, если одно из чисел p1, p2, …, pn равно 1, а остальные равны нулю.
● Св-во 2 (максимальная энтропия)
Энтропия H(p1, p2, …, pn) максимальна, когда все состояния источника равновероятны.
● Св-во 3 (увеличение энтропии)
Всякое изменение вероятностей в сторону их выравнивания увеличивает энтропию H(p1, p2, …, pn).
● Св-во 4 (вычисление энтропии)
Энтропия есть математическое ожидание функции (-logp i).
Единицы энтропии
● Понятие энтропии
Энтропия – это среднее количество информации, приходящееся на одно состояние физической системы.
● Понятие единицы измерения энтропии
За единицу измерения энтропии может быть принята энтропия любого объекта, специально заданного так, чтобы:

Количество информации, которое может быть получено в этом простейшем случае (2 равновероятными событиями), принято за единицу количества информации - бит.
● Понятие бита. Перевод в биты
бит – это сообщение о том, что система с 2 равновероятными состояниями приняла одно из этих состояний вычисленная с помощью логарифма с основанием 2.
1 бит = 1/1,44 нат = 1/3,32 дит
● Понятие ната. Перевод в наты
нат – энтропия системы с “е” равновероятными состояниями, вычисленная с помощью логарифма с основанием “е”.
1 бит = 1/1,44 нат = 1/3,32 дит
● Понятие дита. Перевод в диты
дит (di t – di gital uni t) – энтропия системы с десятью равновероятными состояниями, вычисленная с помощью логарифма с основанием десять.
1 бит = 1/1,44 нат = 1/3,32 дит
Энтропия сложных систем
● Объединение систем
Объединением двух систем X и Y с возможными состояниями x1, x2, … xn и y1, y2, … ym будем понимать сложную систему XY, состояния которой (xi yi) представляют собой всевозможные попарные комбинации состояний xiyj систем X и Y.
● Энтропия объединения взаимно независимых источников информации
Энтропия объединения независимых источников равна сумме энтропий.

● Энтропия объединения взаимно зависимых источников информации
Если две взаимно зависимые системы объединяются в одну, то энтропия объединенной системы равна энтропии одной из ее составных частей плюс средняя условная энтропия второй части относительно первой.
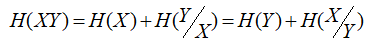
● Понятие функции распределения
Функция распределения F(x) есть неубывающая функция аргумента x:  В пределе при
В пределе при 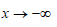 функция распределения равна нулю: F(x) = 0. В пределе при
функция распределения равна нулю: F(x) = 0. В пределе при 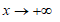 функция распределения равна единице: F(x) = 1.
функция распределения равна единице: F(x) = 1.
Можно сказать проще, функция распределения – это вероятность того, что некоторое случайное число лежит левее аргумента, как это показано на рисунке 3.3.

Рисунок 3.3 – Функция распределения
● Понятие дифференциальной энтропии
Приведенная, относительная или дифференциальная энтропия:
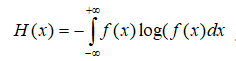




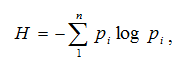


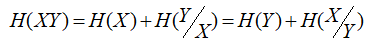
 В пределе при
В пределе при 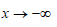 функция распределения равна нулю: F(x) = 0. В пределе при
функция распределения равна нулю: F(x) = 0. В пределе при 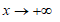 функция распределения равна единице: F(x) = 1.
функция распределения равна единице: F(x) = 1.
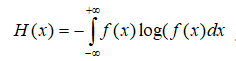
 Если вероятность состояний источника представляет собой целочисленные степени числа букв m (при m = 2, то есть, 2-2, 2-2, 2-3 2-4, и т.д.), то длина кодового слова равна нижней границе.
Если вероятность состояний источника представляет собой целочисленные степени числа букв m (при m = 2, то есть, 2-2, 2-2, 2-3 2-4, и т.д.), то длина кодового слова равна нижней границе.