Критерий Гурвица
Критерий записывается в виде определителей, составленных из коэффициентов характеристического уравнения системы

Характеристическое уравнение представляет собой знаменатель передаточной функции, приравненный к нулю. Для характеристического уравнения составим квадратную матрицу коэффициентов, содержащую n строк и n столбцов по следующим правилам:
1) по диагонали выписываются все коэффициенты, начиная с а n-1 в порядке убывания индексов до a0;
2) все горизонтальные строки правее диагонали заполняются коэффициентами с возрастающими индексами, а левее - с убывающими индексами;
3) оставшиеся места (индексы коэффициентов больше n или меньше нуля) заполняются нулями, т.е.
 .
.
Критерий устойчивости Гурвица сводится к тому, что при а n>0 должны быть больше нуля все n определителей Гурвица (D1, D2,…, D n), получаемых из квадратной матрицы коэффициентов.
Определители Гурвица составляются из главного определителя D n путем отчеркивания соответствующего количества строк и столбцов:
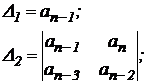
…
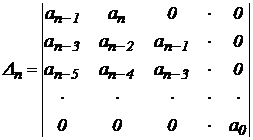 .
.
Последний определитель (главный определитель Гурвица) включает в себя всю матрицу. Но так как в последней строке матрицы все элементы, кроме последнего, равны нулю, то главный определитель Гурвица, выражается через предпоследний следующим образом:
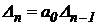 .
.
Однако в устойчивой системе предпоследний определитель тоже должен быть положительным. Поэтому условие положительности последнего определителя сводится к условию а0>0, т.е. к положительности свободного члена характеристического уравнения.
Условия нахождения системы на границе устойчивости можно получить, приравнивая нулю последний определить: D n=0, при положительности всех остальных определителей. Как следует из (4.8), это условие распадается на два условия: а0=0 и D n-1=0. Первое условие соответствует границе устойчивости первого типа (апериодическая граница устойчивости, т.е. наличие нулевого корня) и второе – границе устойчивости второго типа (колебательная граница устойчивости, т.е. наличие пары чисто мнимых корней).
Составим определители Гурвица электромеханической следящей системы:
; ; .
Подставим значения коэффициентов (см. передаточную функцию замкнутой системы), получим определители Гурвица
= 4; = 0,08; = 0,105.
Вывод: так как все определители Гурвица больше 0, то системы устойчива.
Найдем условие нахождения системы на границе устойчивости. Из условия D2 = 0, получаем
a1 a2 – a0 a3 = 0,
1 (T1 + T2) – k T1 T2 = 0.
Из этого условия можно найти области устойчивости для одного из параметров системы. Найдем область устойчивости для коэффициента k.
= 210.
Системы будет устойчивой, если коэффициент передачи системы меньше 210.
Критерий Михайлова
Рассмотрим отдельно левую часть характеристического уравнения, которая представляет собой характеристический полином:
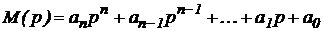 .
.
Подставим в этот полином чисто мнимое значение 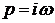 , где w представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического уравнения. При этом получим характеристический комплекс
, где w представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического уравнения. При этом получим характеристический комплекс
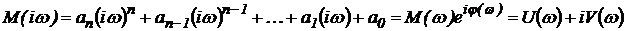 ,
,
где вещественная часть будет содержать четные степени w:
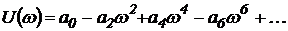 ,
,
а мнимая – нечетные степени w:
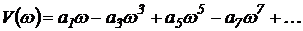 .
.
При фиксированном значении частоты M(i w) - вектор на комплексной плоскости, а функции M(w) и j(w) представляют собой модуль и фазу (аргумент) характеристического комплекса.
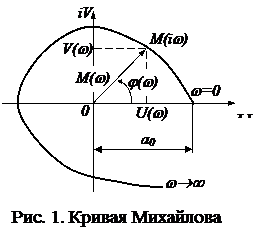 Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы или аргумента j(w) при изменении w от 0 до ¥ равно
Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы или аргумента j(w) при изменении w от 0 до ¥ равно  , где n – степень полинома М(р). Следовательно, система регулирования будет устойчивой. Если полное приращение аргумента j(w) окажется меньше
, где n – степень полинома М(р). Следовательно, система регулирования будет устойчивой. Если полное приращение аргумента j(w) окажется меньше  , то система неустойчива.
, то система неустойчива.
Если все коэффициенты полинома М(р) заданы и задано определенное значение частоты w, то величина M(i w) изобразится на комплексной плоскости в виде точки с координатами U и V или в виде вектора, соединяющего эту точку с началом координат. Если же значение частоты w менять непрерывно от нуля до бесконечности, то вектор будет изменяться по величине и по направлению, описывая своим концом некоторую кривую (годограф), которая называется кривой Михайлова (рис. 9). Практически кривая Михайлова строится по точкам, причем задаются различные значения частоты w и вычисляются U(w) и V(w). Результаты расчетов сводятся в таблицу, по которой затем строится кривая.
Связь между видом кривой Михайлова и знаками вещественных корней характеристического уравнения можно выразить следующим выражением:
 ,
,
где j - результирующий угол поворота вектора M(i w) при изменении w от 0 до ¥, равный сумме углов поворота отдельных сомножителей:
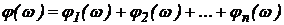
или если записать по приращению аргумента вектора M(i w)
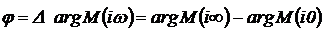
при 
где n – степень характеристического уравнения системы; l – количество корней с положительной вещественной частью, т.е. количество корней лежащих в правой полуплоскости.
А. В. Михайловым был сформулирован следующий критерий устойчивости для линейных систем любого порядка.
Для устойчивости линейной САУ n -го порядка необходимо и достаточно, чтобы вектор M(i w), описывающий кривую Михайлова, при изменении частоты от 0 до ¥ имел угол поворота
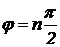 .
.
Для устойчивости системы необходимо, чтобы все корни лежали в левой полуплоскости, т.е. должно быть l=0. Отсюда определяется требуемый результирующий угол поворота вектора.
Итак, для устойчивой системы кривая Михайлова всегда имеет плавную спиралевидную форму и проходит последовательно  квадрантов, начинаясь при
квадрантов, начинаясь при  в точке
в точке 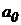 на вещественной оси и уходя в бесконечность при
на вещественной оси и уходя в бесконечность при 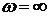 в
в  -м квадранте. На рис. 9 показана кривая Михайлова для устойчивой системы 4 -го порядка.
-м квадранте. На рис. 9 показана кривая Михайлова для устойчивой системы 4 -го порядка.
 Число квадрантов, большее чем n, кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора M(i w) оказывается меньшим чем
Число квадрантов, большее чем n, кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора M(i w) оказывается меньшим чем  (рис. 9).
(рис. 9).
Сказанное выше позволяет сформулировать критерий Михайлова в несколько измененном виде. Для устойчивой системы кривая Михайлова проходит последовательно n квадрантов. Поэтому корни уравнений U(w)=0 и V(w)=0 должны чередоваться. Так как кривая Михайлова всегда начинается с точки, расположенной на оси вещественных (рис. 10), где мнимая часть обращается в нуль: V(w1)= V(0)=0, то при постепенном увеличении частоты от нуля до бесконечности должна обратиться в нуль сначала вещественная часть: U(w2)=0, затем мнимая: V(w3)=0, затем опять вещественная: U(w4)=0 и т.д., причем 0= w1< w2 < w3<…< w n.
Характеристический вектор электромеханической следящей системы получим, подставив p = j w в характеристический полином (знаменатель передаточной функции замкнутой системы)
M(j w) = a0 – a2 w 2 + j (a1 w – a3 w 3).
Система третьего порядка.
Изменяя частоту в диапазоне w = 0…60 с–1 построим кривую Михайлова (рис. 11).
Вывод: т.к. характеристический вектор описывает угол 3 p/2, т.е. последовательно проходит первый, второй и третий квадранты (уходит в бесконечность в третьем квадранте) и порядок системы равен трем, то система устойчива.
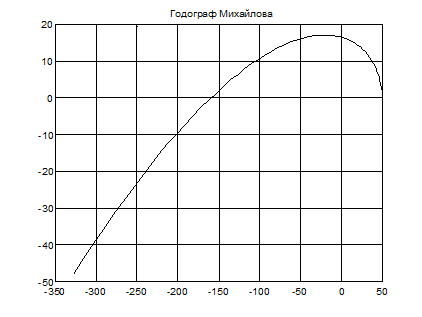
Рис. 11. Кривая Михайлова.
Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы.
Ранее было введено понятие передаточной функции разомкнутой системы. Эта функция может быть представлена в виде
 .
.
Причем степень числителя не может быть выше степени знаменателя, m £ n. При подстановке р= j w получается частотная передаточная функция разомкнутой системы
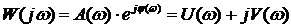 .
.
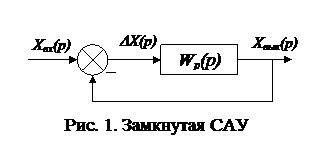 Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных ранее частотных характеристик смысл ее можно объяснить следующим образом. Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией Wр(р) (рис. 12). Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний
Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных ранее частотных характеристик смысл ее можно объяснить следующим образом. Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией Wр(р) (рис. 12). Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний  с амплитудой Авх и частотой w, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону
с амплитудой Авх и частотой w, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону 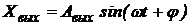 с амплитудой Авых, той же частотой w и фазовым сдвигом j. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
с амплитудой Авых, той же частотой w и фазовым сдвигом j. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
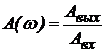 ,
,
а аргумент – сдвиг фаз j.
 Если изменять частоту входного воздействия от - ¥ до + ¥ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 13). Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси. На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например w1, w2, w3 и т.д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты w (рис. 13).
Если изменять частоту входного воздействия от - ¥ до + ¥ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 13). Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси. На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например w1, w2, w3 и т.д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты w (рис. 13).
В реальных системах всегда удовлетворяется условие m< n. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к нулю и точка с частотой w = ± ¥ попадает в начало координат.
Сформулируем достаточные и необходимые требования к амплитудно-фазовой характеристике разомкнутой системы, при выполнении которых система автоматического регулирования в замкнутом состоянии будет устойчивой.
Ограничим вначале задачу и будем рассматривать только такие передаточные функции, которые соответствуют статическим системам. Это значит, что знаменатель не будет иметь в качестве множителя оператор р.
Формулировка критерия для случая устойчивой в замкнутом состоянии системы. Замкнутая система будет устойчивой, если годограф вектора W(j w) или АФЧХ разомкнутой системы при изменении частоты w от 0 до ¥ не охватывает точку с координатами (-1; 0). Это является необходимым и достаточным условием того, чтобы система была устойчивой в замкнутом состоянии (рис. 16).
При определении устойчивости достаточно построить амплитудно-фазовую характеристику только для положительных частот, так как ее ветвь, соответствующая отрицательным частотам, может быть легко получена зеркальным отображением относительно оси вещественных.
На рис. 17 изображен случай так называемой абсолютно устойчивой системы. Этот термин означает, что система остается устойчивой при любом уменьшении коэффициента усиления разомкнутой цепи. Если передаточную функцию разомкнутой статической системы представить в виде:
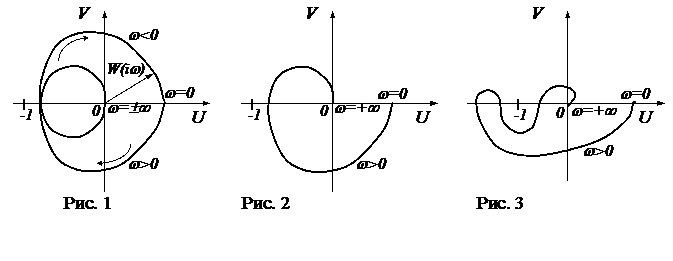
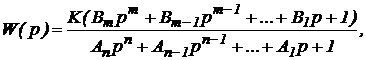
где  ,
,
то нетрудно видеть, что уменьшение общего коэффициента усиления K приводит к уменьшению модуля W(j w), а это в случае, изображенном на рис. 17, не может привести к охвату годографом точки (-1; 0).
На рис. 18 изображен случай так называемой условно устойчивой системы. Здесь система будет устойчивой при значении общего коэффициента усиления, лежащем в некоторых пределах. Как увеличение, так и уменьшение общего коэффициента усиления K может привести к охвату годографом точки, что будет соответствовать неустойчивости системы в замкнутом состоянии.
На рис. 14 изображен случай, когда система находится на границе устойчивости. Граница устойчивости будет колебательного типа. Это вытекает из того, что при некоторой частоте, при которой годограф пересекает точку, имеет место равенство  , что может быть записано в виде
, что может быть записано в виде 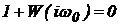 . Это выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р= j w0. Таким образом, чисто мнимый корень является решением характеристического уравнения.
. Это выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р= j w0. Таким образом, чисто мнимый корень является решением характеристического уравнения.
На рис. 15 изображен случай неустойчивой системы.
Обратимся теперь к передаточной функции разомкнутой системы, соответствующей астатизму первого (r=1) или более высоких порядков (r= k). В этом случае передаточная функция может быть представлена в виде
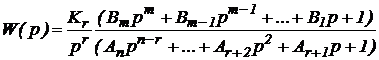 .
.
Будем предполагать, что все корни знаменателя передаточной функции (кроме нулевого корня р=0) лежат в левой полуплоскости, т.е. в разомкнутом состоянии система является нейтрально устойчивой. Амплитудно-фазовая характеристика разомкнутой системы будет иметь разрыв непрерывности в точке w=0. В этой точке модуль А(0) ® ¥, а фаза делает скачок на r ´1800 (r ´ p), т.е. АФЧХ на комплексной плоскости делает поворот по часовой стрелке.
На рис. 19 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы с астатизмом первого порядка. Характеристика начинается в начале координат при
w ®- ¥ и затем уходит в бесконечность при
w ®0 (верхняя ветвь). Далее характеристика дополняется полуокружностью бесконечно большого радиуса так, чтобы вектор
W(i w) повернулся по часовой стрелке на угол равный
p. Нижняя ветвь характеристики соответствует изменению частоты от
0 до
+ ¥. Нетрудно видеть, что характеристика не охватывает точку (
-1; 0), и система в замкнутом состоянии будет устойчивой.
На рис. 20 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы при наличии астатизма второго порядка. Так же как и ранее, здесь можно получить условную устойчивость (рис. 20), колебательную границу устойчивости, если характеристика пройдет через точку (-1; 0), и неустойчивость, если характеристика будет охватывать точку (-1; 0).
Обобщая проведенные рассуждения, получаем, что для определения устойчивости системы с астатизмом любого порядка достаточно построить только одну ветвь амплитудно-фазовой характеристики, соответствующую положительным частотам, которая должна быть дополнена окружностью бесконечно большого радиуса. При этом для устойчивой в замкнутом состоянии системы эта ветвь вместе с частью окружности, заключенной между положительной полуосью вещественных и амплитудно-фазовой характеристикой, соответствующей положительным частотам, не должна охватывать точку (-1; 0) в соответствии с рис. 21.
 Из рис. 21 следует, что абсолютная устойчивость может быть получена при степени астатизма r £2. При большей степени астатизма может быть получена только условная устойчивость.
Из рис. 21 следует, что абсолютная устойчивость может быть получена при степени астатизма r £2. При большей степени астатизма может быть получена только условная устойчивость.
Большое практическое преимущество критерия Найквиста заключается также в том, что он может применяться при использовании логарифмических частотных характеристик, которые во многих случаях могут строиться почти без вычислительной работы. Этот вопрос будет рассмотрен далее.
Исследуем на устойчивость электромеханическую следящую систему. Откладывая значение комплексной передаточной функции разомкнутой системы Wp(j w) на комплексной плоскости при изменении частоты w = 40…500 с–1, получим амплитудно-фазовую характеристику (АФХ) разомкнутой системы.
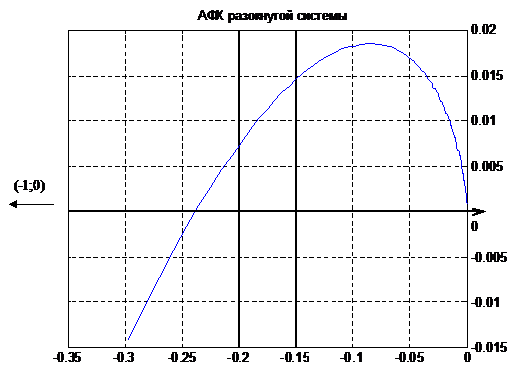
Рис. 22. АФХ разомкнутой системы
Вывод: система устойчива, т.к. кривая Найквиста не охватывает точку с координатами (–1;0).




 .
.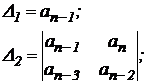
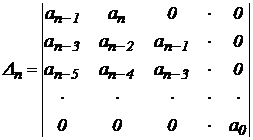 .
.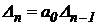 .
.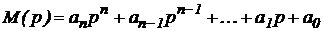 .
.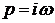 , где w представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического уравнения. При этом получим характеристический комплекс
, где w представляет собой угловую частоту колебаний, соответствующих чисто мнимому корню характеристического уравнения. При этом получим характеристический комплекс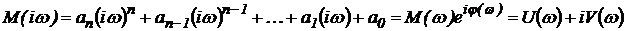 ,
,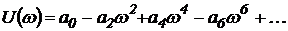 ,
,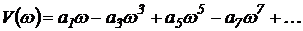 .
. Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы или аргумента j(w) при изменении w от 0 до ¥ равно
Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы или аргумента j(w) при изменении w от 0 до ¥ равно  , где n – степень полинома М(р). Следовательно, система регулирования будет устойчивой. Если полное приращение аргумента j(w) окажется меньше
, где n – степень полинома М(р). Следовательно, система регулирования будет устойчивой. Если полное приращение аргумента j(w) окажется меньше  ,
,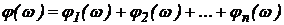
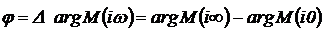
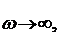
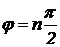 .
. квадрантов, начинаясь при
квадрантов, начинаясь при  в точке
в точке 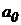 на вещественной оси и уходя в бесконечность при
на вещественной оси и уходя в бесконечность при 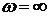 в
в  Число квадрантов, большее чем n, кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора M(i w) оказывается меньшим чем
Число квадрантов, большее чем n, кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота вектора M(i w) оказывается меньшим чем  (рис. 9).
(рис. 9).
 .
.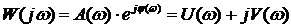 .
.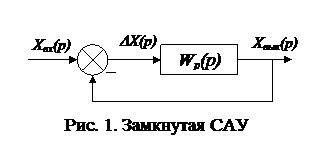 Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных ранее частотных характеристик смысл ее можно объяснить следующим образом. Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией Wр(р) (рис. 12). Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний
Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных ранее частотных характеристик смысл ее можно объяснить следующим образом. Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией Wр(р) (рис. 12). Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний  с амплитудой Авх и частотой w, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону
с амплитудой Авх и частотой w, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону 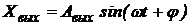 с амплитудой Авых, той же частотой w и фазовым сдвигом j. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
с амплитудой Авых, той же частотой w и фазовым сдвигом j. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин: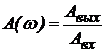 ,
, Если изменять частоту входного воздействия от - ¥ до + ¥ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 13). Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси. На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например w1, w2, w3 и т.д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты w (рис. 13).
Если изменять частоту входного воздействия от - ¥ до + ¥ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 13). Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси. На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например w1, w2, w3 и т.д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты w (рис. 13).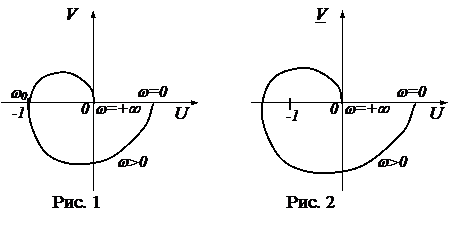
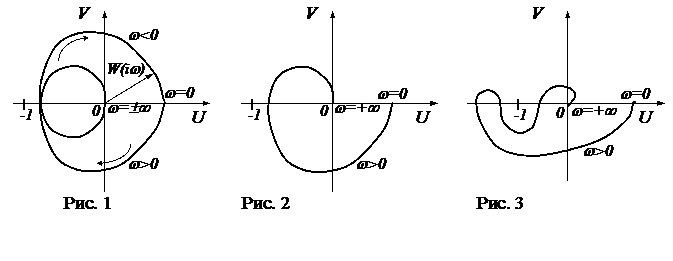
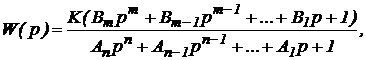
 ,
, , что может быть записано в виде
, что может быть записано в виде 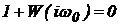 . Это выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р= j w0. Таким образом, чисто мнимый корень является решением характеристического уравнения.
. Это выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р= j w0. Таким образом, чисто мнимый корень является решением характеристического уравнения.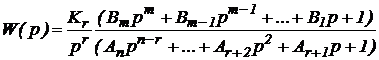 .
.
 Из рис. 21 следует, что абсолютная устойчивость может быть получена при степени астатизма r £2. При большей степени астатизма может быть получена только условная устойчивость.
Из рис. 21 следует, что абсолютная устойчивость может быть получена при степени астатизма r £2. При большей степени астатизма может быть получена только условная устойчивость.



