Число сочетаний из n элементов по k элементов

Факториалы

Для произвольного натурального числа n формулаn!=1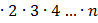

определяет факториал числа n (n! читается, как n – факториал).

Например, 5!=1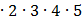

Считается, что0! = 1, 1! = 1.

Перестановки

Рассмотрим следующую задачу.

Задача. 6 карточек пронумерованы числами 1, 2, 3, 4, 5, 6. Карточки наугад выкладываем в ряд. Сколько при этом можно получить различных шестизначных чисел?

Решение. Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое, пятое, шестое. На первое место можно положить одну из 6 карточек. Для этого есть 6 способов. В каждом из этих 6 способов на второе место можно положить одну из оставшихся 5 карточек. Таким образом, существует6·5=30способов, чтобы положить карточки на первое и второе места. В каждом из этих 30 способов на третье место можно положить одну из оставшихся 4 карточек. Следовательно, существует 6·5·4=120 способов, чтобы положить карточки на первое, второе и третье места. В каждом из этих 120 способов на четвертое место можно положить одну из оставшихся 3 карточек. Отсюда вытекает, что существует 6·5·4·3=360 способов, чтобы положить карточки на первое, второе, третье и четвертое места. В каждом из этих 360 способов на пятое место можно положить одну из оставшихся 2 карточек. Следовательно, существует 6·5·4·3·2=720 способов, чтобы положить карточки на первое, второе, третье, четвертое и пятое места. После этого у нас остается одна единственная карточка, которую мы и кладем на шестое место. Таким образом, при выкладывании карточек можно получить 720 различных шестизначных чисел.

Ответ: 720.

Замечание 1. В задаче мы рассмотрели 6 пронумерованных карточек и установили, что количество способов выкладывания этих карточек в ряд равно 6!

Если бы у нас было n пронумерованных карточек, то количество способов выкладывания их в ряд равнялось бы n!.

Замечание 2. Каждое расположение n пронумерованных карточек в ряд является перестановкой из n элементов, к изучению которых мы сейчас и переходим.

Определение 1. Пусть n – натуральное число. Рассмотрим произвольное множество, содержащее n элементов. Говорят, что на этом множестве задано упорядочение (отношение порядка), если его элементы пронумерованы числами 1, 2, 3, …, n.

Множество с заданным упорядочением называют упорядоченным множеством.

Определение 2. Рассмотрим множество, содержащее n элементов. Перестановкой из n элементов называют любое упорядочение этого множества.

Число перестановок из n элементов обозначают символом P_n.

В соответствии с Замечанием 1, справедлива формула: P_n = n!

В частности, P ₆ = 6! = 720.

Замечание 3. Введенные в данном разделе перестановки называют также перестановками без повторений.

Размещения

Рассмотрим следующую задачу.

Задача. 9 карточек пронумерованы числами 1, 2, 3, 4, 5, 6, 7, 8, 9. Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

Решение. Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует9·8=72способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует9·8·7=504способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует9·8·7·6=3024различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можнополучить 3024 различных четырехзначных числа.

Ответ: 3024.

При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

Определение 1. Рассмотрим множество, содержащее n элементов, и все его упорядоченные подмножества, содержащие k элементов. Каждое из этих подмножеств называют размещением из n элементов по k элементов.

Если обозначить символом 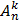число размещений из n элементов по k элементов, то будет справедлива формула:

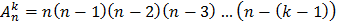
В соответствии с определением факториала, формулу (1) можно также записать в виде: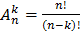

В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.

Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число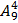

В соответствии с формулой (1), 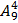 =9(9-1)(9-2)(9-3)=3024

что и было получено в задаче.

Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

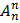 =n(n-1)(n-2)(n-3)…(n-(n-1))=1·2·3·4…·n,

смысл которой заключается в следующем.

Утверждение. Размещение из n элементов по n элементов является перестановкой из n элементов.

Сочетания

Определение 2. Рассмотрим множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называют сочетанием из n элементов по k элементов.

Задача.

Задача.

Ответ: 210.

Решить задачи:

Факториалы

Для произвольного натурального числа n формулаn!=1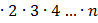

определяет факториал числа n (n! читается, как n – факториал).

Например, 5!=1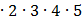

Считается, что0! = 1, 1! = 1.

Перестановки

Рассмотрим следующую задачу.

Задача. 6 карточек пронумерованы числами 1, 2, 3, 4, 5, 6. Карточки наугад выкладываем в ряд. Сколько при этом можно получить различных шестизначных чисел?

Решение. Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое, пятое, шестое. На первое место можно положить одну из 6 карточек. Для этого есть 6 способов. В каждом из этих 6 способов на второе место можно положить одну из оставшихся 5 карточек. Таким образом, существует6·5=30способов, чтобы положить карточки на первое и второе места. В каждом из этих 30 способов на третье место можно положить одну из оставшихся 4 карточек. Следовательно, существует 6·5·4=120 способов, чтобы положить карточки на первое, второе и третье места. В каждом из этих 120 способов на четвертое место можно положить одну из оставшихся 3 карточек. Отсюда вытекает, что существует 6·5·4·3=360 способов, чтобы положить карточки на первое, второе, третье и четвертое места. В каждом из этих 360 способов на пятое место можно положить одну из оставшихся 2 карточек. Следовательно, существует 6·5·4·3·2=720 способов, чтобы положить карточки на первое, второе, третье, четвертое и пятое места. После этого у нас остается одна единственная карточка, которую мы и кладем на шестое место. Таким образом, при выкладывании карточек можно получить 720 различных шестизначных чисел.

Ответ: 720.

Замечание 1. В задаче мы рассмотрели 6 пронумерованных карточек и установили, что количество способов выкладывания этих карточек в ряд равно 6!

Если бы у нас было n пронумерованных карточек, то количество способов выкладывания их в ряд равнялось бы n!.

Замечание 2. Каждое расположение n пронумерованных карточек в ряд является перестановкой из n элементов, к изучению которых мы сейчас и переходим.

Определение 1. Пусть n – натуральное число. Рассмотрим произвольное множество, содержащее n элементов. Говорят, что на этом множестве задано упорядочение (отношение порядка), если его элементы пронумерованы числами 1, 2, 3, …, n.

Множество с заданным упорядочением называют упорядоченным множеством.

Определение 2. Рассмотрим множество, содержащее n элементов. Перестановкой из n элементов называют любое упорядочение этого множества.

Число перестановок из n элементов обозначают символом P_n.

В соответствии с Замечанием 1, справедлива формула: P_n = n!

В частности, P ₆ = 6! = 720.

Замечание 3. Введенные в данном разделе перестановки называют также перестановками без повторений.

Размещения

Рассмотрим следующую задачу.

Задача. 9 карточек пронумерованы числами 1, 2, 3, 4, 5, 6, 7, 8, 9. Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

Решение. Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует9·8=72способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует9·8·7=504способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует9·8·7·6=3024различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можнополучить 3024 различных четырехзначных числа.

Ответ: 3024.

При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

Определение 1. Рассмотрим множество, содержащее n элементов, и все его упорядоченные подмножества, содержащие k элементов. Каждое из этих подмножеств называют размещением из n элементов по k элементов.

Если обозначить символом 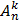число размещений из n элементов по k элементов, то будет справедлива формула:

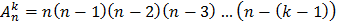
В соответствии с определением факториала, формулу (1) можно также записать в виде: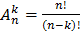

В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.

Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число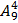

В соответствии с формулой (1), 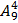 =9(9-1)(9-2)(9-3)=3024

что и было получено в задаче.

Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

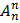 =n(n-1)(n-2)(n-3)…(n-(n-1))=1·2·3·4…·n,

смысл которой заключается в следующем.

Утверждение. Размещение из n элементов по n элементов является перестановкой из n элементов.

Сочетания

Определение 2. Рассмотрим множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называют сочетанием из n элементов по k элементов.

Число сочетаний из n элементов по k элементов

обозначается символом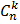

Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие k элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем k элементов (из определения 2), совершить всевозможные перестановки, количество которых равно k!, то мы получим все размещения.

Таким образом, справедлива формула: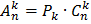

Следовательно, =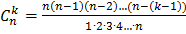

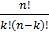
Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

1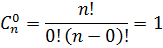
2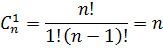
3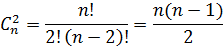
4
5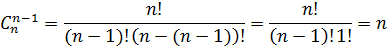
6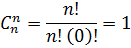

Решение задач:

Задача.