Муниципальное автономное общеобразовательное учреждение
Лицей ИГУ г. Иркутска (МАОУ Лицей ИГУ г. Иркутска)
Разработка учебного занятия на тему:
«Терема Фалеса»
Составитель программы: Ботоян Г.А.,
учитель математики МАОУ Лицей ИГУ
г. Иркутска.
Г. Иркутск, 2023
Тема урока: Теорема Фалеса. Обобщение теоремы Фалеса
Цель урока: Изучить теорему Фалеса, познакомиться с обобщением теоремы Фалеса, научиться решать задачи на основе данной темы урока.
Задачи:
Образовательные:
Дать формулировку и доказательство теоремы Фалеса, научиться применять теорему Фалеса при решении задач, вывести обобщение теоремы Фалеса, а также научиться решать задачи с помощью обобщенной теоремы Фалеса (теоремы о пропорциональных отрезках).
Развивающие:
Развить у учащихся интерес к геометрии, память, внимательность, продолжать развивать умение грамотно говорить, говорить четко и, по существу. Развить у учащихся внимательность, а также творческие способности.
Воспитательные:
Воспитывать у учащихся целеустремленность и самостоятельность в ходе решения задач. Прививать культуру устной речи.
Тип урока: урок изучения нового материала
Планируемые образовательные результаты:
Предметные:
Уметь применять теорему Фалеса, обобщенную теорему Фалеса.
Метапредметные:
Уметь планировать путь достижения целей, соотносить свои действия с планируемыми результатами; Уметь грамотно скорректировать и оценить план поставленной задачи.
Личностные:
Оценивать свои достижения и стремиться преодолевать трудности.
Оборудование: Интерактивная доска, проектор
Ход урока:
1) Организационные моменты:
· Готовность учащихся к работе
· Приветствие
2) Актуализация, формулировка темы урока и постановка цели и задач:
В курсе математики 8 класса существует такая теорема как: «Теорема Фалеса». В классическом учебники геометрии за 7 – 9 класс на эту теорему отведена всего одна задача, данная теорема даже не выносится как «важная» теорема геометрии. Однако при дальнейшем изучении курса геометрии, вам будут неоднократно попадаться задачи, связанные с теоремой Фалеса, либо с её обобщением.
Запишем тему сегодняшнего урока: «Теорема Фалеса. Обобщенная теорема Фалеса».
Давайте поставим перед собой следующие задачи:
1) Познакомиться с формулировкой теоремы Фалеса
2) Привести доказательство данной теоремы
3) Вывести формулировку обобщенной теоремы
4) Закрепить полученные знания при решении задач
3) Объяснение нового материала:
Запишем формулировку теоремы Фалеса:
Теорема
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки (рис. 1а, 1б).
Проиллюстрируем как выглядит данная теорема с точки зрения геометрии, используя программу GeoGebra (рис. 1а, 1б).
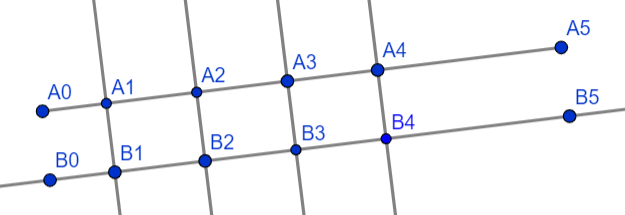
Рисунок 1а.
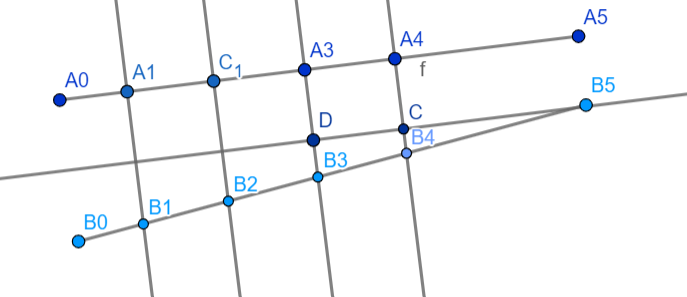
Рисунок 1б.
Давайте докажем данную теорему, а после приведем несколько примеров решения задач.
Данная теорема имеет довольно простое доказательство и включает в себя рассмотрение двух случаев:
1) Случай, когда прямые f1 и f2 параллельны (рис. 1а)
2) Случай, когда прямые f1 и f2 не параллельны (рис. 1б)
В случае, когда прямые параллельны, доказательство основывается на том, что отрезки A1A2 = B1B2 и A2A3 = B2B3 как противолежащие стороны параллелограммов (по условию задачи отрезки: A1A2, A2A3, …, равны; отрезки A1B1, A2B2, A3B3, …, параллельны). Так как A1A2 = A2A3 то и B1B2= B2B3.
В случае, когда прямые не параллельны (рис. 1б), необходимо провести прямую, параллельную прямой f1, а также проходящую через точку B5. После этого, используя ранее доказанную теорему Фалеса для двух параллельных прямых, несложно доказать данную теорему и для не параллельных.
При знакомстве детей с данной теоремой, также необходимо обратить их внимание на тот факт, что обратное теореме утверждение не является верным. Нельзя в общем случае утверждать, что если некоторые прямые пересекают две данные прямые и отсекают на каждой из них равные отрезки, то исходные прямые между собой параллельны
После доказательства теоремы, приведем примеры решения задач на изученную тему, для её закрепления:
Задача 1.
Дан параллелограмм ABCD (рис. 2). Точки K и F являются серединами сторон AB и CD соответственно. AC диагональ параллелограмма, точки E и O являются точками пересечения диагонали AC с отрезками KD и BF. Необходимо доказать, что отрезки, на которые точки E и O делят диагональ параллелограмма равны.
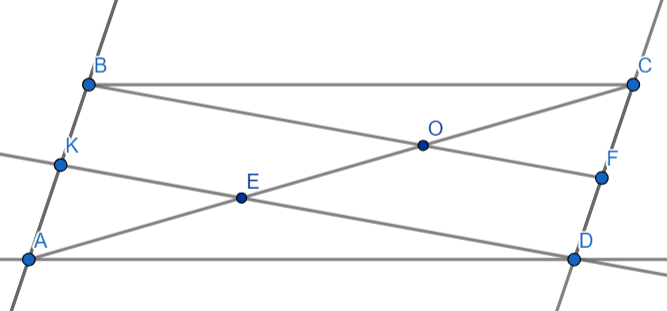
Рисунок 2.
Доказательство
1) По свойствам параллелограмма, AB = CD, AB ∥ CD. Тогда , KB = 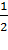 AB =
AB = 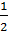 CD = FD. Значит, по признаку, BKFD параллелограмм. И, по свойству параллелограмма, BF ∥ KD.
CD = FD. Значит, по признаку, BKFD параллелограмм. И, по свойству параллелограмма, BF ∥ KD.
2) Рассмотрим прямые AB и AO и секущие KE и BO. Так как AK = KB (по условию), то AE = EO (по теореме Фалеса).
3) Рассмотрим прямые AC и CD и секущие OF и ED. Так как CF = FD (по условию), то CO = OE (по теореме Фалеса).
4) Из (2) и (3) следует, что AE = EO = OC.
Что и требовалось доказать.
Данный пример иллюстрирует практическое применение теоремы, на темах, которые ученики проходят в 8 классе. Также, после решения задачи учениками, можно построить чертеж задачи в программе
GeoGebra. Такой подход к обучению поможет лучше запомнить и понять детям материал и сделает урок более интересным.
Рассмотрим еще одну задачу, которая включает в себя не только теорему Фалеса, но и тему площадей многоугольников.
Задача 2.
На стороне AD прямоугольника ABCD, построен треугольник ADE так, что его стороны AE и DE пересекают отрезок BC в точках M и N, причем точка M середина отрезка AE. Докажите, что площадь прямоугольника ABCD равна площади треугольника ADE (рис. 3).
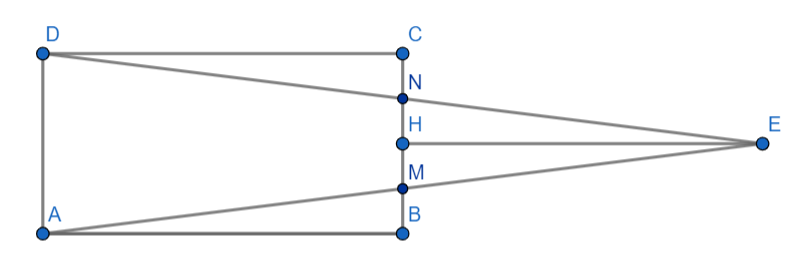
Рисунок 3.
Доказательство
1) Рассмотрим прямоугольник ABCD. Площадь данного прямоугольника можно составить суммы площадей треугольников ABM, DCN, а также из площади трапеции ADNM (NM ∥ AD, т.к. ABCD – прямоугольник). Рассмотрим треугольник ADE, его площадь можно найти из суммы площади трапеции ADMN и площади треугольника NME. Заметим, что в состав площади прямоугольника ABCD, также, как и в состав площади треугольника ADE, входит трапеция ADNM. Отсюда следует, что для доказательства равенства площадей ABCD и ADE, необходимо доказать, что площадь треугольника NME равна сумме площадей треугольников DCN и ANB.
2) Из вершины E, проведем высоту EH к стороне NM, треугольника NME. Заметим, что треугольник AMB равен треугольнику MHE по гипотенузе и острому углу в прямоугольных треугольниках. (AM = ME по условию, угол ABM равен углу MHE, равны 900, угол AMB равен углу HME как вертикальные).
3) Т.к. прямая AD ∥ CB, AM = ME, то по теореме Фалеса, прямая DN = NE. Отсюда следует, что треугольник DCN = треугольнику NHE (доказательство аналогично с пунктом (2)).
4) Из (2) и (3) следует, что SDCN + SAMB = SNME, отсюда следует, что SABCD = SADE.
Что и требовалось доказать.
Рассмотренные примеры показывают, как применяется теорема Фалеса при решении различных геометрических задач, но более практичное применение данной теоремы раскрывается при рассмотрении теоремы о пропорциональных отрезках, которая обычно не рассматривается в курсе 8 класса.
Теорема о пропорциональных отрезках
Рассмотрим следующую задачу:
В треугольнике ABC проведена медиана BM. Точка O - середина медианы BM; точка K - точка пересечения AO и BC. Найдите BK, если KC = 5. (рис.4а). Попробуем решить данную задачу с использованием теоремы Фалеса.
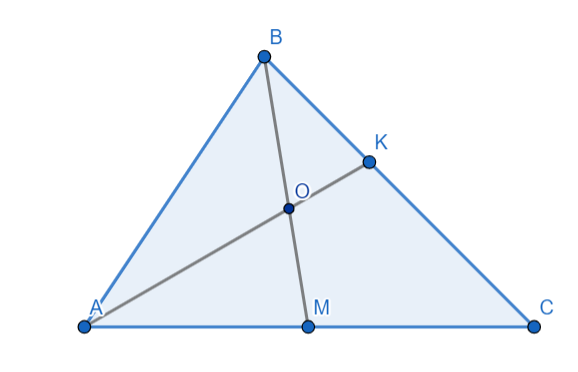
Рисунок 4а.
Решение
1) Проведем дополнительные построения:
Проведем прямую ME такую, что ME ∥ OK, точка E принадлежит BC. (рис. 4б)
Тогда для прямых AC и BC и секущих ME и AK, имеем следующие соотношения:
Т.к. AM = MC (по определению медианы), то KE = EC (по теореме Фалеса). Для того, чтобы решить задачу, нам необходимо получить отношение отрезков. Нам известно, что медиана делит сторону на две равные части, значит AC: AM = 2:1. Также по условию задачи нам известен отрезок KC, т.е. нам необходимо составить такое отношение сторон, при котором будет возможно найти отрезок KE. Если мы найдем отрезок KE, то нам будет известен и отрезок EC, а значит, по теореме Фалеса, не составит труда найти и искомый отрезок BK.
Можно ли утверждать, что AC:AM = KC:KE?
На самом деле да. В этом нам поможет обобщенная теорема Фалеса или теорема о пропорциональных отрезках.
По теореме о пропорциональных отрезках следует, что KC: KE = AC: AM. Значит: 5:x = 2:1. Получаем, что KE = EC = 2,5.
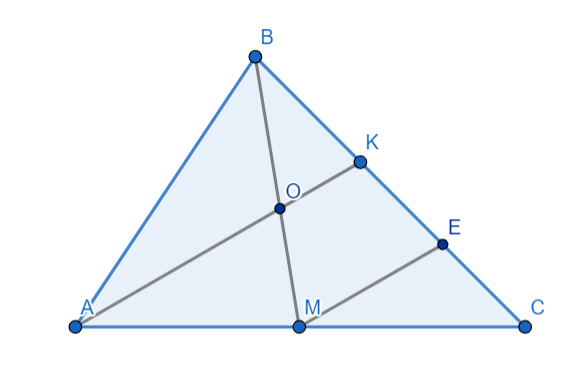
Рисунок 4б.
2) Рассмотрим прямые BC и BM и секущие ME и OK. По теореме Фалеса: т.к. BO = OM (по условию), то BK = KE, значит BK = 2,5. Ответ: BK = 2,5.
После решения задачи, давайте подробнее познакомимся с новой теоремой, которая возникла при решении задачи.
Сформулируем обобщенную теорему Фалеса (теорему о пропорциональных отрезках).
Теорема
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. (рис. 5)
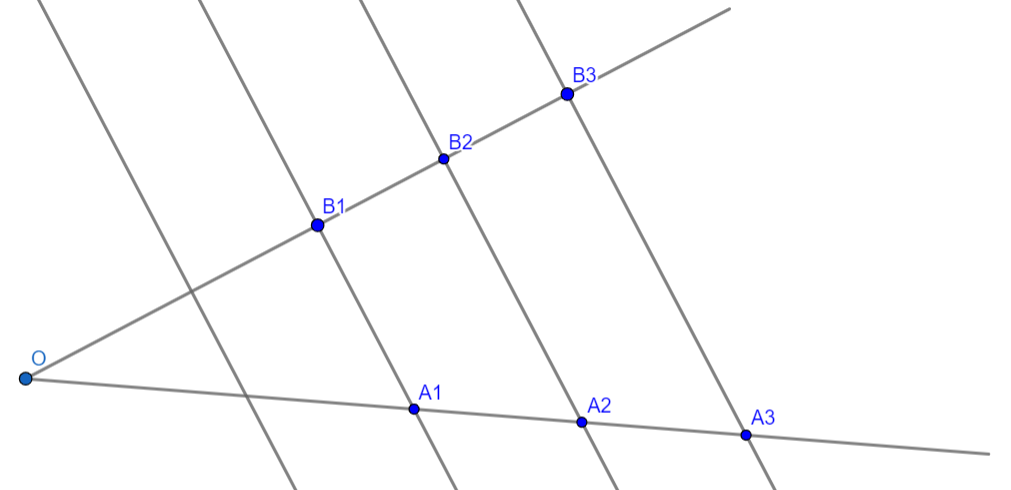
Рисунок 5.
OA1:OA3 = OB1:OB3, при условии, что A1 B1 ∥ A3 B3. Доказательство данной теоремы основывается на идее «от обратного». Т.е. необходимо допустить, что равенство неверно, например, пусть OA1:OA3 < OB1:OB3. Также на одном из лучей необходимо отложить такой отрезок, чтобы равенство достигалось. В ходе некоторых преобразований получим противоречия и теорема будет доказана.
Поскольку урок длится всего 40 минут, то полное доказательство данной теоремы затронуто не будет, рассказана основная идея, доказательство пойдет на дом как дополнительное задание.
Также данную теорему можно сформулировать и записать иначе:
Параллельные прямые отсекают на секущих пропорциональные отрезки:
A 1 A 2 : B 1 B 2 = A 2 A 3 : B 2 B 3
В заключении рассмотрим ещё одну задачу, решение которой затрагивает теорему о пропорциональных отрезках, в виде, указанном выше.
Задача
Рассмотрим классическую задачу геометрии об отношении медианы треугольника.
Докажите, что медианы треугольника делятся в отношении 2:1, считая от вершины. (рис.6)
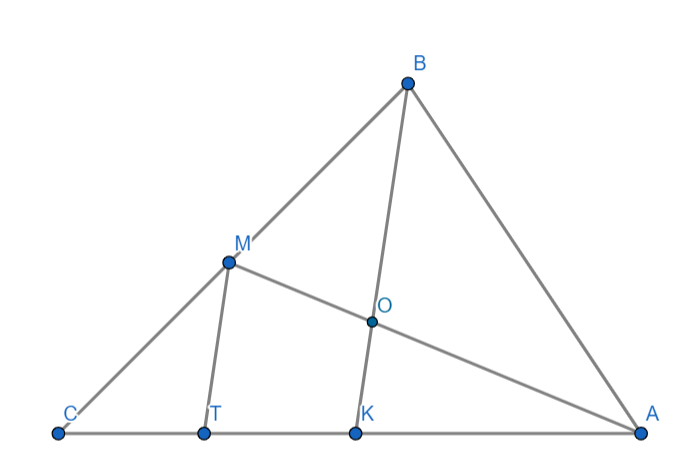
Рисунок 6.
Доказательство
Даны медианы треугольника AM и BK, O – точка пересечения медиан. Докажем, что BO: OK = AO:OM = 2:1.
1) Проведем отрезок MT, параллельный медиане BK (точка T лежит на стороне AC). Так как BM = MC (по определению медианы), то по теореме Фалеса: KT = TC.
2) AK = KC (по определению медианы), значит AK = KC =2KT, по теореме о пропорциональных отрезках следует, что AO: AK = OM: KT. Из данного соотношения следует, что AO:OM = AK: KT = 2. Аналогично доказывается отношение отрезков других медиан данного треугольника.
Что и требовалось доказать.
Итог урока
В ходе урока были изучены такие теоремы как: Теорема Фалеса, обобщенная теорема Фалеса (теорема о пропорциональных отрезках). Были рассмотрены задачи на данную тему, описано доказательство теоремы Фалеса. Цель и задачи урока были достигнуты.
Подводя итоги можно сказать, что данная тема является очень интересной и полезной при изучении курса геометрии, поэтому проведение данного урока считаю целесообразным, а также необходимым.






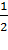 AB =
AB = 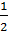 CD = FD. Значит, по признаку, BKFD параллелограмм. И, по свойству параллелограмма, BF ∥ KD.
CD = FD. Значит, по признаку, BKFD параллелограмм. И, по свойству параллелограмма, BF ∥ KD.







