Теория:

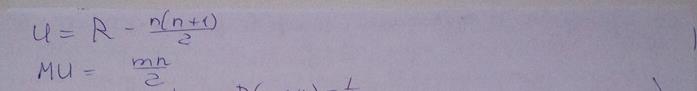
Практика в R:
myx <- read.table("C:\\Users\\Roman\\Desktop\\Education\\R\\data.txt", header=TRUE, fill=TRUE);
qqnorm(myx$MYXA30)
qqnorm(myx$MYXA60)
qqnorm(log(myx$MYXA30))
qqnorm(log(myx$MYXA60))
t.test(log(myx$MYXA30),log(myx$MYXA60)) # Средние не отличаются статистически
#См. 18 вопрос.
wilcox.test(myx$MYXA30, myx$MYXA60, pair = FALSE, alt = "two.sided") #Манна-Уитни - критерий Уилсона использующий ранговые суммы
Wilcoxon rank sum test with continuity correction
data: myx$MYXA30 and myx$MYXA60
W = 121, p-value = 0.8061
Alternative hypothesis: true location shift is not equal to 0
Задача о сравнении центров распределения в нескольких выборках при неизвестных законах распределения. Критерий Краскалла – Уоллиса. Работа с критерием в пакете R.
Теория:


Практика в R:
x = c(2.4,3.8,1.3,2.5,1.1,2.2,3.9, 3.1,3.4,2.6,3.8,4.1,1.7, 1.5,3.8,4.3,2.1,4.6,4.4,2.5,2.0);
grp = rep (c('SOWI', 'TNF', 'REWI'), c(7, 6, 8)); #повторяем первый вектор столько раз, сколько записано на той же позиции во 2 векторе
d = data.frame(x, grp)
bp = boxplot(x ~ grp, d)
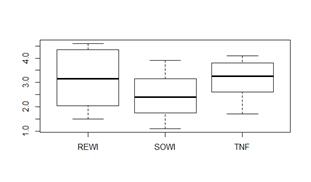
kruskal.test(x ~ grp, d)
Kruskal-Wallis rank sum test
Data: x by grp
Kruskal-Wallis chi-squared = 1.712, df = 2, p-value = 0.4249
Таблицы сопряженности признаков. Критерий независимости хи-квадрат для проверки независимости двух переменных. Оценки максимального правдоподобия при нулевой гипотезе. Работа с критерием в пакете R.
Теория:

Практика в R:
tab = matrix(c(2161, 3577, 2184, 1636, 2755, 5081, 2222, 1052, 936, 1753, 640, 306, 225, 419, 96, 38, 39, 98, 31, 14), ncol=4, byrow=T)
chisq.test(tab)
Pearson's Chi-squared test
Data: tab
X-squared = 568.57, df = 12, p-value < 2.2e-16
Непараметрические критерии независимости. Ранговый критерий независимости Спирмена. Работа с критерием в пакете R.
Теория:
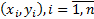
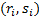 , где
, где 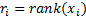 среди всех x,
среди всех x, 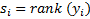 среди всех y.
среди всех y.
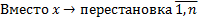
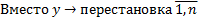
Если гипотеза о независимости имеет место, т.е.:
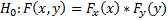
тогда имеем две независимые на удачу взятые перестановки.
Можно вычислить ковариацию между рангами:
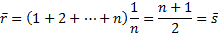
Ранговая корреляция Спирмена:
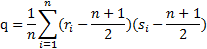
(выборочная ковариация)
При 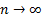 распределение
распределение 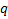 стремится к нормальному.
стремится к нормальному.
Практика в R:
cor.test(trees$Volume, trees$Girth, method='spearman')
Spearman's rank correlation rho
data: trees$Volume and trees$Girth
S = 224.61, p-value < 2.2e-16
Alternative hypothesis: true rho is not equal to 0
sample estimates:
Rho
0.9547151
Непараметрические критерии независимости. Критерий независимости Фишера. Работа с критерием в пакете R.
Теория:

Практика в R:
tab = matrix(c(1, 8, 10, 4), ncol=2, byrow=T)
fisher.test(tab)
Fisher's Exact Test for Count Data
Data: tab
p-value = 0.009423
Alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.001034782 0.656954980
sample estimates:
Odds ratio
0.05851868
Модель Гаусса – Маркова простой линейной регрессии. Оценка параметров и анализ остатков. Решение данных задач в пакете R.
Теория:
Регрессия – отыскание функциональной зависимости между переменными при неслучайных входах 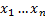 .
.
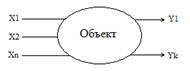
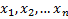 – объясняющие, независимые переменные
– объясняющие, независимые переменные
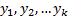 – выходные, зависимые переменные, отклик на воздействие
– выходные, зависимые переменные, отклик на воздействие
Пусть все переменные – числовые
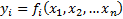 ,
, 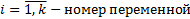
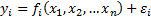 ,
, 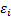 - погрешность
- погрешность
1. МНК и интерполяция. При неслучайных входных данных 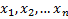
2. x,y – случайные величины
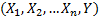 – случайный вектор
– случайный вектор
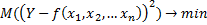
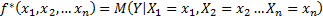 – уравнение регрессии Y на
– уравнение регрессии Y на 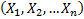
Пример
X – рост отца
Y – рост сына
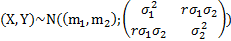
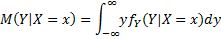
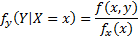
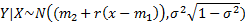
( 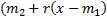 – линейная функция от x)
– линейная функция от x)
Модель Гаусса-Маркова
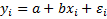 ,
, 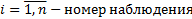
(1 вход и 1 выход)
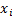 – неслучайная величина
– неслучайная величина
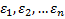 – н.о.р.
– н.о.р. 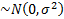
Неизвестные параметры 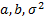
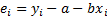 – наблюдаемые погрешности
– наблюдаемые погрешности




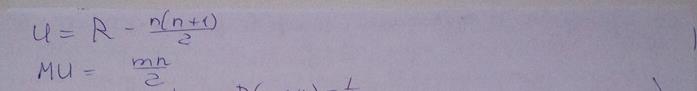




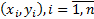
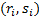 , где
, где 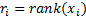 среди всех x,
среди всех x, 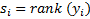 среди всех y.
среди всех y.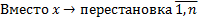
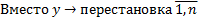
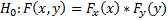
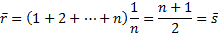
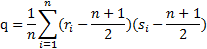
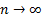 распределение
распределение 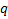 стремится к нормальному.
стремится к нормальному.
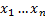 .
.
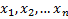 – объясняющие, независимые переменные
– объясняющие, независимые переменные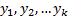 – выходные, зависимые переменные, отклик на воздействие
– выходные, зависимые переменные, отклик на воздействие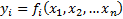 ,
, 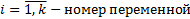
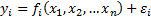 ,
, 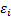 - погрешность
- погрешность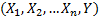 – случайный вектор
– случайный вектор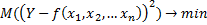
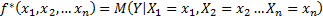 – уравнение регрессии Y на
– уравнение регрессии Y на 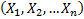
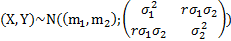
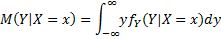
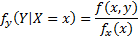
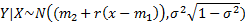
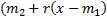 – линейная функция от x)
– линейная функция от x)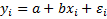 ,
, 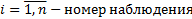
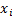 – неслучайная величина
– неслучайная величина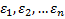 – н.о.р.
– н.о.р. 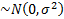
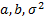
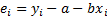 – наблюдаемые погрешности
– наблюдаемые погрешности


