Экспоненциальное гаммирование

Крокодил Гена и Чебурашка

Крокодил Гена посылает Чебурашке по радиоканалу сообщение, заменяя его

буквы наборами из нулей и единиц согласно табл.1 (другие буквы не встретились).

 

Из-за помех некоторые биты исказились, но не более двух в одном наборе.

Определите, какое сообщение отправил крокодил Гена, если Чебурашка получил:

Решение:

По условию задачи в каждом наборе искажено не более двух бит. Заметим, что наборы из табл. 1, соответствующие различным буквам, отличаются по крайней мере в трех позициях. Отсюда следует, что искажение одного или двух битов в любом наборе из табл. 1, не делает его другим набором из табл. 1 (на это потребовалось бы по крайней мере три искажения). Значит все те наборы из письма Гены, которые соответствуют наборам из табл. 1, просто не были искажены. Выпишем, соответствующие им буквы:                                     УД*Р*А*Т*Р**Т*И*Т*С*Ч*Д*У*ИХ*Д*Р**

(“*” отмечены пока не известные буквы). Итак, уже имеется некоторая основа сообщения, которая поможет нам подобрать остальные буквы. Для восстановления третьей буквы требуется посмотреть, какие наборы из табл. 1 могли при искажении одного/двух битов стать набором (0,0,1,0,0,0,0), и выбрать тот набор, которому соответствует буква, подходящая по смыслу. Так, набор (0,0,1,0,0,0,0) мог быть получен из набора (0,0,0,0,0,0,0) (при искажении третьего бита) или из набора (1,0,1,0,0,1,0) (при искажении первого и седьмого битов) или из набора (0,0,1,1,0,0,1) (при искажении четвертого и седьмого битов). Очевидно, что по смыслу подходит только набор (0,0,0,0,0,0,0), соответствующий букве А. Аналогичным образом восстанавливаются остальные неизвестные буквы. В результате, получаем письмо Гены.

УДАР МАСТЕРА СТОИТ ТЫСЯЧИ ДРУГИХ УДАРОВ.

Экспоненциальное гаммирование

Для зашифрования сообщения на русском языке, записанного без знаков препинания и пробелов, используется последовательность натуральных чисел x1, x2,..., удовлетворяющая соотношению: xk = b·8a(k-1), k = 1, 2,... Здесь a и b - фиксированные (но неизвестные) натуральные числа. Зашифрование производится следующим образом. Первую букву сообщения заменяют числом согласно таблице 1 и складывают с x1. Потом также заменяют вторую букву и складывают с x2 и т.д.

Затем все полученные суммы заменяют остатками от деления на 31, а остатки заменяют буквами согласно таблице 2.

В результате получился текст:

Ояфпрпяфбкпщсьижьияысязтхжутнажбсёнфвгмнутуёшжфн

Найдите исходное сообщение, представляющее собой отрывок известного стихотворения, если известно, что в нем есть слово равнины.

Я завтра уезжаю в Санкт-Петербург на две недели. Пароль: Бургундия

Нечитаемый пароль

Для доступа к общему почтовому ящику в Интернете Катя и Юра пользуются паролем СВЕЧА. Катя решает сменить этот пароль на новый (осмысленное слово русского языка из пяти букв). Новый пароль передается по сети Юре в зашифрованном виде. Зашифрование осуществляется так. Первые буквы нового и старого пароля заменяются числами согласно таблице

 Затем эти числа складываются, а полученная сумма заменяется остатком от деления на 33. Таким же образом поступают со вторыми буквами паролей, затем с третьими и т.д. После расшифрования Юра получил нечитаемый пароль из английских букв: SARCL. Оказалось, что программа расшифрования Юры была настроена на работу с английским алфавитом. При этом перед расшифрованием программа заменяла числовые значения поступившего зашифрованного пароля и старого пароля остатками от деления на 26, а расшифрование заключалось в нахождении их разностей (к отрицательной разнице прибавлялось число 26), которые приводились к буквенному виду согласно таблице   

Помогите Юре понять, какой новый пароль установила Катя.

Решение:

 

Ответ:

ШАРИК

 

Шифр Виженера

Осмысленная фраза на русском языке записана два раза подряд без пробелов и знаков препинания и зашифрована шифром Виженера. Зашифрование состоит в следующем. Выбирается ключевое слово, например, мир. Для изменения первой буквы шифруемого сообщения создается таблица следующего вида:

 

В нижней строке алфавит циклически сдвинут влево так, чтобы первая буква ключевого слова м оказалась под буквой а. Буква открытого текста (например, п) отыскивается в верхней строке и заменяется стоящей под ней буквой (для п – это ь). Для зашифрования второй буквы аналогичным образом используется буква и, третьей - р, четвертой – вновь м и т.д.

Сообщение было зашифровано с использованием ключевого слова из пяти букв. Результат зашифрования выглядит так:

Поворотная решетка - 3

Сообщение на русском языке, состоящем из 63 букв и восклицательного знака, зашифровано с использованием так называемой «поворотной решетки», которая представляет собой трафарет, изготовленный из квадратного листа клетчатой бумаги 8 на 8. трафарете вырезаны 16 клеток. Одна сторона трафарета помечена. При наложении трафарета на чистый лист бумаги четырьмя возможными способами (помеченной стороной вверх, вправо, вниз, влево) его вырезы полностью покрывают всю площадь квадрата, причем каждая клетка оказывается под вырезом ровно один раз. Буквы сообщения построчно сверху вниз и слева направо вписываются в вырезы трафарета (пробелы между словами игнорируются). После заполнения всех вырезов буквами сообщения трафарет располагается в следующем положении и т.д. Результат зашифрования сообщения представлен на рисунке. Найдите исходное сообщение

 

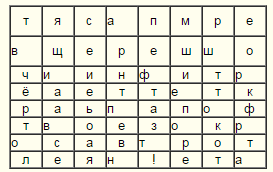
Решение:

Для решения этой задачи участникам потребовалось проявить наблюдательность. При рассмотрении рисунка видно, что большинство букв расположено точно в центре клетки, а часть букв – смещена. Если выделить смещенные буквы, как это сделано на рисунке, сможем прочитать фрагмент текста авшифреповоротна.

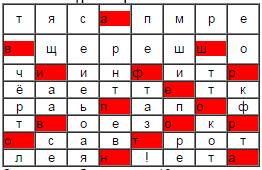
Ответ:

Смещение трафарета в шифре поворотная решетка позволяет прочитать текст!

 

Периодическая гамма-2

Сообщение зашифровано следующим образом. Над буквами сообщения надписывается числовая последовательность, образованная периодическим повторением 6 цифр, образующих дату. Например, шестерка 181107 отвечает дате 18 ноября 2007 года. После этого буквы сообщения заменяются буквой алфавита, циклически отстоящей от нее справа на число букв, указанное цифрой над ней. Можно ли прочитать зашифрованное таким образом сообщение

Т П И Ё Р Ж Е М А А С Ф С Г Ь О Г Х Ж П Н,

если неизвестна дата его написания?

Решение:

Тот факт, что используемые для зашифрования цифры отвечают некоторой дате, накладывает на них некоторые ограничения, например: первая цифра в дате – только 0,1,2 или 3, третья – только 0 или 1. Теперь под каждой буквой шифрованного текста подпишем возможные варианты исходных букв:

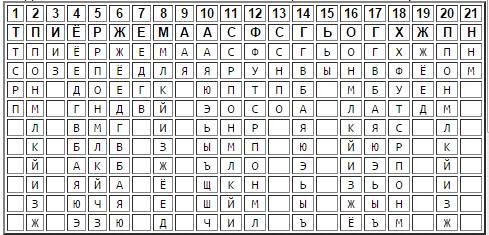
Исходное сообщение получается выбором одной буквы в каждом столбце исходя из соображений «читаемости». Например, в 15-м столбце присутствуют только буквы Ь и Ы, что сразу приводит к отсеву нижних семи вариантов букв в предыдущем столбце. Поскольку комбинация из шести цифр периодически повторялась, те же самые варианты отсеиваем во 2-м, 8-м и 20-м столбцах.

 

 

 

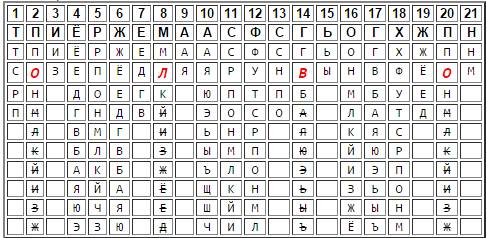
Теперь из первых двух столбцов видно, что единственным допустимым вариантом выбора буквы во втором столбце является буква О. Учитываем это наблюдение в 8, 14 и 20 столбцах. Теперь уже несложно подобрать исходное сообщение: ПОЗДРАВЛЯЮ С НОВЫМ ГОДОМ. Используемая дата – 31.12.2007.

 

Четверостишие-2

Каждая буква фрагмента известного стихотворения Ф.И. Тютчева заменена некоторой буквой так, что разным буквам соответствуют разные буквы, а одинаковым - одинаковые. Пробелы и знаки препинания сохранены. Восстановите этот фрагмент стихотворения:

Гьюь Фюббшн эй яюэовл,

Пфзшэюь юришь эй шчьйфшвл:

Г эйщ юбюрйээпо бвпвл -

С Фюббшн ьюцэю вюылъю сйфшвл.

Решение:

1. Рассмотрим фрагменты эй и эйщ; это — слова из 2 и 3 букв. Одно из слов имеет суффикс йээ. Весьма вероятно, что э заменяет букву н, а й — одна из гласных: о, а, и, е. Тогда возможными вариантами окончания слова юбюрйээпо являются следующие: онная, онные, енные, енная, инная, инные. Вариант окончания ные не подходит, так как при этом п заменяет ы, и с буквы ы начинается слово пфзшэюь. Поэтому п заменяет либо а, либо о.

2. Можно попытаться угадать слово бвпвл. В нем в — согласная. Комбинация вида xоx, где x — согласная, вряд ли возможна. Из вариантов xаx, где x — согласная, подходит, разве что тат. Проверим гипотезу: в заменяет т.

3. Замечаем, что 4 окончания слов — овл, швл, пвл, швл образуют рифму. С учетом шага 2, «напрашиваются» варианты окончаний ать, ить, ять.

4. ю часто встречается, скорее всего, это — гласная. Имеется фрагмент..юбб.. Так как буква н уже занята, удвоение бб — это, скорее всего, замена для сс, и юбб — это асс, осс, есс или исс. Возвращаясь к шагу 2, устанавливаем, что бвпвл — это стать.

5. Учитывая шаг 4, а также то, что с большой буквы начинается имя собственное, попытаемся угадать слово Фюббшн. «Напрашивается» вариант Россия, Россию, откуда находим, что ю заменяет о, а ш заменяет и.

6. Первое слово — Гьюь. Ясно, что ь — согласная. Возможны следующие слова из 4 букв: удод, скок, умом. Отсюда получаем первое предложение: Умом Россию не понять. Дальше легко догадаться.

 

Обход конем

Знаменитый математик Леонард Эйлер в 1759 г. нашел замкнутый маршрут обхода всех клеток шахматной доски ходом коня ровно по одному разу. Прочтите текст, вписанный в клетки шахматной доски по такому маршруту (см. рис.7). Начало текста в a4.

Решение:

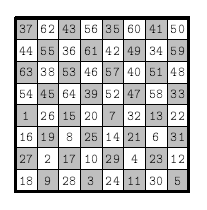
Кавалергардов век недолог

И потому так сладок он.

Труба трубит, откинут полог...

 

Перестановка столбцов

Сообщение было построчно записано в таблицу, имеющую 20 столбцов. При этом в каждую клетку таблицы записывалось по одной букве сообщения, пробелы между словами были опущены, а знаки препинания заменены на условные комбинации: точка - ТЧК, запятая - ЗПТ. Затем столбцы таблицы были некоторым образом переставлены, в результате чего был получен текст:

 

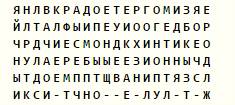
Прочтите исходное сообщение.

Решение:

Так как при записывании сообщения в таблицу пробелы опускались, можно сделать вывод, что столбцы, содержащие пробел в последней клетке, до перестановки стояли в конце таблицы. Таким образом, столбцы можно разбить на две группы, как показано на рис 1. При этом для получения исходного текста потребуется переставлять столбцы только внутри групп.

Естественно предположить, что сообщение оканчивалось точкой. Поэтому на третьем с конца месте в первой группе должен быть столбец, оканчивающийся на Т, на втором - на Ч, на последнем - на К. Получаем два варианта (рис.2), из которых первый является явно "нечитаемым".

Таким образом, удалось зафиксировать последние три столбца первой группы. Переставляя столбцы второй группы, ищем "читаемые" продолжения зафиксированных столбцов. Действуя далее аналогичным образом с оставшимися столбцами первой группы, достаточно легко получаем исходное сообщение.

Ответ:

Проверка телетайпа

Для проверки телетайпа, печатающего буквами русского алфавита А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я передан набор из 9 слов, содержащий все 33 буквы алфавита. В результате неисправности телетайпа на приемном конце получены слова

ГЪЙ АЭЁ БПРК ЕЖЩЮ НМЬЧ СЫЛЗ ШДУ ЦХОТ ЯФВИ

Восстановите исходный текст, если известно, что характер неисправности таков, что каждая буква заменяется буквой, отстоящей от нее в указанном алфавите не дальше, чем на две буквы. Например, буква Б может перейти в одну из букв {А, Б, В, Г}.

Решение:

Ответ: БЫК ВЯЗ ГНОЙ ДИЧЬ ПЛЮЩ СЪ Ë М ЦЕХ ШУРФ ЭТАЖ

Фраза на латыни

Зашифрование фразы на латинском языке осуществлено в два этапа. На первом этапе каждая буква текста заменяется на следующую в алфавитном порядке (последняя Z заменяется на первую A). На втором этапе применяется шифр простой замены с неизвестным ключом. Его применение заключается в замене каждой буквы шифруемого текста буквой того же алфавита, при этом разные буквы заменяются разными буквами. Ключом такого шифра является таблица, в которой указано, какой буквой надо заменить каждую букву алфавита.

По данному шифртексту

OSZJX FXRE YOQJSZ RAYFJ

восстановите открытое сообщение, если известно, что для использованного (неизвестного) ключа результат шифрования не зависит от порядка выполнения указанных этапов для любого открытого сообщения. Пробелы в тексте разделяют слова.

Латинский алфавит состоит из следующих 24 букв:

A B C D E F G H I J L M N O P Q R S T U V X Y Z.

Решение: Занумеруем буквы латинского алфавита последовательно числами от 1 до 24. Пусть x - некоторое число от 1 до 24, а f(x) - число, в которое переходит x на втором этапе. Тогда перестановочность этапов можно записать в следующем виде:

f(x+1) = f(x) + 1, т. е. f(x+1) - f(x) = 1.

Это означает, что соседние числа x и x+1 на втором этапе переходят в соседние же числа f(x) и f(x+1), т. е. второй этап - тоже сдвиг. Последовательное применение двух сдвигов - очевидно тоже сдвиг и остается рассмотреть 24 варианта различных сдвигов. Читаемый текст определяется однозначно. Осложнения, связанные с переходом Z в A, устраняются либо переходом к остаткам при делении на 24, либо выписыванием после буквы Z второй раз алфавита AB... Z.

Четверостишие

Криптограмма

12 2 24 5 3 21 6 29 28 2 20 18 20 21 5 10 27 17 2 11 2 16 -

19 2 27 5 8 29 12 31 22 2 16, 19 2 19 5 17 29 8 29 6 29 16:

8 2 19 19 29 10 19 29 14 19 29 29 19 10 2 24 2 11 2 16

10 14 18 21 17 2 20 2 28 29 16 21 29 28 6 29 16.

получена заменой букв на числа (от 1 до 32) так, что разным буквам соответствуют разные числа. Отдельные слова разделены несколькими пробелами, буквы - одним пробелом, знаки препинания сохранены. Буквы "е" и "ё" не различаются. Прочтите четверостишие В. Высоцкого.

Решение:

Один из вариантов решения состоит из следующих этапов.

1. 19=н из второй строки ("19,2 19,5").

2. 29=о из третьей строки ("29,н,10") и 10=а или 10=и.

3. 14=щ из "но,14,но".

4. 8=д, 2=е, 10=и из "денно и нощно".

Получили текст:

Е 24 5 3 21 6 о 28 е 20 18 20 21 5 и 27 17 е 11 е 16 -

н е 27 5 д о 12 31 22 е 16, н е н 5 17 о д о 6 о 16:

И щ 18 21 17 е 20 е 28 о 16 21 о 28 6 о 16.

5. 5=а и 27=з из второй строки.

6. 17=в 6=п 16=й - последнее слово второй строки - водопой.

Получили текст:

Е 24 а 3 21 п о 28 е 20 18 20 21 а и з в е 11 е й -

н е з а д о 12 31 22 е й, н е н а в о д о п о й:

И щ 18 21 в е 20 е 28 о й 21 о 28 п о й.

7. 21=т 18=у 28=л 20=с из последней строки "ищут веселой толпой".

8. 11=р из "з в е 11 е й" первой строки.

Итак,

Колонки

Буквы русского алфавита занумерованы в соответствии с таблицей:

 

Для зашифрования сообщения, состоящего из n букв, выбирается ключ К - некоторая последовательность из n букв приведенного выше алфавита. Зашифрование каждой буквы сообщения состоит в сложении ее номера в таблице с номером соответствующей буквы ключевой последовательности и замене полученной суммы на букву алфавита, номер которой имеет тот же остаток от деления на 30, что и эта сумма.

Прочтите шифрованное сообщение: РБЬНТСИТСРРЕЗОХ, если известно, что шифрующая последовательность не содержала никаких букв, кроме А, Б и В.

Решение:

.

Поиск слова

При зашифровании текста на русском языке (в текстах строчные и заглавные буквы не различались, а пробелы и знаки препинания опускались) каждую букву заменяли парой цифр. При этом разные буквы текста заменялись разными парами, а одинаковые - одинаковыми. Найдите все возможные места расположения слова ПОДЪЕЗД в исходном тексте по шифрованному тексту:

92 97 36 72 97 92 70 73 97 90 97 72 38 39 74 76

97 34 79 78 97 70 76 74 72 74 73 74 76 70 70 97

76 74 96 74 37 39 75 97 70 39 74 79 39 37 71 74

98 35 94 90 98 97 94 96 74 98 74 76 97

Решение:

Из таблиц видно, что осмысленными являются варианты:

и.с.1 =     К    О    Г     Д     А    О    Т    .     .     .     .     .     .     .       К    О    Р     А    Б     Л    И

и.с.2 =     К    О    Р     А    Б     Л    И   .     .     .     .     .     .     .       В     Е     Ч    Е     Р     О    М

Ответ:

Естественно предположить, что в первом исходном сообщении речь идет об отплытии кораблей. Предположив, что неизвестным участком первого исходного сообщения является подходящая по смыслу часть слова ОТПЛЫВАЮТ, находим неизвестную часть второго исходного сообщения: слово ОТХОДЯТ.

 

Определение языка

Для зашифрования текстов каждую букву заменяли парой цифр. При этом разные буквы текста заменялись разными парами, а одинаковые - одинаковыми. Даны два зашифрованных текста:

79 92 38 98 95 91 34 95 73 77 96 92 78 95 73 98 92 96 92 72 98 96 77 72 92 34 77 96 75 90 76 95 38 98 92 70 33 90 96 79 90 96 77 98 95 90 38 77 70 70 90 98 74 92 96 98 96 77 72 92 34 77 96 75 73 77 96 92 98 74 92 79 96 90 79 92 96 98 94 90 76 98 74 92 95 96 96 92 73 79 92 33 98 95 32 92 90 93 38 92 96 73 94 90 91 96 91 73 92 98 74 95 73 33 72 96 90 34 95 73 73 91 36 71 92 33 98 98 90 77 38 92 38 72 91 73 92 96 70 95 33 92 38 33 92

71 75 74 39 74 73 74 72 30 73 74 78 33 79 98 94 78 36 79 97 72 29 78 74 96 74 92 30 38 79 70 72 94 78 79 22 92 92 79 98 37 70 92 74 94 77 74 93 31 78 74 70 39 79 71 75 94 98 70 39 97 92 72 22 23 39 78 94 70 74 76 78 94 78 78 30 77 39 94 74 75 94 39 79 38 94 70 73 79 77 79 78 39 94 75 94 70 73 75 74 76 94 39 74 96 74 76 78 74 96 79 94 39 79 71 30 27 39 79 32 71 75 74 39 74 73 74 72 74 92 71 75 94 98 35 22 92 72 22 23 39

Известно, что один из них соответствует сообщению на русском языке, а другой - на английском (в текстах строчные и заглавные буквы не различались, а пробелы и знаки препинания опускались). Определите, какой шифрованный текст соответствует сообщению на русском языке.

Решение: Для решения этой задачи достаточно было заметить, что при указанном способе зашифрования количество различных букв в исходном тексте совпадает с числом различных пар в криптограмме. Первая из приведенных в условии задачи криптограмм содержит 23 различные пары, а вторая — 29. Так как латинский алфавит состоит из 26 букв, английскому исходному тексту может соответствовать только первая криптограмма.

Пропуск букв

Для зашифрования текста v1v2...vk на русском языке каждую его букву vi заменили числом ti согласно таблице

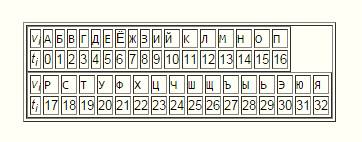
К каждому числу ti последовательности t1,t2,…,tk прибавили число ai последовательности a1,a2,…,ak, заданной соотношениями a1=1, an+1=3an+4 при n > 0. Затем остаток от деления каждой суммы ti+ai на 33 вновь заменили буквой по той же таблице. При переписывании зашифрованного текста несколько букв были пропущены. В результате получилось вот что:

Р Ч Ж Ь Э Т С Ъ Й Л Ж Ъ Я О Ш К С

Найдите исходный текст.

Решение:

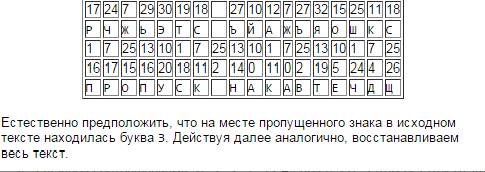
Гамма Фибоначчи

Для зашифрования сообщения используют последовательность неотрицательных целых чисел x1, x2,…, удовлетворяющую соотношению xk+3=xk+xk+2, k=1,2,… Две строки известного стихотворения, последние 5 букв которых совпадают, зашифровали следующим образом. Первую букву заменили числом согласно таблице

и сложили с x1, вторую заменили и сложили с x2 и т.д. Затем все суммы заменили остатками от деления на 31, а остатки заменили буквами согласно таблице. Получили текст

СЕЗНПБКЬЛЧЕЮЩЦТНИЭЛЬЩБШЬЕЮ

ЛУАЕЧЖЪЭШЭЛЪШЩХЧШДЮВЫЮИД.

Восстановите три буквы, соответствующие в таблице числам x1,x2,x3, и прочитайте двустишие.

Решение:

Обозначим a = x1, b = x2, c = x3. Так как эти числа соответствуют буквам в таблице, они принимают значения от 0 до 30. Из соотношения

xk+3 = xk + xk+2

последовательно получим

x1 = a,

x2 = b,

x3 =c,

x4 = a + c,

x5 = a + b + c,

x6 = a + b+ 2c,

x7 = 2a + b+ 3c,

x8 = 3a + 2b+ 4c,

x9 = 4a + 3b+ 6c,

x10= 6a + 4b+ 9c,

и т.д.

При дальнейшем построении этой последовательности используем следующие правила.

Для построения следующей строки последнюю строку складываем с предпредпоследней.

Легко заметить, что столбцы чисел отличаются сдвигом по вертикали, поэтому сначала можно определить только коэффициенты при c.

Так как нас интересуют только остатки от деления на 31, то, например, 41c = 31c + 10c можно заменить на 10c.

Продолжая аналогично, получим

x11 = 13,

x12 = 19,

x13 = 28,

x14 = 10,

x15 = 29,

x16 = 26,

x17 = 5,

x18 = 3,

x19 = 29,

x20= 3,

x21 = 6,

x22 = 6a + 3b+ 4c,

x23 = 7a + 4b+ 13c,

x25 = 13a + 7b+ 17c,

x26= 17a + 13b+ 24c,

x26= 6a + 4b+ 9c,

Используя сдвиги столбцов, получили значения x22, x23, x24, x25, x26. Продолжая аналогично, получим последние пять значений x46, x47, x48, x49, x50:

x27 = 6,

x28 = 23,

x29 = 16,

x30 = 22,

x31 = 14,

x32 = 30,

x33 = 21,

x34 = 4,

x35 = 3,

x36= 24,

x37 = 28,

x38 =0,

x39 = 24,

x40= 21,

x41 = 21,

x42 = 14,

x43 = 4,

x44= 25,

x45 = 8,

x46 = 8a + 25b+ 12c,

x47 = 12a + 8b+ 6c,

x48 = 6a + 12b+ 14c,

x49= 14a + 6b+ 26c,

x50= 26a + 14b+ 1c.

Итак, получено выражение чисел x22, x23, x24, x25, x26 и чисел x46, x47, x48, x49, x50 через a, b, c. Обозначим через Оi, Шi числа, соответствующие i-м буквам стихотворения и полученного шифрованного текста. Тогда числа О22+x22 и Ш22 имеют одинаковые остатки от деления на 31. То же самое и с числами О46+x46 и Ш46.

А так как числа О22 и О46 одинаковые, рассмотрев разности соответствующих частей, получим, что

x46 - x22 и Ш46 - Ш22 (*)

дают одинаковые остатки от деления на 31.

Последним пяти буквам первой строки шифрованного текста соответствуют следующие числа Шi:

Б, Ш, Ь, Е, Ю — 1, 23, 27, 5, 29,

а последним буквам второй строки — следующие:

В, Ы, Ю, И, Д — 2, 26, 29, 8, 4.

Подставляя эти значения в (*) и выражая xi через a, b, c, получаем систему

       2a − 9b + 8c = 1,

8a + 2b − c = 3,

−a + 8b + c = 2,

a − b + 9c = 3,

9a + b + 8c = 6,

где равенство означает равенство остатков от деления на 31. При этом использовали правило 3. Например, в первом уравнении +22b заменили на −9b. Осталось решить полученную систему. Складывая второе и третье, четвертое и пятое, третье и четвертое уравнения, получим

       7a + 10b = 5, (**)

10a + 17c = 9,

7b + 10c = 5.

Выразим b и c через a и подставим в первое уравнение:

b = (5 − 7a)/10, c = (9 − 10a)/17,

2a − 9((5 − 7a)/10) + 8((9 − 10a)/17) = 1,

340a − 9·17(5 − 7a) + 80(9 − 10a) = 170,

611a = 215,

22a = 29.

Последнее уравнение можно решить методом подбора и обнаружить, что 22 ·14 и 29 дают одинаковые остатки от деления на 31. Итак,

a=14.

Из системы (**) находим, что 10b = 0 и 10с = 5, откуда

b=0,

c=16.

Зная a, b, c, можно последовательно найти все xi и из соотношения Oi=Шi-xi получить стихотворение:

ВЕЧОРТЫПОМНИШЬВЬЮГАЗЛИЛАСЬ

НАМУТНОМНЕБЕМГЛАНОСИЛАСЬ

Короткое замыкание

Порядковый номер каждой буквы алфавита русского языка, состоящего из 32 букв (Е и Ё отождествлены), представлен в двоичной системе счисления пятизначным числом, начиная с нуля. Например, букве А соответствует двоичное число 00000, а букве Ч - 10111. Передача каждой буквы сообщения осуществляется путем передачи каждой из цифр соответствующего пятизначного двоичного числа по отдельному проводу. Криптоша случайно замкнул какие-то два из этих пяти проводов. В результате на других концах замкнутых проводов появляется 1, как только по одному из них передается 1. Найдите переданное слово, если получен текст ТЕЫЕУТАЦ.

Решение: Запишем полученное сообщение в двоичном виде:

Т 1     0     0     1     0

Е 0     0     1     0     1

Ы 1     1     0     1     1

Е 0     0     1     0     1

У 1     0     0     1     1

Т 1     0     0     1     0

А 0     0     0     0     0

Ц 1     0     1     1     0

Если провода замкнуты, то по ним передаются одинаковые символы (0 или 1), т.е. замкнутым проводам соответствуют одинаковые столбцы цифр. Легко видеть, что это первый и четвертый столбцы. Значит, во 2-м, 3-м и 5-м столбцах все символы правильные, кроме того, если в 1 и 4 столбцах стоят нули, то это тоже правильные знаки. Если в 1-м и 4-м столбцах стоят единицы, то возможны три варианта для знаков x и y этих столбцов:

1     0

0     1

1     1

Каждому варианту соответствует своя буква:

x     0     0     y     0

0     0     1     0     1

x     1     0     y     1

0     0     1     0     1

x     0     0     y     1

x     0     0     y     0

0     0     0     0     0

x     0     1     y     0

Заменяя каждый вариант на соответствующую букву, получим таблицу

Т                 Ы                У    Т                 Ц

Р     Е     Л     Е     Г     Р     А    Ж

В                 Щ               С     В                 Ф

Выбирая по одной букве в каждом столбце таблицы, находим «читаемое» слово ТЕЛЕГРАФ.

Перепутанные проводки

Для передачи сообщений по телеграфу каждая буква русского алфавита (буквы Е и Ё отождествлены) представляется в виде пятизначной комбинации из нулей и единиц, соответствующих двоичной записи номера данной буквы в алфавите (нумерация букв начинается с нуля). Например, буква А представляется в виде 00000, буква Б - 00001, буква Ч - 10111, буква Я - 11111. Передача пятизначной комбинации производится по кабелю, содержащему пять проводов. Каждый двоичный разряд передается по отдельному проводу. При приеме сообщения Криптоша перепутал провода, поэтому вместо переданного слова получен набор букв ЭАВЩОЩИ. Найдите переданное слово.

Решение: Заметим, что после перепутывания проводков внутри каждой пятизначной комбинации число единиц не изменилось. Подпишем под каждой буквой полученного сообщения те буквы, которые представляются пятизначной комбинацией с тем же числом единиц:

Э     А    В     Щ   О    Щ   И

Ю               Б     З     З     З     Б

Ы                Д     Л     Л     Л     В

Ч            И    Н    Н    Н    Д

П                Р     О    У    О    Р

У    Х    У        

Х    Ц    Х        

Ц    Щ   Ц        

Ъ    Ъ    Ъ        

Ь     Ь     Ь         

Выбирая по одной букве в каждом столбце таблицы, находим единственное «читаемое» слово ПАРОХОД.

 

 

Крокодил Гена и Чебурашка

Крокодил Гена посылает Чебурашке по радиоканалу сообщение, заменяя его

буквы наборами из нулей и единиц согласно табл.1 (другие буквы не встретились).

 

Из-за помех некоторые биты исказились, но не более двух в одном наборе.

Определите, какое сообщение отправил крокодил Гена, если Чебурашка получил:

Решение:

По условию задачи в каждом наборе искажено не более двух бит. Заметим, что наборы из табл. 1, соответствующие различным буквам, отличаются по крайней мере в трех позициях. Отсюда следует, что искажение одного или двух битов в любом наборе из табл. 1, не делает его другим набором из табл. 1 (на это потребовалось бы по крайней мере три искажения). Значит все те наборы из письма Гены, которые соответствуют наборам из табл. 1, просто не были искажены. Выпишем, соответствующие им буквы:                                     УД*Р*А*Т*Р**Т*И*Т*С*Ч*Д*У*ИХ*Д*Р**

(“*” отмечены пока не известные буквы). Итак, уже имеется некоторая основа сообщения, которая поможет нам подобрать остальные буквы. Для восстановления третьей буквы требуется посмотреть, какие наборы из табл. 1 могли при искажении одного/двух битов стать набором (0,0,1,0,0,0,0), и выбрать тот набор, которому соответствует буква, подходящая по смыслу. Так, набор (0,0,1,0,0,0,0) мог быть получен из набора (0,0,0,0,0,0,0) (при искажении третьего бита) или из набора (1,0,1,0,0,1,0) (при искажении первого и седьмого битов) или из набора (0,0,1,1,0,0,1) (при искажении четвертого и седьмого битов). Очевидно, что по смыслу подходит только набор (0,0,0,0,0,0,0), соответствующий букве А. Аналогичным образом восстанавливаются остальные неизвестные буквы. В результате, получаем письмо Гены.

УДАР МАСТЕРА СТОИТ ТЫСЯЧИ ДРУГИХ УДАРОВ.

Экспоненциальное гаммирование

Для зашифрования сообщения на русском языке, записанного без знаков препинания и пробелов, используется последовательность натуральных чисел x1, x2,..., удовлетворяющая соотношению: xk = b·8a(k-1), k = 1, 2,... Здесь a и b - фиксированные (но неизвестные) натуральные числа. Зашифрование производится следующим образом. Первую букву сообщения заменяют числом согласно таблице 1 и складывают с x1. Потом также заменяют вторую букву и складывают с x2 и т.д.

Затем все полученные суммы заменяют остатками от деления на 31, а остатки заменяют буквами согласно таблице 2.

В результате получился текст: