

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Теорема 1 (критерий возрастания дифференцируемой на интервале функции) Для того, чтобы дифференцируемая на интервале  функция
функция  была возрастающей на этом интервале, необходимо и достаточно, чтобы
была возрастающей на этом интервале, необходимо и достаточно, чтобы 
 .
.
Теорема 2 (критерий убывания дифференцируемой на интервале функции) Для того, чтобы дифференцируемая на интервале  функция
функция  была убывающей на этом интервале, необходимо и достаточно, чтобы
была убывающей на этом интервале, необходимо и достаточно, чтобы 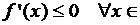
 .
.
Теорема 3 (достаточное условие строгого возрастания (убывания) функции) Если 

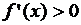 , то
, то  строго возрастает на интервале
строго возрастает на интервале  . Если
. Если 

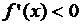 , то
, то  строго убывает на интервале
строго убывает на интервале  .
.
Теорема 4 Если  непрерывна на отрезке
непрерывна на отрезке  , дифферен-цируема на интервале
, дифферен-цируема на интервале  и
и 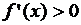 для
для 
 , то
, то  строго возрастает на
строго возрастает на  .
.
Экстремумы функции
О. Точки, в которых  , называются стационарными.
, называются стационарными.
О. Точки, в которых  непрерывна, а
непрерывна, а  или не существует, называются критическими
или не существует, называются критическими
Из теоремы Ферма следует, что если 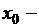 точка экстремума, то
точка экстремума, то 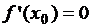 . Поэтому точки экстремума следует искать среди критических точек.
. Поэтому точки экстремума следует искать среди критических точек.
Однако не всякая критическая точка является точкой экстремума. Например, для  , но
, но  не является точкой экстремума.
не является точкой экстремума.
Теорема (I достаточное условие строгого экстремума) Пусть  дифференцируема в некоторой
дифференцируема в некоторой  и непрерывна в точке
и непрерывна в точке  . Тогда 1) если
. Тогда 1) если 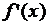 меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку  , т.е.
, т.е. 

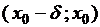
 , а
, а 
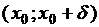
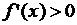 , то
, то  – точка строгого локального минимума функции
– точка строгого локального минимума функции  ;
;
2) если 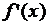 меняет знак с плюса на минус при переходе через точку
меняет знак с плюса на минус при переходе через точку  , то
, то  – точка строгого локального максимума функции
– точка строгого локального максимума функции  .
.
Наибольшее и наименьшее значения функции на отрезке
По теореме Вейерштрасса, если  непрерывна на отрезке
непрерывна на отрезке  , то на этом отрезке существуют такие точки, в которых
, то на этом отрезке существуют такие точки, в которых  достигает свои максимальное и минимальное значения. Если
достигает свои максимальное и минимальное значения. Если  имеет в точках
имеет в точках  локальные экстремумы, то её максимальное и минимальное значения находятся среди чисел
локальные экстремумы, то её максимальное и минимальное значения находятся среди чисел 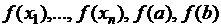 .
.
|
|
Выпуклость функции
О. Функция  называется выпуклой вверх на отрезке
называется выпуклой вверх на отрезке  , если
, если 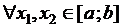 выполняется неравенство:
выполняется неравенство:  .
.
То есть для любых двух точек 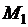 и
и 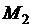 графика функции
графика функции  середина хорды
середина хорды 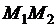 лежит ниже соответствующей точки графика.
лежит ниже соответствующей точки графика.
О. Функция  называется выпуклой вниз на отрезке
называется выпуклой вниз на отрезке  , если
, если 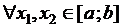 выполняется неравенство:
выполняется неравенство: 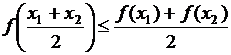 .
.
Теорема (достаточное условие выпуклости) Пусть 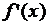 существует на отрезке
существует на отрезке  , а
, а 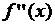 – на интервале
– на интервале  . Тогда
. Тогда
а) если 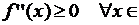
 , то
, то  выпукла вниз на отрезке
выпукла вниз на отрезке  ; б) если
; б) если 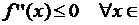
 , то
, то  выпукла вверх на отрезке
выпукла вверх на отрезке  .
.
Замечание. а) если 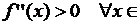
 , то
, то  строго выпукла вниз на отрезке
строго выпукла вниз на отрезке  ; б) если
; б) если 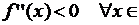
 , то
, то  строго выпукла вверх на
строго выпукла вверх на  .
.
Точки перегиба
О. Пусть  непрерывна в точке
непрерывна в точке  и имеет в этой точке конечную или бесконечную производную. Тогда если
и имеет в этой точке конечную или бесконечную производную. Тогда если  при переходе через точку
при переходе через точку  меняет направление выпуклости, т.е.
меняет направление выпуклости, т.е. 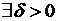 такое, что на одном из интервалов
такое, что на одном из интервалов 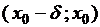 ,
, 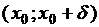 она выпукла вверх, а на другом выпукла вниз, то
она выпукла вверх, а на другом выпукла вниз, то  называется точкой перегиба функции
называется точкой перегиба функции  .
.
Например, для  – точка перегиба.
– точка перегиба.
Теорема (необходимое условие точки перегиба) Если 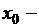 точка перегиба функции
точка перегиба функции  и
и 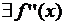 в некоторой окрестности
в некоторой окрестности 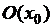 , непрерывная в точке
, непрерывная в точке  , то
, то 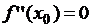 .
.
Теорема (достаточное условие точки перегиба) Если  непрерывна в точке
непрерывна в точке  , имеет
, имеет 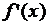 в точке
в точке  и при переходе через точку
и при переходе через точку 
 меняет знак, то
меняет знак, то  – точка перегиба функции
– точка перегиба функции  .
.
Асимптоты
О. Если  или
или 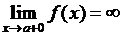 , то прямая
, то прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  .
.
Например, для функций  прямая
прямая 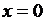 –вертикальная асимптота, для функции
–вертикальная асимптота, для функции  прямые
прямые  являются вертикальными асимптотами.
являются вертикальными асимптотами.
Вертикальные асимптоты следует искать в точках разрыва функции  или в граничных точках области определения.
или в граничных точках области определения.
О. Прямая  называется асимптотой графика функции
называется асимптотой графика функции  при
при 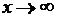 , если
, если 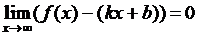 .
.
Если  , то асимптота называется наклонной.
, то асимптота называется наклонной.
Если 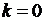 , то асимптота
, то асимптота  называется горизонтальной.
называется горизонтальной.
Например, для функций  прямая
прямая 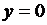 –горизонтальная асимптота, для функции
–горизонтальная асимптота, для функции  прямые
прямые 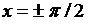 являются горизонтальными асимптотами.
являются горизонтальными асимптотами.
|
|
Теорема Прямая  является асимптотой графика функции
является асимптотой графика функции  при
при 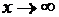 тогда, и только тогда, когда существуют и конечны оба предела:
тогда, и только тогда, когда существуют и конечны оба предела: 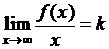 и
и  .
.
Схема исследования функции
1) Найти область определения функции 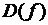 . Выяснить, является ли функция четной, нечетной, периодической.
. Выяснить, является ли функция четной, нечетной, периодической.
2) Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства (т.е. промежутки, на которых 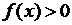 и
и 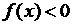 ).
).
3) Найти асимптоты графика функции. Найти односторонние пределы в точках разрыва и граничных точках области определения.
4) Вычислить производную функции. Найти промежутки возрастания и убывания, экстремумы функции.
5) Вычислить вторую производную функции. Найти промежутки выпуклости вверх и вниз, точки перегиба.
6) Изобразить график функции.
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!