


Формула Ньютона-Лейбница


Основные свойства определенного интеграла





Простейшие оценки опр.интеграла. Теорема о среднем.
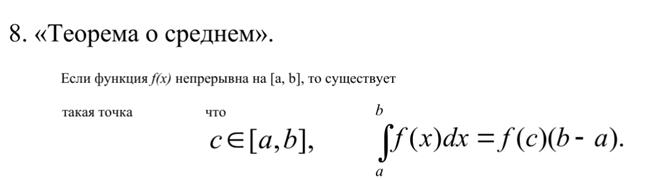
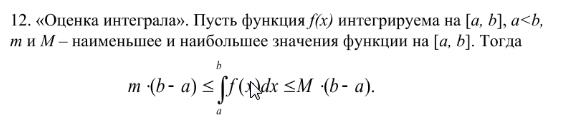

52. Замена переменной под знаком определенного интеграл

Интегрирование четных и нечетных функций по промежутку, симметричному относительно нуля

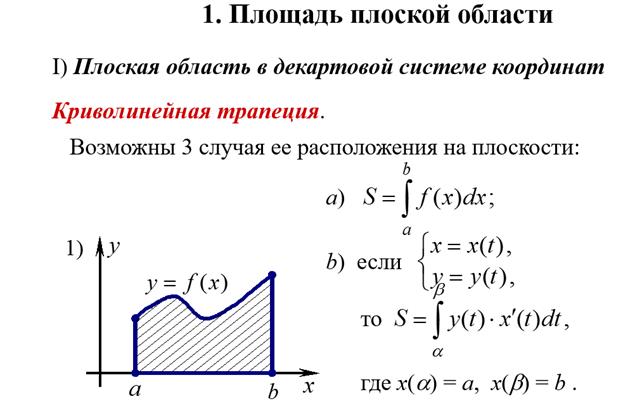
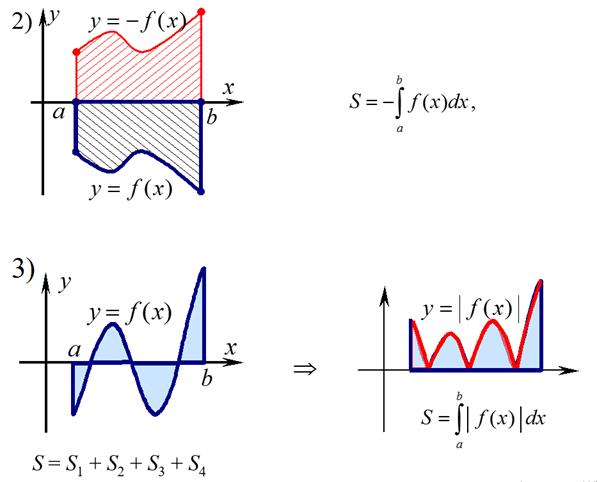
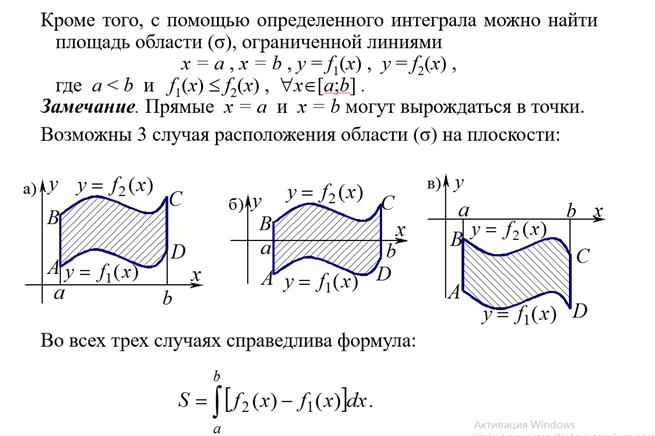
54. Вычисление площади плоских фигур в прямоугольной системе координат и в случае параметрического задания граничного контура
Вычисление объема пространственного тела по заданным площадям его сечений
Пусть V – замкнутая и ограниченная область в Oxyz (тело).
Пусть S (x) (a £ x £ b) – площадь любого сечения тела плоскостью, перпендикулярной оси Ox.
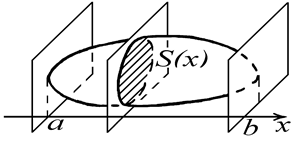
Найдём объем тела V.
1) Разобьем [ a; b ] на n частей точками
x 0 = a, x 1, x 2, …, xn = b (где x 0 < x 1 < x 2 < … < xn)
Плоскости x = x 0, x = x 1, x = x 2, …, x = xn разобьют (V) на части
(V 1), (V 2), …, (Vn) Þ V = ∑ Vi, где Vi – объем (Vi).
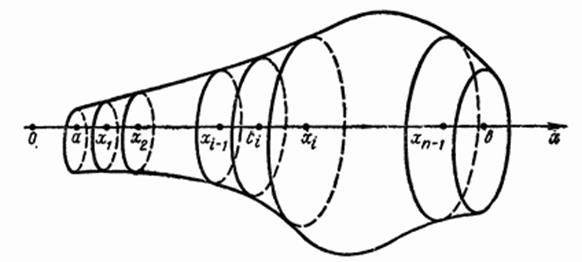
Вычисление объема тела вращения



Определение длины дуги и ее вычисление в прямоугольной системе координат



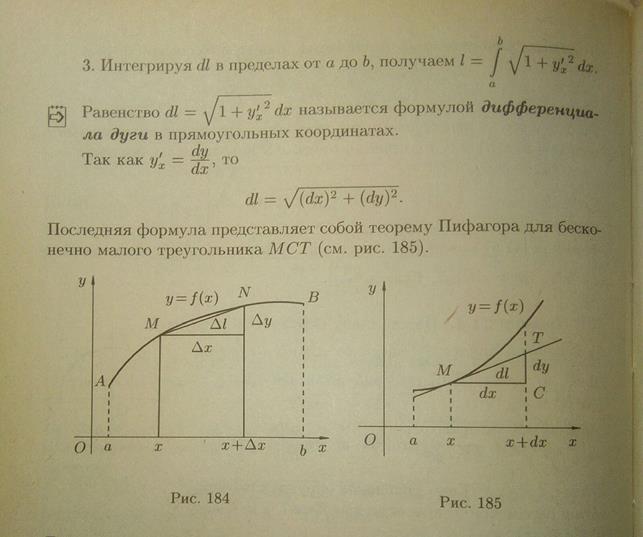
58) Определение длины дуги и ее вычисление в случае параметрического задания кривой
Рассмотрим теперь случай, когда кривая, длину которой необходимо вычислить, задана параметрически, то есть  при этом изменение
при этом изменение 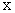 от
от  до
до  приводит к изменению
приводит к изменению  от
от  до
до  . Пусть функции
. Пусть функции 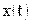 и
и 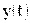 непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке 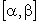 и при этом
и при этом 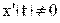 . Тогда
. Тогда  , а
, а  . Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
. Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
 .
.
В случае пространственной кривой ее параметрическое задание будет выглядеть следующим образом:

Если указанные функции непрерывны вместе со своими производными на отрезке 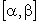 , то можно доказать, что длина данной кривой вычисляется по формуле
, то можно доказать, что длина данной кривой вычисляется по формуле
 .
.
Несобственные интегралы 1 рода
Для существования определенного интеграла необходимы условия:
1) [a;b] – конечен,
2) f(x) – ограничена (необходимое условие существования определенного интеграла).
Несобственные интегралы – обобщение понятия определенного интеграла на случай когда одно из этих условий не выполнено.Несобственные интегралы бывают двух видов.Несобственный интеграл 1 рода возникает, когда по крайней мере одно из чисел a, b бесконечно. 



Несобственные интегралы 2 рода
Если подинтегральная функция имеет на (конечном) интервале интегрирования разрыв второго рода, говорят о несобственном интеграле второго рода.
Определение и основные свойства
Обозначим интервал интегрирования [ a, b ], оба этих числа ниже полагаются конечными. Если имеется всего 1 разрыв, он может находиться или в точке a, или в точке b, или внутри интервала (a, b). Рассмотрим сначала случай, когда разрыв второго рода имеется в точке a, а в остальных точках подинтегральная функция непрерывна. Итак, мы обсуждаем интеграл
















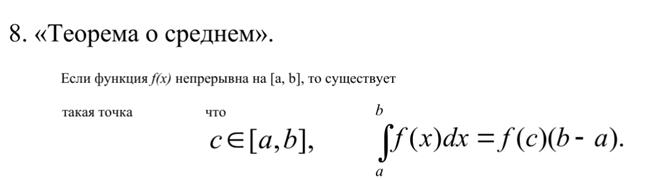
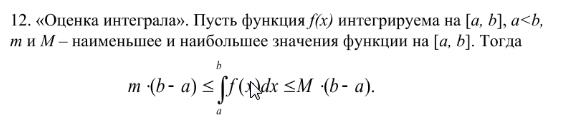















 при этом изменение
при этом изменение 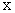 от
от  до
до  приводит к изменению
приводит к изменению  от
от  до
до  . Пусть функции
. Пусть функции 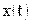 и
и 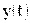 непрерывны вместе со своими производными на отрезке
непрерывны вместе со своими производными на отрезке 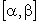 и при этом
и при этом 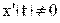 . Тогда
. Тогда  , а
, а  . Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
. Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5): .
.
 .
.








