Сопряженные элементы и классы.

Матрицы.

Обратная - это матрица, которая при умножении на данную дает единичную. Т.е. . Матрица, у которой детерминант равен нулю, называется сингулярной и не имеет обратной. Неквадратные матрицы не имеют обратных, т.к. их детерминант не определен.

Комплексно-сопряженная 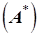 - знак мнимой части каждого элемента заменен на обратный. Если  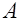- действительная, то .

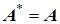Транспонированная 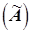 - строки заменяются на столбцы.

Симметричная.

Кососимметричная.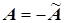

Эрмитово-сопряженная 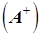; одновременно применяются операции комплексного сопряжения и транспонирования.

Если 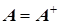  - матрица просто эрмитова.

Свойства матриц.

, , .

Прямое произведение матриц.

.

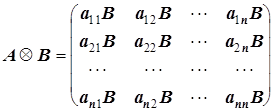Унитарная матрица.

Если 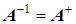 , то матрица  - унитарная ее детерминант равен  1.

Унитарное преобразование матрицы : .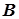

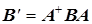Вращение вектора можно представить как произведение матриц 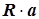, где 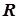 - матрица преобразования координат;  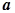- вектор-столбец исходных значений координат. В двухмерном случае поворот на угол Q задается матрицей:

                .

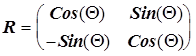Эта матрица определяет поворот вектора на угол Q по часовой стрелке или поворот системы координат против часовой стрелки. (Угол Q - положительный.)

Поворот, обратный данному, есть поворот на угол (-Q). Т.о. матрица

                 .

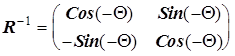Учитывая, что 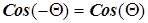 и 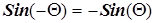 получим

                  .

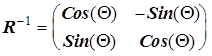Т.о. 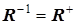 , следовательно матрица  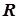- унитарная.

В трех измерениях матрица поворота имеет вид:

                           .

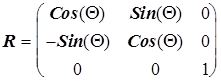Третье измерение - ось поворота.

 

Операции симметрии.

Рассмотрим множество операций симметрии, используемых при описании молекул. Операция симметрии - действие при применении которого конфигурация объекта совпадает с первоначальной. Операция симметрии должна быть определена по отношению к элементу симметрии. Элемент симметрии - это геометрический объект, такой, как плоскость, линия, точка, относительно которого выполняет операция симметрии.

Существует пять различных типов элементов симметрии, которыми может обладать изолированный объект.

* Тождественная (или единичная) операция. Эта операция либо ничего не делает с системой, либо возвращает ее в исходное состояние (поворот на 360^о).

* Ось вращения. Если поворот на угол 2 p /n приводит к конфигурации совпадающей с исходной, то он называется поворотом типа C_n. Поворот осуществляется по часовой стрелке. Соответствующий элемент симметрии C_n - собственная ось поворота n -го порядка. Поворот на угол, кратный некоторому элементарному углу (т.е. на угол m2 p /n), обозначается как C_n^m. Если кратный поворот можно выразить через поворот более низкого порядка, то используется обозначение поворота низкого порядка. Многие системы обладают несколькими собственными осями симметрии. В этом случае ось наивысшего порядка называется главной осью. Если имеется несколько осей одного и того же порядка, то одну из них произвольно выбирают главной.

* Плоскость симметрии. Обозначение - s. Плоскости симметрии в зависимости от их связи с главной и вспомогательной осями разделяются на три типа. Существуют: вертикальная плоскость симметрии s _v , содержащая главную ось; диэдральная плоскость симметрии s _d , которая содержит главную ось и делит угол пополам между вспомогательными осями 2-го порядка, перпендикулярными к главной оси, или иногда содержит другие элементы; горизонтальная плоскость симметрии s _h  , перпендикулярная главной оси.

* Несобственная ось поворота или зеркально-поворотная ось n -го порядка. Обозначается как S_n. Представляет собой поворот относительно C_n с последующим отражением в горизонтальной плоскости s _h  , перпендикулярной этой оси. Элементы симметрии C_n и s _h  могут в отдельности не существовать.

* Точка инверсии (i). При отражении в этой точке любая точка пространства с координатами (x,y,z) переходит в точку с координатами (-x,-y,-z).

 

 

Лекция 2.

Рассмотрим операции симметрии на примере молекулы аммиака NH₃. Геометрическое строение этой молекулы - тригональная пирамида, в основании которой лежат атомы водорода, образующие правильный треугольник. [Нарисовать структуру и пронумеровать атомы водорода как показано на рис. 1]. При операциях симметрии происходит взаимозамещение атомов водорода; атома азота остается неподвижным. Поэтому для иллюстрации операций симметрии рассмотрим только атомы водорода и для этого их пронумеруем (рис.1). [Далее подробно рассмотреть действие операций симметрии E, C₃, C₃ ² , s_v , s_v¢ , s_v² в соответствии с рис. 2]. Оси поворота проходят по оси z, плоскости включают ось поворота и один из атомов водорода (см. рис. 2). Поворот - по часовой стрелке.

Используя рис. 2 можно легко определить результат последовательного выполнения (или произведения)двух операций симметрии. При этом расположение элементов симметрии (т.е. осей поворота и плоскостей) в декартовом пространстве остается неизменным. В итоге для рассматриваемого примера можно составить таблицу произведений операций симметрии (см. ниже).

Таблица 1. Произведения операций симметрии.

	E	C3	C3 2	sv	sv¢	sv²
E	E	C3	C3 2	sv	sv¢	sv²
C3	C3	C3 2	E	sv¢	sv²	sv
C3 2	C3 2	E	C3	sv²	sv	sv¢
sv	sv	sv²	sv¢	E	C3 2	C3
sv¢	sv¢	sv	sv²	C3	E	C3 2
sv²	sv²	sv¢	sv	C3 2	C3	E

Каждый элемент таблицы - результат последовательного выполнения 2-х операций симметрии. Первой выполняется операция соответствующая столбцу, второй - строке.

[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно. На примере таблицы показать, что операции симметрии молекулы NH₃ удовлетворяют групповым теоремам.]

Групповые теоремы:

1. Произведение 2-х элементов дает третий элемент, также являющийся элементом группы.

2. Выполняется ассоциативный закон. Т.е. (ab)c=a(bc). Рассмотрим тройное произведение C₃s_vC₃ ²      :

 (C₃s_v)C₃ ²             = s_v¢    C₃ ²         = s_v²   

 C₃(s_vC₃ ²     )  = C₃ s_v¢     = s_v².  

3. В группе есть элемент, коммутирующий с любым другим элементом и оставляющим его неизменным. Это единичный элемент. EA=AE=E.

4. Элемент, обратный к каждому элементу группы, также является элементом группы. Например: C₃ C₃ ²           = C₃ ² C₃. Отражения в плоскости обратны сами себе.

 

Таким образом операции симметрии NH₃ удовлетворяют групповым постулатам и составляют математическую группу. Аналогичная ситуация имеет место и для любых других систем. Группы, описывающие симметрию ядер молекулы, называются точечными, т.к. все элементы симметрии пересекаются, по крайней мере, в одной точке.

 

Генераторы и подгруппы.

В приведенном выше примере, рассмотрим два элемента C₃ и s_v и найдем результаты произведения их друг с другом и самих на себя (см. табл. 1):

C₃s_v = s_v¢        ;                s_v C₃ = s_v²; C₃ C₃ = C₃ ²       ; s_v s_v = Е.

Т.о. получены все элементы группы. Эти элементы называются генераторами группы. Полное число элементов в группе - порядок группы (в нашем примере порядок равен 6). В рассматриваемом примере операции C₃ и s_v не единственный набор генераторов. Это могут быть и пары (C₃, s_v¢   ), (C₃, s_v²         ), (C₃ ²  , s_v), (C₃ ² , s_v¢   ) и (C₃ ² , s_v²         ). Однако обязательно должна быть одна из осей C₃ или C₃ ²       и одна из плоскостей s_v, s_v¢     или s_v²         . Поэтому эту группы и обозначают как C_3v. Элементы C₃ и C₃ ²   не порождают всю группу. Но они вместе с элементом Е порождают подгруппу точечной группы C_3v. Подгруппа - множество элементов, удовлетворяющее групповым постулатам. [ Показать с использованием табл. 1, что элементы {Е, C₃ и C₃ ²  }составляют группу C₃.] Кроме того, в группе C_3v можно выделить еще три подгруппы {E, s_v}, {E, s_v¢    }и {E, s_v²          }полностью эквивалентные друг другу. Эти подгруппы называются циклическими, т.е. содержат степени одного и того же элемента. Единичный элемент в циклической группе также является степенью указанного элемента.

 

Произведения групп.

Одной из операций, которые могут быть определены для групп, является произведение независимых групп. Если группа А состоит из n элементов, а B из m элементов, то их произведение содержит n´m элементов вида A_iB_j. Например, произведением групп {Е, C₃ и C₃ ²  }и {E, s_v}является:

{Е, C₃, C₃ ²  }´{E, s_v}= (Е, C₃, C₃ ²  , s_v,s_v¢   , s_v²         ) [ рассмотреть подробнее]

Т.о. группа C_3v порождена произведением своих двух независимых подгрупп. В то же время подгруппы {E, s_v}и {E, s_v¢    } не порождают группы:

{E, s_v}´{E, s_v¢    }= (Е, s_v, s_v¢   , C₃ ²         ).

Если мы умножим {E, s_v}´{Е, C₃, C₃ ²  }= (Е, C₃, C₃ ²  , s_v, s_v²          ,s_v¢   ) то получим те же элементы, что и выше, но в другом порядке. Т.к. C₃ и C₃ ²                       не коммутируют с s_v. Произведения групп с некоммутирующими элементами называют полупрямыми (обозначают символом ^). Произведения с коммутирующими элементами называют прямыми (символом ´). Таким образом, если обозначим группу {E, s_v}как C_s, то можно записать, что C_3v = C₃^ C_s .

 

Лекция 3.

Отображения, морфизмы.

 

Часто бывает полезно представить элементы некоторой группы другими величинами, удовлетворяющими той же таблице произведений, что и заданная группа. Это означает, что данная группа отображается в новую группу, причем каждый элемент в первоначальной группе имеет образ в новой. При этом совсем не обязательно, чтобы различные элементы в первоначальной группе имеют различные образы в новой. Если различные элементы одной группы имеют различные образы в другой группе, то эти группы называются изоморфными. В противном случае - гомоморфными. В качестве примера рассмотрим отображения группы C₄:

C4	E	C4	C2	C42
	1	1	1	1
	1	-1	1	-1
	1	i	-1	-i
	1	-i	-1	i

 

Если в качестве группового произведения принять обычное умножение, то элементы каждого из 4-х отображений образуют группу. Первая группа имеет порядок 1, вторая - 2, две последние - 4. В первом случае 4 элемента первой группы отображаются в один, во втором два в один. Т.о. первые два - гомоморфизмы. В двух последних различным элементам первоначальной группы соответствуют различные образы в отображениях. Т.о. эти группы изоморфны.

Рассмотрим вновь молекулу NH₃ и каждому элементу симметрии поставим в соответствие матрицу преобразования декартовых координат атомов.

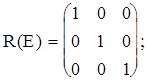
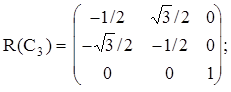
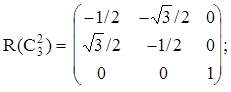
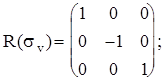
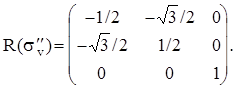
Матрицы, соответствующие операциям s_v¢ и s_v²     , можно получить из произведения матриц R(C₃ ² )R(s_v) и R(C₃)R(s_v), соответственно, или через матрицу генератора s_d при (p/n)=120^o и (p/n)=-120^o.

Из произведений матриц можно составить таблицу полностью идентичную таблице произведений элементов точечной группы C_3v. Т.о. этот набор матриц образует группу изоморфную точечной группе C_3v. Если существует множество матриц, представляющих собой группу и имеющих такую же таблицу произведений что и данная группа, то говорят, что эти матрицы порождают матричное представление (или просто представление) группы. Группа матриц, являющаяся представлением данной группы, не обязательно должна быть изоморфна последней. Матрицы могут быть одномерными, двумерными, трехмерными и т.д. Они могут быть действительными, комплексными и мнимыми. Единственное требование - они должны быть гомоморфны рассматриваемой группе и удовлетворять таблице произведений группы. Может существовать бесконечное множество возможных представлений. В том случае, если группа матриц изоморфна точечной группе, то они образуют точное представление группы.

Однако подробное и полное изложение теории представлений является предметом отдельного специального курса. Здесь речь пойдет лишь о тех понятиях теории представлений, которые будут необходимы для практического применения теории групп. Одной из основных задач, возникающих при поиске представлений групп, является определение так называемых неприводимые представлений. Неприводимые представления - матричные представления самой низшей размерности, которые нельзя преобразовать друг в друга. Неприводимые представления обладают следующими свойствами.

Если неприводимые представления одномерны, то они сами образуют группу.

Сумма квадратов размерностей неприводимых представлений равна порядку группы.

Число различных неприводимых представлений группы равно числу ее классов.

Рассмотрим группу C₂ {E, C₂}. Матрицы соответствующие операциям симметрии имеют вид:

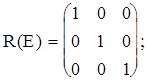
Эти матрицы образуют представление группы C₂. Однако оно не является самым простым. Поскольку матрицы диагональны, то x, y и z координаты преобразуются независимо друг от друга. Рассматривая только эти компоненты получим три независимых отображения группы C₂:

	E	C2
G(x)	1	-1
G(y)	1	-1
G(z)	1	1

 

Т.к. базисные вектора декартовой системы взаимноортогональны, то эти отображения взаимонезависимы. В отдельности - это неприводимые представления группы C₂. Числа, выражающие эти представления, называются характерами. Характер - след матрицы, соответствующей данной операции симметрии. Здесь представления G(x) и G(y) совпадают и, следовательно, у группы C₂ есть только два одномерных неприводимых представления. Таблица характеров неприводимых представлений для группы C₂ имеет вид:

С2	E	C2
A	1	1
B	1	-1

Таблица характеров включает в себя характеры для различных операций в каждом неприводимом представлении.

Рассмотрим группу C₃ {E, 2C₃}. Матрицы соответствующие операциям симметрии имеют вид:

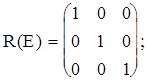
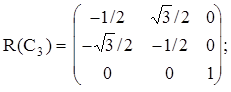
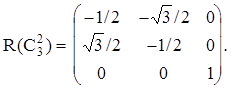
Матрицы, соответствующие операциям поворота, недиагональны. Т.о. x и y компоненты взаимозависимы. Следовательно из нельзя использовать отдельно для построения представлений. Однако z-компонента порождает независимое представление. Еще одно представление дают квадратные матрицы 2-го порядка, описывающие взаимное преобразование координат x и y. Это будет также неприводимое представление. Таблицу характеров можно записать двумя способами. Первый - через следы матриц:

С3	E	2C3
A	1	1
E	2	-1

Второй способ - диагонализация матриц. В результате приведения матриц, описывающих повороты, к диагональному виду получим новые матрицы:

     

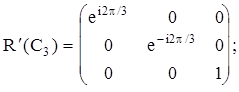
Два первых диагональных элемента являются комплексносопряженными. Двумерное представление можно разложить на два мнимых одномерных и таблицу характеров записать в виде:

С3	E	C3	C3 2
A	1	1	1
E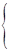

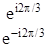
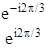
Порядок группы - 3. Размерности представлений 1² + 1² + 1² = 3. Для циклических групп рассматриваются мнимые представления.

Группа C_2v {E, C₂, s_v^{x     z}, s_v^{y  z}}. Матрицы операций симметрии:

                        

               

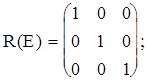
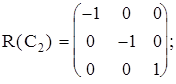
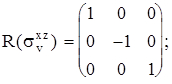
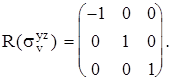
Матрицы диагональны, т. о. получим таблицу представлений:

	E	C2	svx     z	svy  z
G(x)	1	-1	1	-1
G(y)	1	-1	-1	1
G(z)	1	1	1	1

Однако в соответствии со свойствами представлений должно быть 4 неприводимых представления. Четвертое находится на основании свойства: G(a)´ G(b)= G(c) [a_i´b_i=c_i]. Т.о.

G(z)´ G(x)={1 -1 1 -1 }=G(x)

G(z)´ G(y)={1 -1 -1 1 }=G(y)

 G(x)´ G(y)={1 1 -1 -1 } ® новое представление.

В результате таблица характеров для группы C_2v примет вид:

	E	C2	svx     z	svy  z
A1	1	1	1	1
A2	1	1	-1	-1
B1	1	-1	1	-1
B2	1	-1	-1	1

В итоге мы имеем:

группа C₂ - 2 представления - 2 вектора в двухмерном пространстве;

группа C₃ - 1 одномерное и 1 двухмерное представления - 3 вектора в

                  трехмерном пространстве;

группа C_2v - 4 одномерных представления - 4 вектора в четырехмерном

                  пространстве.

Т.о. неприводимые представления описывают элементы симметрии в n -мерном пространстве, построенном на системе n независимых базисных векторов.

 

Лекции 5-6.

Матрицы.

Обратная - это матрица, которая при умножении на данную дает единичную. Т.е. . Матрица, у которой детерминант равен нулю, называется сингулярной и не имеет обратной. Неквадратные матрицы не имеют обратных, т.к. их детерминант не определен.

Комплексно-сопряженная 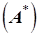 - знак мнимой части каждого элемента заменен на обратный. Если  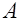- действительная, то .

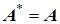Транспонированная 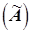 - строки заменяются на столбцы.

Симметричная.

Кососимметричная.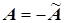

Эрмитово-сопряженная 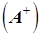; одновременно применяются операции комплексного сопряжения и транспонирования.

Если 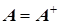  - матрица просто эрмитова.

Свойства матриц.

, , .

Прямое произведение матриц.

.

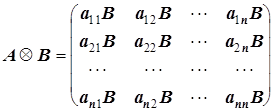Унитарная матрица.

Если 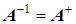 , то матрица  - унитарная ее детерминант равен  1.

Унитарное преобразование матрицы : .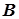

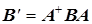Вращение вектора можно представить как произведение матриц 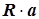, где 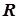 - матрица преобразования координат;  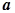- вектор-столбец исходных значений координат. В двухмерном случае поворот на угол Q задается матрицей:

                .

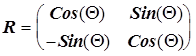Эта матрица определяет поворот вектора на угол Q по часовой стрелке или поворот системы координат против часовой стрелки. (Угол Q - положительный.)

Поворот, обратный данному, есть поворот на угол (-Q). Т.о. матрица

                 .

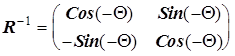Учитывая, что 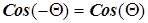 и 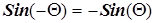 получим

                  .

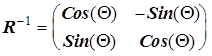Т.о. 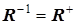 , следовательно матрица  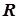- унитарная.

В трех измерениях матрица поворота имеет вид:

                           .

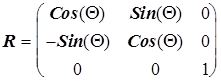Третье измерение - ось поворота.

 

Операции симметрии.

Рассмотрим множество операций симметрии, используемых при описании молекул. Операция симметрии - действие при применении которого конфигурация объекта совпадает с первоначальной. Операция симметрии должна быть определена по отношению к элементу симметрии. Элемент симметрии - это геометрический объект, такой, как плоскость, линия, точка, относительно которого выполняет операция симметрии.

Существует пять различных типов элементов симметрии, которыми может обладать изолированный объект.

* Тождественная (или единичная) операция. Эта операция либо ничего не делает с системой, либо возвращает ее в исходное состояние (поворот на 360^о).

* Ось вращения. Если поворот на угол 2 p /n приводит к конфигурации совпадающей с исходной, то он называется поворотом типа C_n. Поворот осуществляется по часовой стрелке. Соответствующий элемент симметрии C_n - собственная ось поворота n -го порядка. Поворот на угол, кратный некоторому элементарному углу (т.е. на угол m2 p /n), обозначается как C_n^m. Если кратный поворот можно выразить через поворот более низкого порядка, то используется обозначение поворота низкого порядка. Многие системы обладают несколькими собственными осями симметрии. В этом случае ось наивысшего порядка называется главной осью. Если имеется несколько осей одного и того же порядка, то одну из них произвольно выбирают главной.

* Плоскость симметрии. Обозначение - s. Плоскости симметрии в зависимости от их связи с главной и вспомогательной осями разделяются на три типа. Существуют: вертикальная плоскость симметрии s _v , содержащая главную ось; диэдральная плоскость симметрии s _d , которая содержит главную ось и делит угол пополам между вспомогательными осями 2-го порядка, перпендикулярными к главной оси, или иногда содержит другие элементы; горизонтальная плоскость симметрии s _h  , перпендикулярная главной оси.

* Несобственная ось поворота или зеркально-поворотная ось n -го порядка. Обозначается как S_n. Представляет собой поворот относительно C_n с последующим отражением в горизонтальной плоскости s _h  , перпендикулярной этой оси. Элементы симметрии C_n и s _h  могут в отдельности не существовать.

* Точка инверсии (i). При отражении в этой точке любая точка пространства с координатами (x,y,z) переходит в точку с координатами (-x,-y,-z).

 

 

Лекция 2.

Рассмотрим операции симметрии на примере молекулы аммиака NH₃. Геометрическое строение этой молекулы - тригональная пирамида, в основании которой лежат атомы водорода, образующие правильный треугольник. [Нарисовать структуру и пронумеровать атомы водорода как показано на рис. 1]. При операциях симметрии происходит взаимозамещение атомов водорода; атома азота остается неподвижным. Поэтому для иллюстрации операций симметрии рассмотрим только атомы водорода и для этого их пронумеруем (рис.1). [Далее подробно рассмотреть действие операций симметрии E, C₃, C₃ ² , s_v , s_v¢ , s_v² в соответствии с рис. 2]. Оси поворота проходят по оси z, плоскости включают ось поворота и один из атомов водорода (см. рис. 2). Поворот - по часовой стрелке.

Используя рис. 2 можно легко определить результат последовательного выполнения (или произведения)двух операций симметрии. При этом расположение элементов симметрии (т.е. осей поворота и плоскостей) в декартовом пространстве остается неизменным. В итоге для рассматриваемого примера можно составить таблицу произведений операций симметрии (см. ниже).

Таблица 1. Произведения операций симметрии.

	E	C3	C3 2	sv	sv¢	sv²
E	E	C3	C3 2	sv	sv¢	sv²
C3	C3	C3 2	E	sv¢	sv²	sv
C3 2	C3 2	E	C3	sv²	sv	sv¢
sv	sv	sv²	sv¢	E	C3 2	C3
sv¢	sv¢	sv	sv²	C3	E	C3 2
sv²	sv²	sv¢	sv	C3 2	C3	E

Каждый элемент таблицы - результат последовательного выполнения 2-х операций симметрии. Первой выполняется операция соответствующая столбцу, второй - строке.

[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно. На примере таблицы показать, что операции симметрии молекулы NH₃ удовлетворяют групповым теоремам.]

Групповые теоремы:

1. Произведение 2-х элементов дает третий элемент, также являющийся элементом группы.

2. Выполняется ассоциативный закон. Т.е. (ab)c=a(bc). Рассмотрим тройное произведение C₃s_vC₃ ²      :

 (C₃s_v)C₃ ²             = s_v¢    C₃ ²         = s_v²   

 C₃(s_vC₃ ²     )  = C₃ s_v¢     = s_v².  

3. В группе есть элемент, коммутирующий с любым другим элементом и оставляющим его неизменным. Это единичный элемент. EA=AE=E.

4. Элемент, обратный к каждому элементу группы, также является элементом группы. Например: C₃ C₃ ²           = C₃ ² C₃. Отражения в плоскости обратны сами себе.

 

Таким образом операции симметрии NH₃ удовлетворяют групповым постулатам и составляют математическую группу. Аналогичная ситуация имеет место и для любых других систем. Группы, описывающие симметрию ядер молекулы, называются точечными, т.к. все элементы симметрии пересекаются, по крайней мере, в одной точке.

 

Генераторы и подгруппы.

В приведенном выше примере, рассмотрим два элемента C₃ и s_v и найдем результаты произведения их друг с другом и самих на себя (см. табл. 1):

C₃s_v = s_v¢        ;                s_v C₃ = s_v²; C₃ C₃ = C₃ ²       ; s_v s_v = Е.

Т.о. получены все элементы группы. Эти элементы называются генераторами группы. Полное число элементов в группе - порядок группы (в нашем примере порядок равен 6). В рассматриваемом примере операции C₃ и s_v не единственный набор генераторов. Это могут быть и пары (C₃, s_v¢   ), (C₃, s_v²         ), (C₃ ²  , s_v), (C₃ ² , s_v¢   ) и (C₃ ² , s_v²         ). Однако обязательно должна быть одна из осей C₃ или C₃ ²       и одна из плоскостей s_v, s_v¢     или s_v²         . Поэтому эту группы и обозначают как C_3v. Элементы C₃ и C₃ ²   не порождают всю группу. Но они вместе с элементом Е порождают подгруппу точечной группы C_3v. Подгруппа - множество элементов, удовлетворяющее групповым постулатам. [ Показать с использованием табл. 1, что элементы {Е, C₃ и C₃ ²  }составляют группу C₃.] Кроме того, в группе C_3v можно выделить еще три подгруппы {E, s_v}, {E, s_v¢    }и {E, s_v²          }полностью эквивалентные друг другу. Эти подгруппы называются циклическими, т.е. содержат степени одного и того же элемента. Единичный элемент в циклической группе также является степенью указанного элемента.

 

Произведения групп.

Одной из операций, которые могут быть определены для групп, является произведение независимых групп. Если группа А состоит из n элементов, а B из m элементов, то их произведение содержит n´m элементов вида A_iB_j. Например, произведением групп {Е, C₃ и C₃ ²  }и {E, s_v}является:

{Е, C₃, C₃ ²  }´{E, s_v}= (Е, C₃, C₃ ²  , s_v,s_v¢   , s_v²         ) [ рассмотреть подробнее]

Т.о. группа C_3v порождена произведением своих двух независимых подгрупп. В то же время подгруппы {E, s_v}и {E, s_v¢    } не порождают группы:

{E, s_v}´{E, s_v¢    }= (Е, s_v, s_v¢   , C₃ ²         ).

Если мы умножим {E, s_v}´{Е, C₃, C₃ ²  }= (Е, C₃, C₃ ²  , s_v, s_v²          ,s_v¢   ) то получим те же элементы, что и выше, но в другом порядке. Т.к. C₃ и C₃ ²                       не коммутируют с s_v. Произведения групп с некоммутирующими элементами называют полупрямыми (обозначают символом ^). Произведения с коммутирующими элементами называют прямыми (символом ´). Таким образом, если обозначим группу {E, s_v}как C_s, то можно записать, что C_3v = C₃^ C_s .

 

Лекция 3.

Сопряженные элементы и классы.

Два элемента А и В называются сопряженными, если существует элемент R, для которого выполняется соотношение:

A = R B R^-1.

Это означает, что элемент A сопряжен с B относительно R. Аналогичное соотношение для B будет выглядеть, как

B = R^-1 A R.

Здесь B сопряжен с A относительно R^-1. Множество взаимносопряженных элементов в группе называют классом.  Класс может содержат один или несколько элементов. Рассмотрим сопряженные элементы группы C_3v. При помощи таблицы произведений построим таблицу сопряженных элементов.

Таблица 2. Сопряженные элементы.

	B
R	E	C3	C3 2	sv	sv¢	sv²	R-1
E	E	C3	C3 2	sv	sv¢	sv²	E
C3	E	C3	C3 2	sv²	sv	sv¢	C3 2
C3 2	E	C3	C3 2	sv¢	sv²	sv	C3
sv	E	C3 2	C3	sv	sv²	sv¢	sv
sv¢	E	C3 2	C3	sv²	sv¢	sv	sv¢
sv²	E	C3 2	C3	sv¢	sv	sv²	sv²

Каждый элемент таблицы - это элемент A = R B R^-1.

[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно.]

Первый столбец таблицы содержит только один элемент E. Т.е. элемент Е сам по себе образует класс. Каждый из столбцов C₃ и C₃ ² содержит только эти элементы. Поэтому эти два элемента образуют класс. Каждый из трех столбцов s_v содержит только элементы s_v и они также составляют класс. Элементы группы часто обозначают только классами. Например, {E, 2C₃, 3s_v}.