 n=2. a1x1+a1x2<=b1 ГИСЛН – является пересечение всех полуплоскостей соответству
n=2. a1x1+a1x2<=b1 ГИСЛН – является пересечение всех полуплоскостей соответству
a2x1+a2x2<=b2 ющих каждому неравенству системы, таким образом нашли ОДР.
am1x1+am2x2<=bm
Возможные случаи ОДР.
1. ОДР является точка.
2. ОДР выпуклый многоугольник.
3. ОДР выпуклая многоугольная область.
4. ОДР – пустая область
Графический метод.
ГМ состоит из двух этапов.
1) ОДР.
2) Среди всех решений необходимо найти такое решение при котором Z достигает своего либо max или min.
Grad показывает наискорейшее возрастание функции. (С – коэффициент) (линии уровня)
Возможные случаи
1. задача имеет единственное решение.
2. Задача имеет – бесконечно много решений.
3. Задача не имеет решений а) нет ОДР б) в случаи когда zmax - ф-ия не ограниченной сверху линией уровня и наоборот.
Графический метод можно применять если имеется только две переменные или задача может быть приведена с помощью эквивалентных преобразований к задаче с двумя переменными.
ОПОРНЫЙ ПЛАН.
Свойства допустимых планов.
1) Выпуклая линейная комбинация точек. х1 х2 …хk сумма вида α1х1+ α2х2+...+ αkxk, где 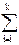 αi =1 (αi>=0 αi – коэффициент линейной комбинации).
αi =1 (αi>=0 αi – коэффициент линейной комбинации).
2) Выпуклым множеством называется такое множество т. Д на плоскости, когда вместе с любыми двумя точками Х1є Д; Х2 є Д принадлежащим множеству Д. Ему принадлежит и их выпуклая Л.К. х=tx1+(1-t)x2 є Д 0<=t<=1
3) Крайняя точка – т.Х выпуклого множества называется крайней если она не может быть представлена в виде выпуклой Л.К. любых двух точек этого множества (n=2)
Опорное решение – это допустимое базисное решение имеющая не более чем m положительных элементов, и причем векторы столбца матрицы соответственно положительны координатам вектора линейны независимы.
Свойства допустимых планов.
Теорема №1
Множество допустимых планов З.Л.П. выпукла если оно не пусто.
Дано: Д- не является пустым множеством – ОДР
Доказать Ж Д- выпуклое множество.
Док-во:
Х1 єД; Х2 єД,то оно удовлетворяет системе ограничений в З.Л.П. Z=cx->max Ax=b X>=0
Ax1=b 0<=t<=1
Ax2=b (1-t) => tAx1+(1-t)Ax2=bt+b(1-t) = A[tx1+(1-t)x2]=b
t>=0
x1; x2>=0 => x>=0
1-t>=0
Ax=b X- решение задачи.
Х = tx1+(1-t)x2 0<=t<=1, согласно опр. Имеем выпуклое множество – Д, т.к. с любыми двумя точками ему принадлежит и их выпуклая Л.К.
Теорема № 2
Если целевая функция имеет максимум на выпуклом многограннике решений, то это максимум достигается в вершине многогранника..
Дано: Zmax->X0 Док-ть X0- вершина.
Zmax=C X0
Док-во: Дан многогранник. А,В,С,Д,Е – вершины. (Док-во проведем от противного)
X0 – не вершина, тогда согласно опр. Крайней точки, X0 – не крайняя точка, и может быть представлена в виде выпуклой Л.К. точек хi є ОДР
C X0>Cxi (т.к. С X0 ->max)
X0 = 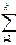 αiXi
αiXi 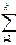 αi=1 αi>=0
αi=1 αi>=0
Найдем значение функции Z=C X0=C 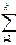 αiXi=
αiXi= 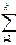 αiCXi<
αiCXi< 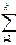 αiCX0=CX0
αiCX0=CX0 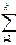 αi=CX0
αi=CX0
В каждом слагаемом сменим Xi на Х0
СХ0<CX0 – противоречие.
Теорема №3
Об альтернативном оптимуме.
Если целвевая функция достигает своего оптимального значения в нескольких вершинах (т) х1 х2 хk, то она достигает оптимального значения в их выпуклой линейной комбинации.
Дано: Док-ть: х= 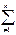 αiXi
αiXi
Xi, i:=1,k 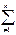 αi=1 αi>=0 CX=d
αi=1 αi>=0 CX=d
Zmax=C{i=d
Док-во
Найдем Z=СХ=C 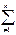 αiXi=
αiXi= 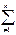 αiCXi=
αiCXi= 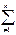 αid=d
αid=d 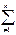 αi=d
αi=d
Теорема № 4
Вектор Х является опорным решением тогда и только тогда, если он является вершиной многогранника.
Если переменных n>3 то говорят гиперплоскость, положение точек в т – мерном пространстве.
ИДЕЯ СИМПЛЕКС МЕТОДА.
Симплекс метод является универсальным.
Симплекс метод – аналитический метод.
1. Находятся первоначальное, опорное решение. А)система ограничений должна быть записана в виде равенств (каноническая форма)
Б)Преобразовать что бы bi >=0 i=1,m
С)Привести систему к единичному базисному виду с неотрицательной правой частью.
Поэтому за разрешающий элемент выбирается строго положительный элемент.
Д)Приравниваем свободные к 0, получаем первоначальное базисное неотрицательное
решение, которое является опорным решением данной задачи и соответствует вершине.
2. Рассматривая функцию цели выясняем является ли полученное решение оптимальным.
3. Если полученное решение не является оптимальным, то необходимо перейти к следующей вершине (опорному решению) Переход осуществляется по определенному правилу по которому: только одна изи базисных переменных должна перейти в свободную и только одна из свободных перейти в базисную.
Алгебра симплекс метода.
| Х1
| Х2
| Х3
| Х4
| Х5
| св.чл
|
| 1
| 0
| 1
| 6
| 2
| 8
|
| 0
| 1
| 1
| 0
| 3
| 9
|
| 0
| 0
| 7
| -1
| -3
| -0
|
| 1
| -2/3
| 1/3
| 6
| 0
| 2
|
| 0
| 1/3
| 1/3
| 0
| 1
| 3
|
| 0
| 1
| 8
| -1
| 0
| 9
|
| 1/6
| -2/18
| 1/18
| 1
| 1/3
|
|
|
|
|
| 0
| 1
| -9
|
| 1/6
| 8/9
| 8 1/8
| 0
| 0
| 1/3
|
Особенность выделенная клетка.
1) Чтобы решать симплекс методом необходимо Z->min (перейти к min)
2) В строке Z записываются коэффициенты ф-ии цели, а свободный член записывается в выделенную клетку св.чл. с противоположным знаком.
3) Сделаем свободные члены неотрицательными.
4) Приводим систему ограничений к единичному базису методом Гауса, выбирая за разрешающий элемент положительный элемент.
5) Функция цели должна быть выражена только через свободные неизвестные, чтобы определить оптимален ли полученный опорный план. Для определения опорного плана свободные элементы =0 r=(7;-1;-3} Среди них выбираем самый отрицательный и делаем разрешающий столбец. Для выбора разрешающей строки находится min-ое из отношений свободных членов системы ограничений к положительным коэффициентам разрешающего столбца
6) Для выбора разрешающей строки находится min-ое из отношений свободных членов системы ограничений к положительным коэффициентам разрешающего столбца.
Альтернативный оптимум.
Предположим найдено оптимальное решение. r>=0. Признаком альтернативного оптимума в этом случаи является равенство 0, хотя бы одной из компонент вектора r. Покажем что если компонента rj =0, для найденого оптимального плана (Х*1) то можно найти еще одно оптимальное решение Х*2, значение в котором будет таким же как и значение в Х*1. Z(Х*2)= Z (Х*1)=Zmin
За разрешающий столбец берем rj =0 Zmin=Z(X*1)=-Q (свободный член в Z) Q1=aij*Q-bi*rj/aij = Q-(bi*rj/aij)=Q bi>0 aij>=0
Сделав шаг метода Гауса, получим новое решение, а значение функции в т Х*2 будет точно таким же как и в Х*2 – т.е. задача Альтернативного оптимума.
Монотонность и конечность алгоритма симплекс метода.
Покажем, что применяя алгоритм симплекс метода к З.Л.П. мы получим, что значение функции монотонно убывает. Предположим, что на кокаком то шаге симплекс метода выбран разрешающий столбец rj<0, а за разрешающую строку выбрана i строка. Покажем что значение функции не возрастает, если мы применим один шаг симплекс метода. Qнов=aij*Q-bi*rj/aij= Q-bi-rj/aij<=0 (bi>=0 rj<0 aij>=0) Qнов>=Q -Qнов<=-Q
Так как многогранник имеет конечное число вершин, то алгоритм симплекс метода будет конечен.
Проблема выражденности.
Если получено в опорном плане число положительных координат меньше чем m, то решение является выражденным, и если полученный план не является оптимальным, т.е. возникает необходимость к новому опорному плану и при этом за разрешающую строку выбирается строка в которой bi=0 Тогда моежт быть проблема зацикливания, т.е. возврат к прежней вершине, для того чтобы избежать этого нужно «расклеить» точки для чего служит ипсилон метод. На ипсилон величину сдвигают прямые, таким образом чтобы раздвигаются вершины. Находят оптимальное решение новой задачи и учитывая ипсилон переходя к страой задаче.
Если в конце преобразований получена таблица, то столбец соответсвующем столбце нет ни одного положительного элемента то Zmin->- бесконечности (нет решения)
Если в результате преобразований сстрока превратилась (0 0 0 0 = 7), то задача не имеет решения по причине не совместимости систем. Нет ОДР.
Если оптимальное решение и соответствующий ему вектор (r) имеет 0 координату то задача на альтернативный оптимум. Что бы найти второе решение берем за разрешающий столбец 0.
Метод искусственного базиса.
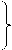 Z=CX->min В данной задаче нет естественного базиса. Введем в каждое ограничение
Z=CX->min В данной задаче нет естественного базиса. Введем в каждое ограничение
Ax=b искусственную переменную «у»>=0 Z преобразуем в T. М – полож. большое чис
X>=0 -Z задача.
Ах+у=b
Х>=0 у>=0
T=CX+M*y->min (М –задача)
Теорема. Если М задача имеет оптимальное решение, то Z – задача: а) тоже имеет решение, если все искусственные переменные = 0. Б) Z- задача не имеет решения если хотя бы одна из искусственных переменных не равна 0, систем ограничений будет не совместна. Если М задача не имеет решения,т.е. Tmin ->-бесконечности, то и Z- задача тоже не имеет решения.
ТЕОРИЯ ДВОЙСТВЕННОСТИ.
Каждой задаче Л.П. можно поставить в соответствие двойственную задачу, решения которой дает немедленное решение прямой задачи.
Стандартная форма.
Z=CX->max
Ax<=b
x>=0 1)
Двойственной задачей к данной З.Л.П. называется задача вида
w=yb->min
YA>=C
Y>=0 2)
Задача 1) и 2) называется пара двойственных задач.
Если по этим правилам построить двойственную задачу к 2) то получим 1). И в этом смысле задачи называются взаимозаменяемыми или сопряженными.
(y- строка)

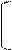 (y1,y2..ym) a11
(y1,y2..ym) a11
a21
am1
Экономический смысл: Экономически двойственную и прямую задачу можно интерпретировать прямая на max прибыль., при выпуске х1 х2 х3, а двойственную min -> расходов на ресурсы.
1) b – сырье; у1 у2 – оценка ресурсов.
Правило построения двойственных задач к общей З.Л.П.
1. Количество переменных в двойственной задаче равно количеству ограничений в прямой задаче.
2. Количество ограничений двойственной задачи равно числу переменных в прямой задачи.
3. Вектор свободных элементов прямой задачи b является вектором коэффициентов двойственной задачи.
4. Вектор коэффициентов функции цели C=(C1…Cn) прямой задачи служит вектором свободных членов системы ограничений двойственной задачи.
5. Если прямой Z->max то в Д.З. W->min/
6. Каждому ограничению – неравенству ai1x1+a12x2+..+ainxm, i=1,m Соответствует неотрицательная переменная yi>=0; i=1,m Д.З.
7. Каждой неотрицательной переменной (xj>=0) j=1,n прямой задачи соответствует ограничения неравенства Д.З. a1jy1+a2jy2+…+amjym>=Cj (j=1,n)
8. Матрица системы ограничений Д.З. служит транспонированная матрица прямой задачи.
9. Каждом ограничению равенству прямой задачи ai1x1+ai2x2+…+ainxn=bi (i=1,m) соответствует свободная переменная yi><0
10. Каждой свободной переменной xj><0 (j=1,n) соответствует ограничение равенства a1j+a2j+…+amjym=Cj
ТЕОРЕМА ДВОЙСТВЕННОСТИ.
1. Если прямая и двойственная задача имеют допустимые решения Х и У, то они имеют оптимальное решение Х* и У* и причем значение функции в этих точках совпадают. Zmax=Wmin CX*=Y*b
Лемма №1
Для любых двух допустимых решений Х и У пары Д.З. справедливо СХ<=Уb
Док-во:
Z=CX->max W=yb->min
Ax<=b YA>=C
x>=0 y>=0
Допустим что X1 – любое допустимое решение П.З., а Y1 – для Д.З.
Тогда Х1 удовлетворяет системе ограничений, т.е. АХ1<=b ¦ y1>=0 Y1A>=C¦x1>=0
Первое ограничение умножим на y1
Y1Ax1<=y1b
Y1Ax1>=Cx1
Cx1<=T<=y1b => Cx1<=y1b
Лемма № 2
Если для допустимых решений X* и У * , выполняется условие равенства СХ* =У*b, то Х* и У* являются оптимальными решениями пары двойственных задач.
Док-во: Дана пара Д.З. Х* и У* допустимые решения. СХ*=У*b, док-ть Х* и У* оптим. решение
Предположим что Х- ОДР (любое), тогда по первой лемме СХ<=У*b, но У*b=Cx* => Cx=Cx* отсюда следует, что Х* т. максимума => у* т. минимума.
На основании графического анализа Д.З. исследовать разрешимость данной задачи в случаи разрешимости – найти экстремальные значение целевой функции.
2 часть теоремы.
Если одна из задач не разрешима из-за не ограниченности функции, то и вторая задача не имеет решения по причине не совместимости систем ограничений.
Док-во:
Согласно первой лемме СХ<=уb, если прямая задача не имеет решения zmax->бесконечности, то, очевидно, что нет такого допустимого решения (у) в котором значение функции было бы больше бесконечности.
ВТОРАЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ И СВОЙСТВА ДВОЙСТВЕННЫХ ОЦЕНОК.
Z=CX->max W=yb->min
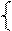 Ax>=b ¦ y1 A- матрица коэффициентов
Ax>=b ¦ y1 A- матрица коэффициентов
x>=0 ¦ y>=0 y1>=c
теорема: Для того что бы допустимое решение Х* и У* пары двойственных задач были оптимальными, необходимо и достаточно, что бы для них выполнялись условия «дополнительное не жесткости»
Z= Cx->max W=yb->min
Ax<=b ¦y YA>=C ¦x
x>=0 y>=0
1. Y*(Ax*-b)=0 (тогда оптимальное решение)
2. (У*А-С)Х*=0
необходимость:
Х* У* - оптимальное решение.
Док-ть: 1 и 2
Док-во: т.к. Х* является оптимальным решением, то и я является допустимым решением => Ах*<=b¦y*>=0 Y*Ax*<=y*b; y* в ходит ОДР => Y*A>=C¦x*>=0 y*Ax*>=Cx* =>
Cx*<=Y*Ax*<=y*b, т.к. х* и у* - оптимальное решение, то Сх*=уb*, по первой теореме => Сх*=у*Ах*=у*b. Ч.т.д
(С-у*А)х*=0
2) (у*А-С)х*=0
1) у*(Ах*-b)=0
достаточность
Дано
1) 2)
Док-ть
Х* и У* - оптим. решение.
Док-во: у*Ах*-у*b=0
Y*Ax*=y*b
y*Ax*-Cx=0
yAx*=Cx*
Cx*=T=y*b=> Cx*=y*b
Вывод для практики: Если в оптимальном решении исходной задачи х*j ><0, то соответствующее ограничение Д.З. превращается в оптимальное решение равенства. Если какое либо из ограничений исходной задачи в оптимальном решении превращается в строгое не равенство, то соответствующая переменная Д.З=0
Свойства двойственных оценок.
В экономике вектор у, называется вектором двойственных оценок или «теневыми ценами». Двойственные оценки сырья и т.д.
Свойства:
1) y*i – является покупателем дефицитности i-го ресурса (i=1,m) Оценка не дефицитного ресурса –0 (y*=0), если 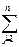 аijxj<bi Чем выше yi (оценка ресурса), тем ресурс дефицитнее.
аijxj<bi Чем выше yi (оценка ресурса), тем ресурс дефицитнее.
2) Y*i=dzmax/dbi y*i=lim ▲Zmax/▲bi (bi->0) => y*i≈▲Zmax/▲bi => Zmax=y*i*▲bi
3) Вектор y*i – является показателем необходимости введения в производство j- технологии Х*j(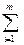 aijy*i-Cj)=0, если
aijy*i-Cj)=0, если 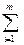 aijy*i>Cj, то выгодно (Cj- цена ед. продукции) =>Х*j=0, то не надо выпускать продукцию Х*j>0, то затраты совпадают с доходами.
aijy*i>Cj, то выгодно (Cj- цена ед. продукции) =>Х*j=0, то не надо выпускать продукцию Х*j>0, то затраты совпадают с доходами.
4) Вектор У является показателем сопоставимости затрат на ресурсы (у*1b1+y*2b2..) со стоимостью продукции.
ТРАНСПОРТНАЯ ЗАДАЧА.
Дадим постановку транспортной задачи в общем виде.
Пусть имеется m- пунктов производства однородного продукта, мощности каждого пункта соответственно = а1 а2 а3 … аь(столбец), имеется n- пунктов потребления данной продукции. Потребности которых составляют соответственно b1 b2 bn (строка) Известны затраты на перевозки единицы продукции из i-го пункта j- потребителю, которые составляют Сij денежных единиц. Требуется спланировать перевозки таким образом что бы суммарные затраты были минимальными.
Математическая модель. Матрица С – матрица затрат. Обозначим через Xij кол-во единиц продукции от i-ог производителя j-потребителю. =>матрица m*n где последний элемент Xmn/ из условия Xij>=0 3)
Предположим что српос = предложению т.е. сумма всех аi= сумме всех bj
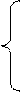
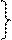 х11+х12+…+х1n =a1
х11+х12+…+х1n =a1
x21+x22+…+x2n =a2 m
2) xm1+xm2+…+xmn = am
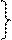 x11+ x21 +xm1 = b1
x11+ x21 +xm1 = b1
x12+ x22+ xm2 = b2 n
x1n+ x2n+ +xmn=bn
1) Z=C11X11+C12X12+…+CmnXmn->min
Бывают задачи типа закрытого и открытого.
А) предположим что спрос >предложения, т.е. сумма ai< суммы bj. Тогда что бы перейти к закрытой задачи вводят фиктивного производителя мощность которого равно am+1= 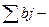
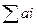 а в транспортно таблице вводится новая строка m+1 в которой am+1=
а в транспортно таблице вводится новая строка m+1 в которой am+1= 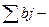
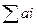 ,а затраты = 0 (Cm+1,j=0)
,а затраты = 0 (Cm+1,j=0)
Б) Если 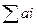 >
> 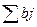 , т.е. предложение выше чем спрос. Вводят фиктивного потребителя bn+1=
, т.е. предложение выше чем спрос. Вводят фиктивного потребителя bn+1= 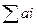 -
- 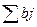 , а в таблице добавляем фиктивный столбец с затратами =0
, а в таблице добавляем фиктивный столбец с затратами =0
Очевидно что Т.З. является Л.П., то можно решить симплекс методом., но таблица которая будет состоять к примеру из 100 столбцов – считать не удобно, то используют такие методы как: распределительный метод, метод дифференциальных рент, метод потенциалов.
Особенности Т.З.
1) Все ограничения равенства (в закрытой)
2) Все переменные входят в систему ограничений, входят в систему либо 0 или 1
3) Каждая переменная входит в С.О. только два раза.
4) Теорема о существовании решения.
Т.З. всегда имеет оптимальное решение если сумма ai= сумме bj.
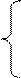 Док-во: Z=
Док-во: Z= 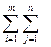 CijXij->min
CijXij->min 
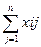 =ai (i=1,m)
=ai (i=1,m)
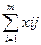 =bj (j=1,n) Xij>=0
=bj (j=1,n) Xij>=0
Очевидно что решением будет Хij = aibj/ 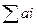 =aibj/
=aibj/ 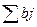
Просуммируем по i: 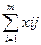 =
= 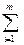 aibj/
aibj/ 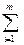 ai = bj
ai = bj 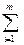 ai/
ai/ 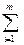 ai = bj
ai = bj
Про суммируем по j: 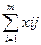 = ai Xij=min(ai;bj)
= ai Xij=min(ai;bj)
ТЕОРЕМА О РАНГЕ МАТРИЦЫ.
Ранг матрицы системы ограничений = m+n-1
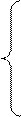
 х11+х12+…+х1n =a1
х11+х12+…+х1n =a1
x21+x22+…+x2n =a2 m
2) xm1+xm2+…+xmn = am
 x11+ x21 +xm1 = b1
x11+ x21 +xm1 = b1
x12+ x22+ xm2 = b2 n
x1n+ x2n+ +xmn=bn
Докажем что ранг матрицы (А)<m+n
А1=(1,1,1,0…0000…000) (коэффициенты первого уравнения размерность m*n)
А2=(0000,1111,0000000)
А1+А2+…+Аm=(111111111111)
Am+1
Am+2 A1+A2+…+Am=Am+1+Am+2+…+Am+n => Векторы линейно зависимые => уравнения
Am+n системы линейно зависимые между собой, а раз они линейно зависимые, то r(A)<m+n
Докажем что ранг = m+n-1
Ранг – наивысший порядок минора отличный от 0.
1) Построим матрицу А из (1 и 0) размерность m*n, найдем минор нужного порядка n-1 вычеркиваем одну из строк. Минор будет равен 1, отличен от 0.
Из этого следует что число базисных неизвестных в Т.З. = m+n-1, а остальные переменные будут свободными. Ч.Т.Д.
Матрица Х=¦Хij¦, называется допустимым решением Т.З. или допустимым планом, если она удовлетворяет системе ограничений и условиям не отрицательности. Допустимый план называется оптимальным, если Z при этом плане принимает свое минимальное значение.
Этапы решения Т.З.
1) Находят первоначальный опорный план, либо методом северо-западного угла, либо методом минимального элемента.
2) Согласно т. о потенциальности плана (оптимальности плана) проверяют полученный план на оптимальность если он оптимален, то записывают ответ X* и Zmin=
3) Если полученный план не оптимален переходят к новому опорному плану.
Метод нахождения первоначального опорного плана.
1) северо-западного угла.
Х11=min(ai;bj) Клетка становится занятой – базисной. Если удовлетворен покупатель то столбец закрывается, если все со склада вывезли то закрывается строка. И.т.д.
Если баланс по строкам и столбцам выполняется и число клеток (занятых) совпадает с рангом матрицы то получаем допустимый план. Но данный опорный план может быть далеким от оптимального, потому что не берутся в расчет расходы. Поэтому используют для этого метод минимального элемента.
Если в середине таблицы одновременно закрывается строка и столбец, а число занятых клеток не равно рангу, то в следующую клетку ставят 0 базисный и клетка считается занятой -> выражденной решение.
Переход от одного опорного плана к другому.
Необходимо перейти к другому опорному решению, т.е. одну из базисных переменных сделать свободной, а одну из свободных занять, так же как и симплекс метод. Для перехода используют замкнутую ломаную линию. Цикл 0 замкнутая ломаная линия вершины которой лежат в клетках а звенья лежат в строках и столбцах. Это ломаная должна быть связной в том смысле что в каждой вершине встречаются только два звена. Циклы могут быть самопересекающимися, при чем т. пересечения не является вершиной.
Цикл пересчета - называется цикл, одна вершина которого лежит в свободной клетке, а остальные в занятой. При переходе от одного плана к другому используются только циклы пересчета. λ>=0 λmin(xij) – i,j нечетные клетки цикла пересчета. Если в цикле пересчета в нескольких клетках разность будет равно 0, то пишут базисный 0.
Проверка плана на оптимальность.
Теорема об оптимальности плана или теорема о потенциальности плана.
Для док-ва составим двойственную к прямой задаче.
 Z=
Z= 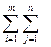 Cijxij->min
Cijxij->min
х11+х12+…+х1n =a1 ¦ -u1
x21+x22+…+x2n =a2 ¦ -u2
xm1+xm2+…+xmn = am ¦ -um
x11+ x21 +xm1 = b1 ¦ V1
x12+ x22+ xm2 = b2 ¦ V2
x1n+ x2n+ +xmn=bn ¦ Vn
xij>=0
V1-u1<=c11 Vm-Un<=C1n
Формулировка: Для того чтобы решения Х состоящее Х=¦xij¦ (i=1,m) (j=1,n) б было оптимальным для Т.З. необходимо и достаточно что бы существовала система из m+n чисел таки что бы выполнялось условия Vj-Ui<=Cij (для свободных клеток) Vj-Ui=Cij (для занятых)
Необходимость Х* - оптим. решение Т.З. Док-ть 1) и 2) условие
Если Х* оптим. решение прямой задачи то по 1-ой т. двойственности существует и решение двойственной задачи, т.е. существуют такие числа Vj & Ui такие что Vj-Ui<=Cij, - 1 условие
Хij(Vj-Ui-Cij)=0 но если клетка занятая то xij>=0 => Vj-Ui=Cij
Достаточность: Дано: Xij>=0 Vj-Ui=Cij
Доктть: Х* оптим решен.
2) -> перенеся Сij в левую часть и * Xij получим 0, это первое условие оптимальности плана поп второй т. двойственности. 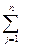 xij=ai ¦ -ui => (суммаXij –ai) ui =0 и (сумма Хij –bi)Vj=0 => второе условие оптимальности. => Х* оптимальное решение.
xij=ai ¦ -ui => (суммаXij –ai) ui =0 и (сумма Хij –bi)Vj=0 => второе условие оптимальности. => Х* оптимальное решение.
Алгоритм потенциалов.
Проверяем Vj-Ui=Cij и Vj-Ui<=Cij
Совместный учет производственных и
Транспортных издержек.
Предположим что имеется m-производителей и n-покупателей.
Ai = (i = 1,m) Bj = (j = 1.n)
Известны производственные затраты di (i = 1,n)
Спланировать перевозки так чтобы суммарные (производственные и транспортные) затраты были минимальными.
Нужно решить обычную транспортную задачу, затраты которой Cij = Cij + d



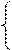 n=2. a1x1+a1x2<=b1 ГИСЛН – является пересечение всех полуплоскостей соответству
n=2. a1x1+a1x2<=b1 ГИСЛН – является пересечение всех полуплоскостей соответству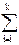 αi =1 (αi>=0 αi – коэффициент линейной комбинации).
αi =1 (αi>=0 αi – коэффициент линейной комбинации).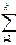 αiXi
αiXi 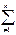 αiXi
αiXi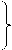 Z=CX->min В данной задаче нет естественного базиса. Введем в каждое ограничение
Z=CX->min В данной задаче нет естественного базиса. Введем в каждое ограничение 
 (y1,y2..ym) a11
(y1,y2..ym) a11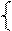 Ax>=b ¦ y1 A- матрица коэффициентов
Ax>=b ¦ y1 A- матрица коэффициентов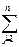 аijxj<bi Чем выше yi (оценка ресурса), тем ресурс дефицитнее.
аijxj<bi Чем выше yi (оценка ресурса), тем ресурс дефицитнее.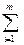 aijy*i-Cj)=0, если
aijy*i-Cj)=0, если 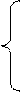
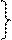 х11+х12+…+х1n =a1
х11+х12+…+х1n =a1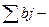
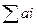 а в транспортно таблице вводится новая строка m+1 в которой am+1=
а в транспортно таблице вводится новая строка m+1 в которой am+1= 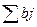 , т.е. предложение выше чем спрос. Вводят фиктивного потребителя bn+1=
, т.е. предложение выше чем спрос. Вводят фиктивного потребителя bn+1= 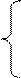 Док-во: Z=
Док-во: Z= 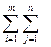 CijXij->min
CijXij->min 
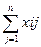 =ai (i=1,m)
=ai (i=1,m)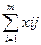 =bj (j=1,n) Xij>=0
=bj (j=1,n) Xij>=0 
 Z=
Z= 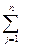 xij=ai ¦ -ui => (суммаXij –ai) ui =0 и (сумма Хij –bi)Vj=0 => второе условие оптимальности. => Х* оптимальное решение.
xij=ai ¦ -ui => (суммаXij –ai) ui =0 и (сумма Хij –bi)Vj=0 => второе условие оптимальности. => Х* оптимальное решение.


