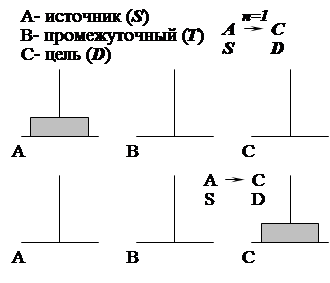Согласно легенде, у жрецов храма Брахмы в горах Тибета есть медная платформа с тремя алмазными стержнями A, B и C. На одном стержне А нанизано 64 золотых диска, каждый из которых немного меньше того, что под ним. Конец света наступит, когда жрецы переместят диски со стержня А на стержень С. Задача имеет следующие условия:
¨ за один раз можно перемещать только один диск,
¨ больший диск нельзя класть на меньший,
¨ снятый диск нельзя отложить, его необходимо сразу же надеть на другой стержень.
Несомненно жрецы все еще работают, т.к. задача включает в себя 264 – 1 ходов. Если тратить по одной секунде на ход, то потребуется примерно 500 миллиардов лет.
Решение данной задачи носит рекурсивный характер. Задача разбивается на последовательность подзадач одного и того же типа, но меньшей размерности. Условием завершения является выполнение простой задачи перемещения одного диска.
Сформулируем алгоритм решения данной задачи для N дисков. Обозначим стержни: начальный (start), промежуточный (temp), конечный или целевой (destination). На начальный стержень нанизано N дисков в порядке возрастания размера, т.е. самый большой диск лежит внизу. Цель задачи – переместить все N дисков с начального стержня на конечный, следуя определенным выше условиям, и распечатать перечень ходов. Предполагается, что промежуточный стержень будет использоваться для временного хранения дисков.
Если N = 1, выполняется условие завершения (базисное условие рекурсивного алгоритма), которое может быть обработано путем перемещения единственного диска с начального стержня на конечный и распечатки соответствующего хода.
Для N > 1 выполняется трехшаговый процесс перемещения N дисков с начального стержня на конечный, причем стержень А является начальным (A – start), стержень В – промежуточным (B – temp), стержень С – конечным (C – dest).
На первом шаге алгоритма перемещаются N – 1 дисков с начального стержня на промежуточный с использованием конечного стержня для временного хранения. При этом стержень А выполняет роль начального (A – start), стержень В выполняет роль конечного (B – dest). Конечный стержень С используется как промежуточный (C – temp).
На втором шаге самый большой диск просто перемещается с начального стержня на конечный: start -> dest.
На третьем шаге N – 1 дисков перемещаются со среднего стержня на конечный с использованием начального стержня для временного хранения. При этом стержень B выполняет роль начального (B – start), стержень C выполняет роль конечного (C – dest). Начальный стержень А используется как промежуточный (A – temp).
Программная реализация алгоритма решения задачи о “ханойских башнях” приведена ниже.
| { перенести N дисков с начального стержня на конечный, используя промежуточный стержень для временного хранения дисков }
|
| Procedure Hanoi(n: byte; start, tmp, dest: char);
|
| begin
|
|
| if (n=1) then
| { условие завершения: перемещение одного диска }
|
| writeln(start, ‘-->’ dest)
|
|
| else begin
|
|
| { перенести N–1 дисков с начального стержня на промежуточный, используя конечный
стержень для временного хранения дисков }
|
| Hanoi(n-1, start, dest, temp);
|
|
| { перенести нижний диск с начального стержня на конечный }
|
| writeln(start, ‘-->’ dest);
|
|
| { перенести N–1 дисков с промежуточного стержня на конечный, используя начальный
стержень для временного хранения дисков }
|
| Hanoi(n-1, temp, start, dest)
|
|
| end;
|
|
| end;
|
|
| | | |
Более короткий вариант решения задачи о “ханойских башнях”:
| { перенести N дисков с начального стержня на конечный, используя промежуточный стержень для временного хранения дисков }
|
| Procedure Hanoi(n: byte; start, tmp, dest: char);
|
| begin
| |
| if (n>0) then begin
| { условие продолжения }
|
| { перенести N–1 дисков с начального стержня на промежуточный, используя конечный
стержень для временного хранения дисков }
|
| Hanoi(n-1, start, dest, temp);
| |
| { перенести нижний диск с начального стержня на конечный }
|
| writeln(start, ‘-->’ dest);
| |
| { перенести N–1 дисков с промежуточного стержня на конечный, используя начальный
стержень для временного хранения дисков }
|
| Hanoi(n-1, temp, start, dest)
| |
| end;
| |
| | | |
Иллюстрация решения задачи для N = 1 диска приведена на рис. 58, для N = 2 дисков приведена на рис. 59, для N = 3 дисков – на рис. 60. Алгоритм требует 2N – 1 ходов.
И все же рекурсивные алгоритмы наиболее эффективны и удобны для обработки рекурсивных структур данных.
Рис. 58. Решение задачи о “ ханойских башнях” для N = 1 диск а
Рис. 59. Решение задачи о “ ханойских башнях” для N = 2 диск ов
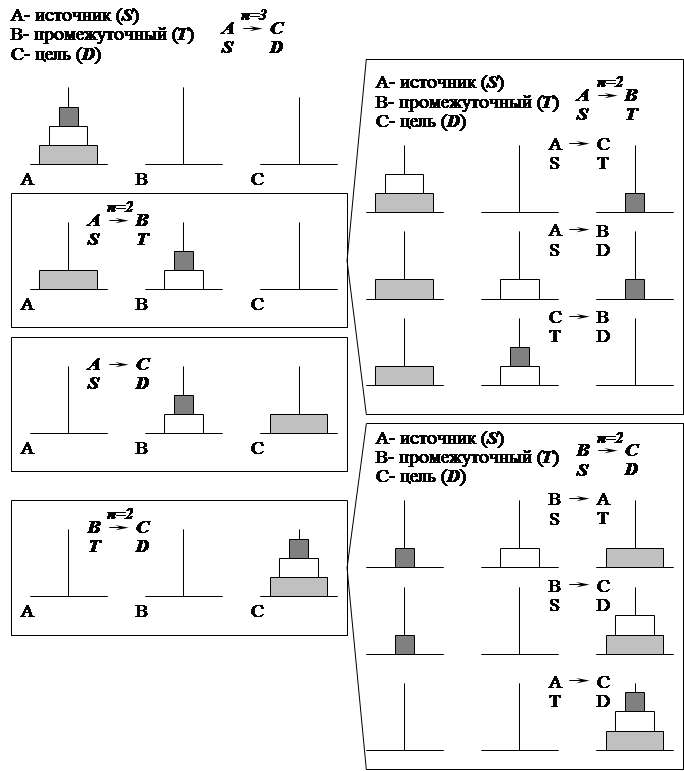
Рис. 60. Решение задачи о “ханойских башнях” для N = 3 дисков