

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Топ:
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Мы уже говорили о том, что в каждом базисе линейного пространства 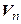 квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.
квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.
Каноническим видом квадратичной формы называется такой ее вид, в котором коэффициенты при произведениях разноименных переменных равны 0, т. е. 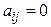 при
при  .
.
Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или –1. Все отличные от нуля коэффициенты при квадратах нормального вида комплексной квадратичной формы равны 1.
Теорема 5.6. Для любой квадратичной формы, заданной на линейном пространстве 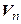 в
в 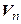 существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.
существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.
Или другая формулировка этой же теоремы:
Для любой квадратичной формы от n переменных существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, и существует линейное невырожденное преобразование переменных, приводящее ее к нормальному виду.
Теорему 5.6 мы докажем позже, а сейчас на примере покажем, как привести квадратичную форму к каноническому виду методом, который называется методом Лагранжа или выделения полных квадратов. Он заключается в следующем: выбираем переменную, коэффициент при квадрате которой отличен от 0, и выделяем полный квадрат, включающий в себя все слагаемые с этой переменной. С этой целью записываем перед скобкой число, обратное выбранному коэффициенту, а в скобках – половину производной по выбранной переменной. За скобками остается квадратичная форма, количество переменных которой уже на единицу меньше, с которой поступаем также. После конечного числа шагов получаем канонический вид.
|
|
Пример. ▼
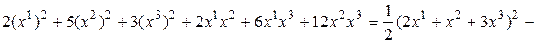
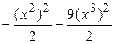
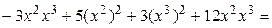
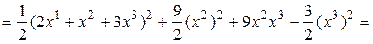
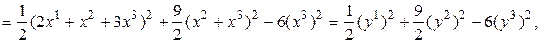
где 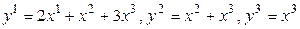 . Матрица этого линейного преобразования запишется так:
. Матрица этого линейного преобразования запишется так:
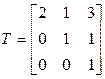 .
.
Как видим, она невырождена, значит, и преобразование переменных является невырожденным. Вводя обозначения
 ,
,
получаем нормальный вид квадратичной формы:  .▲
.▲
Замечания. 1. На самом деле при применении метода Лагранжа получаем не прямое преобразование, приводящее квадратичную форму к каноническому виду, а обратное, т. е. преобразование, которое выражает не старые переменные через новые, а наоборот.
2. Если все коэффициенты при квадратах исходной квадратичной формы равны нулю, а отличен от нуля, например, коэффициент при произведении 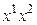 , применим вначале следующее преобразование:
, применим вначале следующее преобразование: 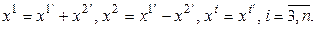 Матрица этого преобразования выглядит так:
Матрица этого преобразования выглядит так:
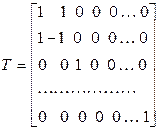 .
.
Очевидно, она невырождена, и поэтому, соответствующее преобразование переменных также будет невырожденным.
Заметим, что канонический вид квадратичной формы определяется неоднозначно, тем не менее, имеет место
Теорема 5. 7 (закон инерции). Все канонические виды одной квадратичной формы на действительном линейном пространстве имеют одинаковое число положительных коэффициентов и одинаковое число отрицательных коэффициентов. Нормальный вид квадратичной формы определяется однозначно с точностью до порядка следования коэффициентов.
►Доказательство достаточно провести для нормального вида.
Пусть в базисе 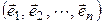 линейного пространства
линейного пространства 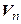 квадратичная форма
квадратичная форма 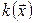 имеет вид
имеет вид
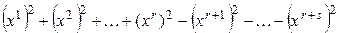 , (5.21)
, (5.21)
а в базисе 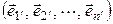 – вид
– вид
 . (5.22)
. (5.22)
Так как 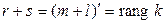 , то достаточно показать, что
, то достаточно показать, что 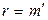 . Предположим, что это не так. Пусть, например,
. Предположим, что это не так. Пусть, например, 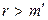 . Обозначим
. Обозначим
 ,
,  .
.
Так как 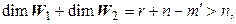 а
а 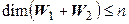 , то сумма
, то сумма  не прямая, поэтому
не прямая, поэтому 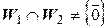 , следовательно,
, следовательно, 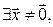
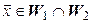 . Так как
. Так как 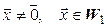 , то из (5.21) видно, что
, то из (5.21) видно, что 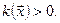 Но так как
Но так как 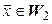 , то из (5.22) видно, видно, что
, то из (5.22) видно, видно, что 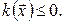 Итак, мы пришли к противоречию. Таким образом,
Итак, мы пришли к противоречию. Таким образом, 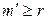 . Аналогично доказывается, что
. Аналогично доказывается, что 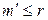 , значит,
, значит, 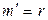 .◄
.◄
|
|
Замечание. Для квадратичных форм на комплексном линейном пространстве нормальный вид, очевидно, определяется однозначно, так как количество отличных от нуля коэффициентов совпадает с рангом квадратичной формы.
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!