ГЛАВА 5. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Билинейные формы
Определение билинейной формы и ее различные формы записи
Определение. Билинейной формой на линейном пространстве 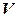 над полем
над полем  называется функция
называется функция 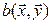 двух векторных аргументов, принимающая значения из поля
двух векторных аргументов, принимающая значения из поля  , линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям.
, линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям.
1*. 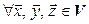 :
: 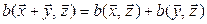 ;
;
2*. 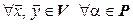 :
: 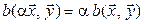 ;
;
3*. 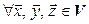 :
: 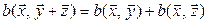 ;
;
4*. 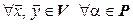 :
: 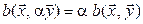 .
.
Рассмотрим n -мерное линейное пространство 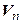 и выберем в нем какой-либо базис:
и выберем в нем какой-либо базис:
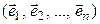 (5.1)
(5.1)
Каждый вектор пространства 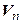 можно разложить по этому базису:
можно разложить по этому базису: 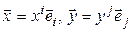 . Тогда
. Тогда
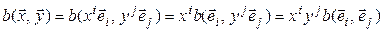 . (5.2)
. (5.2)
Из (5.2) видно, что значение билинейной формыдля любых двух векторов 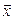 и
и 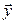 выражается через координаты этих векторов и некоторые числа
выражается через координаты этих векторов и некоторые числа 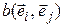 , которые с аргументами
, которые с аргументами 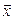 и
и 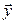 не связаны, а зависят только от выбранного базиса. Обозначим
не связаны, а зависят только от выбранного базиса. Обозначим
 . (5.3)
. (5.3)
Из (5.2) вытекает
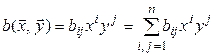 . (5.4)
. (5.4)
Равенство (5.4) называется координатной формой записи билинейной формы.
Определение. Матрицей билинейной формы 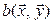 в базисе (5.1) называется матрица
в базисе (5.1) называется матрица  , где
, где  .
.
Обозначим, как обычно,
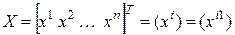 ,
, 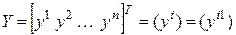 –
–
координатные столбцы векторов 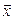 и
и 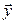 соответственно в заданном базисе. Заметим, что
соответственно в заданном базисе. Заметим, что 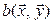 – число, которое можно рассматривать как матрицу размеров
– число, которое можно рассматривать как матрицу размеров  . В таком случае (5.4) можно переписать и так:
. В таком случае (5.4) можно переписать и так: 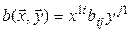 , откуда получаем
, откуда получаем
 . (5.5)
. (5.5)
Это равенство называется матричной формой записи билинейной формы.
Итак, если в 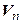 задан базис, то каждой билинейной форме на линейном пространстве
задан базис, то каждой билинейной форме на линейном пространстве 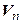 соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.
соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.
Теорема 5.1. Пусть в линейном пространстве 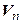 задан какой-либо базис (5.1). Тогда для любой квадратной матрицы
задан какой-либо базис (5.1). Тогда для любой квадратной матрицы 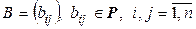 , на линейном пространстве
, на линейном пространстве 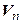 существует единственная билинейная форма
существует единственная билинейная форма 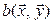 , матрица которой в заданном базисе совпадает с В, т. е. такая, для которой выполняется условие 5.3).
, матрица которой в заданном базисе совпадает с В, т. е. такая, для которой выполняется условие 5.3).
► Построение. Положим по определению:
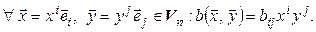
Линейность.
 :
:
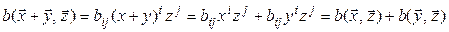 ;
;
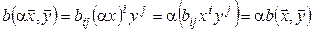 .
.
Таким образом, линейность 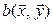 по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.
по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.
Выполнение условия (5.3). Так как 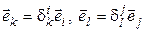 (т. е. i -я координата вектора
(т. е. i -я координата вектора 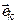 равна
равна 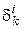 , а j- я координата вектора
, а j- я координата вектора  –
– 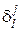 ), то
), то  .
.
Единственность. Предположим, что существует еще одна билинейная форма 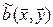 , не совпадающая с формой
, не совпадающая с формой 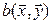 , для которой выполняется (5.3). Тогда
, для которой выполняется (5.3). Тогда
 ,
,
и мы пришли к противоречию.◄
Таким образом, если в 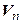 задан какой-либо базис, то между множеством билинейных форм на линейном пространстве
задан какой-либо базис, то между множеством билинейных форм на линейном пространстве 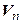 и множеством квадратных матриц n -го порядка с элементами из поля Р устанавливается
и множеством квадратных матриц n -го порядка с элементами из поля Р устанавливается
взаимно однозначное соответствие.
Квадратичные формы
Определение.Квадратичной формой, соответствующей симметричной билинейной форме 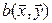 на линейном пространстве V, называется функция одного векторного аргумента
на линейном пространстве V, называется функция одного векторного аргумента 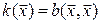 .
.
Пусть задана квадратичная форма 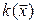 ,
, 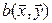 – соответствующая ей симметричная билинейная форма. Тогда
– соответствующая ей симметричная билинейная форма. Тогда
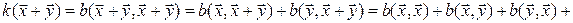
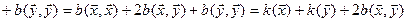
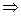
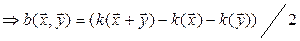 ,
,
откуда вытекает, что по квадратичной форме соответствующая ей симметричная билинейная форма тоже определяется однозначно. Итак, между симметричными билинейными и квадратичными формами на линейном пространстве V устанавливается взаимно однозначное соответствие, поэтому квадратичные формы можно изучать с помощью симметричных билинейных форм.
Рассмотрим n -мерное линейное пространство 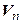 . Матрицей квадратичной формы в заданном базисе линейного пространства
. Матрицей квадратичной формы в заданном базисе линейного пространства 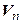 называется матрица соответствующей ей симметричной билинейной формы в том же базисе. Матрица квадратичной формы всегда симметрична.
называется матрица соответствующей ей симметричной билинейной формы в том же базисе. Матрица квадратичной формы всегда симметрична.
Обозначим 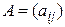 матрицу квадратичной формы в некотором базисе пространства
матрицу квадратичной формы в некотором базисе пространства 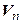 . Если, как обычно, обозначить Х координатный столбец вектора
. Если, как обычно, обозначить Х координатный столбец вектора 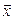 в том же базисе, то из равенства 5.5 получаем матричную форма записи квадратичной формы:
в том же базисе, то из равенства 5.5 получаем матричную форма записи квадратичной формы:
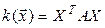 .
.
Теорема 5.4. Пусть в линейном пространстве 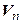 заданы два базиса
заданы два базиса
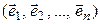 (5.10)
(5.10)
и
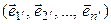 , (5.11)
, (5.11)
и пусть 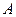 и
и 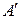 – матрицы квадратичной формы
– матрицы квадратичной формы 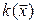 в базисах (5.10) и (5.11) соответственно. Тогда
в базисах (5.10) и (5.11) соответственно. Тогда 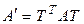 , где Т – матрица перехода от (5.10) к (5.11).
, где Т – матрица перехода от (5.10) к (5.11).
Доказательство вытекает из теоремы 5.2 и определения матрицы квадратичной формы.
В связи с тем, что матрица перехода Т является невырожденной, то при переходе к новому базису ранг матрицы квадратичной формы не меняется. Поэтому можно сформулировать следующее определение.
Определение. Рангом квадратичной формы, заданной на линейном пространстве 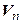 , называется ранг ее матрицы в некотором, а значит, и в любом базисе пространства
, называется ранг ее матрицы в некотором, а значит, и в любом базисе пространства 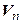 (обозначается
(обозначается 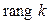 ).
).
Теперь запишем квадратичную форму в координатном виде. Для этого вектор 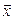 разложим по базису (5.10):
разложим по базису (5.10): 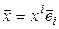 . Если
. Если 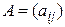 – матрица квадратичной формы
– матрица квадратичной формы 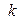 в том же базисе, то в соответствии с равенством (5.4)имеем
в том же базисе, то в соответствии с равенством (5.4)имеем
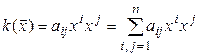 – (5.12)
– (5.12)
координатная форма записи квадратичной формы. Распишем (5.12) подробно при n = 3, учитывая, что 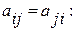
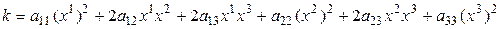 . (5.13)
. (5.13)
Итак, если в 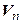 задан базис, то квадратичная форма в координатной записи выглядит как однородный многочлен второй степени от n переменных – координат вектора в данном базисе. Этот многочлен называется видом квадратичной формы
задан базис, то квадратичная форма в координатной записи выглядит как однородный многочлен второй степени от n переменных – координат вектора в данном базисе. Этот многочлен называется видом квадратичной формы 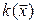 в заданном базисе. Но в приложениях часто такие многочлены возникают самостоятельно, без видимой связи с линейными пространствами (например, вторые дифференциалы функций), поэтому мы сформулируем еще одно определение квадратичной формы.
в заданном базисе. Но в приложениях часто такие многочлены возникают самостоятельно, без видимой связи с линейными пространствами (например, вторые дифференциалы функций), поэтому мы сформулируем еще одно определение квадратичной формы.
Определение. Квадратичной формой от n переменных 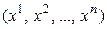 называется однородный многочлен второй степени от этих переменных, т. е. функция вида (5.12). Матрицей квадратичной формы (5.12) называется симметричная матрица
называется однородный многочлен второй степени от этих переменных, т. е. функция вида (5.12). Матрицей квадратичной формы (5.12) называется симметричная матрица 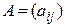 .
.
Пример составления матрицы квадратичной формы. Пусть
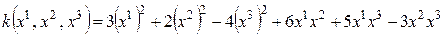 . (5.14)
. (5.14)
Из (5.12) и (5.13) видно, что коэффициент при 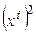 совпадает с
совпадает с 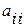 , т.е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что
, т.е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что 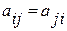 – половина коэффициента при произведении
– половина коэффициента при произведении 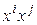 . Таким образом, матрица квадратичной формы (5.14) выглядит так:
. Таким образом, матрица квадратичной формы (5.14) выглядит так:
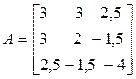 .
.
Выберем теперь в пространстве 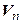 опять два базиса (5.10) и (5.11) и обозначим, как обычно,
опять два базиса (5.10) и (5.11) и обозначим, как обычно, 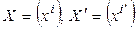 – координатные столбцы вектора
– координатные столбцы вектора 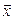 в базисах (5.10) и (5.11) соответственно. При переходе от базиса (5.10) к базису (5.11) координаты вектора меняются по закону:
в базисах (5.10) и (5.11) соответственно. При переходе от базиса (5.10) к базису (5.11) координаты вектора меняются по закону:
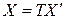 , (5.15)
, (5.15)
где 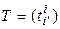 - матрица перехода от (5.10) к (5.11). Заметим, что матрица
- матрица перехода от (5.10) к (5.11). Заметим, что матрица 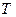 – невырожденная. Запишем равенство (5.15) в координатной форме:
– невырожденная. Запишем равенство (5.15) в координатной форме:
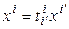 , (5.16)
, (5.16)
или подробно:
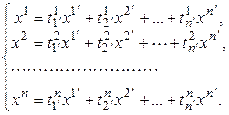 (5.17)
(5.17)
С помощью равенства (5.17) (или (5.16), что одно и то же) от переменных 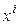 переходим к переменным
переходим к переменным 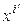 .
.
Определение. Линейным невырожденным преобразованием переменных называется преобразование переменных, заданное системой равенств (5.16) или (5.17), или одним матричным равенством (5.15), при условии, что 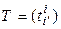 – невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.
– невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.
Если в (5.12) вместо переменных 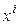 подставить их выражения через переменные
подставить их выражения через переменные 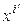 по формулам (5.17), раскрыть скобки и привести подобные, то получим другой однородный многочлен второй степени:
по формулам (5.17), раскрыть скобки и привести подобные, то получим другой однородный многочлен второй степени:
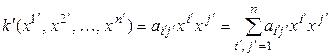 .
.
В этом случае говорят, что линейное невырожденное преобразование переменных (5.17) переводит квадратичную форму 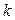 в квадратичную форму
в квадратичную форму 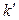 . Значения переменных
. Значения переменных 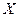 и
и 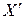 , связанные соотношением (5.15) (или соотношениями (5.16) либо (5.17)), будем называть соответствующими при заданном линейном невырожденном преобразовании переменных.
, связанные соотношением (5.15) (или соотношениями (5.16) либо (5.17)), будем называть соответствующими при заданном линейном невырожденном преобразовании переменных.
Определение. Набор переменных называется нетривиальным, если в нем значение хотя бы одной из переменных отлично от нуля. В противном случае набор переменных называется тривиальным.
Лемма 5.2. При линейном невырожденном преобразовании переменных тривиальному набору переменных соответствует тривиальный набор.
►Из равенства (5.15), очевидно, вытекает: если 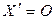 , то и
, то и 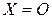 . С другой стороны, используя невырожденность матрицы Т, опять же из (5.15) получаем
. С другой стороны, используя невырожденность матрицы Т, опять же из (5.15) получаем 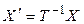 , откуда видно, что при
, откуда видно, что при 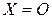 , также и
, также и 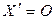 .◄
.◄
Следствие. При линейном невырожденном преобразовании переменных нетривиальному набору переменных соответствует нетривиальный набор.
Теорема 5.5. Если линейное невырожденное преобразование (5.15) переводит квадратичную форму 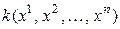 с матрицей А в квадратичную форму
с матрицей А в квадратичную форму 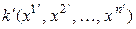 с матрицей А', то
с матрицей А', то 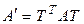 (другая формулировка теоремы 5.4).
(другая формулировка теоремы 5.4).
Следствие. При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака.
Замечание. В отличие от матрицы перехода и матрицы линейного оператора, матрица линейного невырожденного преобразования переменных пишется не по столбцам, а по строкам.
Пусть заданы два линейных невырожденных преобразования переменных:
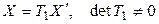 , (5.18)
, (5.18)
и
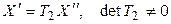 . (5.19)
. (5.19)
Применим их последовательно:
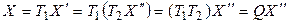 . (5.20)
. (5.20)
Композицией линейных невырожденных преобразований переменных (5.18) и (5.19) называется их последовательное применение, т. е. преобразование переменных 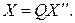 Из (5.20) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.
Из (5.20) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.
Определение. Квадратичные формы называются эквивалентными, если существует линейное невырожденное преобразование переменных, переводящее одну из них в другую.
Квадратичных форм
Назовем r -м усечением квадратичной формы
 (5.24)
(5.24)
квадратичную форму  . Пусть
. Пусть
 –
–
матрица квадратичной формы (5.24). Главными минорами матрицы А называются ее миноры, расположенные в левом верхнем углу. Будем обозначать  главный минор r -го порядка матрицы А. Очевидно, что
главный минор r -го порядка матрицы А. Очевидно, что  совпадает с определителем матрицы квадратичной формы
совпадает с определителем матрицы квадратичной формы 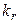 .
.
Теорема 5.9 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительными. Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы нечетного порядка были отрицательными, а четного – положительными.
► Доказательство для положительной определенности.
Необходимость. Дано: квадратичная форма положительно определена. Тогда для любого нетривиального набора переменных 
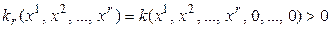 , значит, положительно определена и квадратичная форма
, значит, положительно определена и квадратичная форма 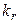 , и поэтому
, и поэтому  , на основании следствия к теореме 5.8.
, на основании следствия к теореме 5.8.
Достаточность. Дано: 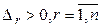 . Доказательство проведем методом математической индукции по количеству переменных.
. Доказательство проведем методом математической индукции по количеству переменных.
1. Проверяем утверждение при 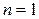 . Имеем
. Имеем 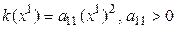 , т. е. квадратичная форма k положительно определена.
, т. е. квадратичная форма k положительно определена.
2. Пусть утверждение верно для квадратичных форм от (n –1)-й переменной. Докажем его для квадратичных форм от n переменных.
Так как 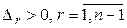 , то, по предположению индукции, квадратичная форма
, то, по предположению индукции, квадратичная форма 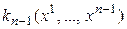 положительно определена, а значит, существует линейное невырожденное преобразование переменных
положительно определена, а значит, существует линейное невырожденное преобразование переменных
 (5.25)
(5.25)
с матрицей 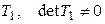 , приводящее
, приводящее  к нормальному виду
к нормальному виду  . Рассмотрим следующее преобразование переменных:
. Рассмотрим следующее преобразование переменных:
 . (5.26)
. (5.26)
Если Т – матрица преобразования (5.26), то 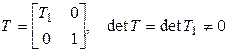 , а значит, (5.26) – линейное невырожденное преобразование переменных. Применив (5.26) к форме (5.24), получаем:
, а значит, (5.26) – линейное невырожденное преобразование переменных. Применив (5.26) к форме (5.24), получаем:
 [(5.26)]
[(5.26)] 
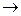

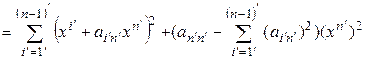 . (5.27)
. (5.27)
Обозначим  и положим
и положим
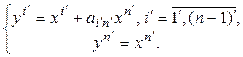 (5.28)
(5.28)
Очевидно, (5.28) – линейное преобразование переменных с матрицей
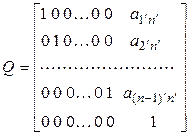 .
.
Так как 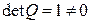 , то (5.28) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (5.27) в квадратичную форму
, то (5.28) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (5.27) в квадратичную форму
 . (5.29)
. (5.29)
Применяя к форме (5.24) композицию преобразований (5.26) и (5.28), получаем квадратичную форму (5.29). Таким образом, (5.29) эквивалентна исходной квадратичной форме (5.24).
Обозначим 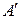 матрицу формы (5.29). Так как при линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака и так как det A =
матрицу формы (5.29). Так как при линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака и так как det A = 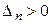 , то
, то
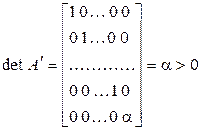 .
.
Поэтому квадратичная форма (5.32) положительно определена согласно теореме 5.8, а значит, положительно определена и исходная квадратичная форма.
Доказательство для отрицательной определенности. Обозначим  ,
, 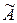 – матрицу квадратичной формы
– матрицу квадратичной формы 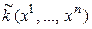 ,
, 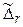 – главные миноры матрицы
– главные миноры матрицы 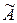 . Тогда
. Тогда
{ k отрицательно определена} 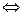 {
{ 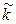 положительно определена}
положительно определена} 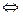
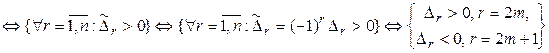 ◄
◄
Замечание. Можно доказать, что если хотя бы один минор четного порядка матрицы квадратичной формы есть число отрицательное, то эта квадратичная форма знаконеопределена.
Определение. Симметричная билинейная форма называется положительно определенной, если положительно определена соответствующая ей квадратичная форма.
ГЛАВА 5. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Билинейные формы



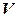 над полем
над полем  называется функция
называется функция 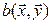 двух векторных аргументов, принимающая значения из поля
двух векторных аргументов, принимающая значения из поля 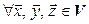 :
: 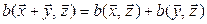 ;
;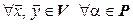 :
: 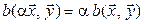 ;
;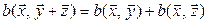 ;
;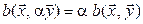 .
.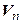 и выберем в нем какой-либо базис:
и выберем в нем какой-либо базис: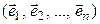 (5.1)
(5.1)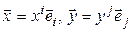 . Тогда
. Тогда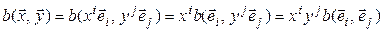 . (5.2)
. (5.2)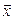 и
и 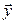 выражается через координаты этих векторов и некоторые числа
выражается через координаты этих векторов и некоторые числа 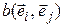 , которые с аргументами
, которые с аргументами  . (5.3)
. (5.3)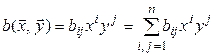 . (5.4)
. (5.4)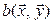 в базисе (5.1) называется матрица
в базисе (5.1) называется матрица  , где
, где 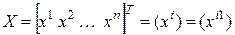 ,
, 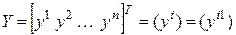 –
– . В таком случае (5.4) можно переписать и так:
. В таком случае (5.4) можно переписать и так: 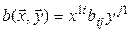 , откуда получаем
, откуда получаем . (5.5)
. (5.5)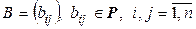 , на линейном пространстве
, на линейном пространстве 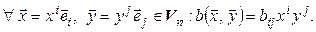
 :
: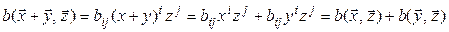 ;
;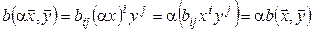 .
.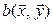 по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.
по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.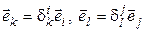 (т. е. i -я координата вектора
(т. е. i -я координата вектора 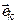 равна
равна 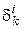 , а j- я координата вектора
, а j- я координата вектора  –
– 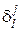 ), то
), то  .
.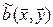 , не совпадающая с формой
, не совпадающая с формой 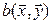 , для которой выполняется (5.3). Тогда
, для которой выполняется (5.3). Тогда ,
,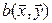 на линейном пространстве V, называется функция одного векторного аргумента
на линейном пространстве V, называется функция одного векторного аргумента 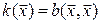 .
.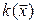 ,
, 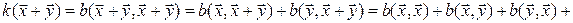
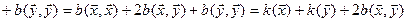
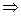
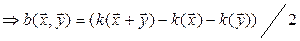 ,
,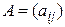 матрицу квадратичной формы в некотором базисе пространства
матрицу квадратичной формы в некотором базисе пространства 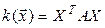 .
. 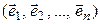 (5.10)
(5.10)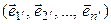 , (5.11)
, (5.11) и
и  – матрицы квадратичной формы
– матрицы квадратичной формы 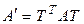 , где Т – матрица перехода от (5.10) к (5.11).
, где Т – матрица перехода от (5.10) к (5.11).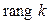 ).
).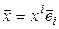 . Если
. Если  в том же базисе, то в соответствии с равенством (5.4)имеем
в том же базисе, то в соответствии с равенством (5.4)имеем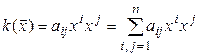 – (5.12)
– (5.12)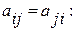
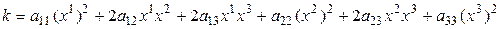 . (5.13)
. (5.13)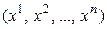 называется однородный многочлен второй степени от этих переменных, т. е. функция вида (5.12). Матрицей квадратичной формы (5.12) называется симметричная матрица
называется однородный многочлен второй степени от этих переменных, т. е. функция вида (5.12). Матрицей квадратичной формы (5.12) называется симметричная матрица 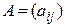 .
.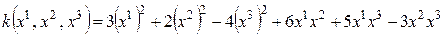 . (5.14)
. (5.14)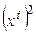 совпадает с
совпадает с 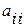 , т.е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что
, т.е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что 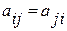 – половина коэффициента при произведении
– половина коэффициента при произведении 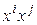 . Таким образом, матрица квадратичной формы (5.14) выглядит так:
. Таким образом, матрица квадратичной формы (5.14) выглядит так: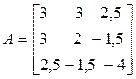 .
.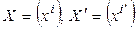 – координатные столбцы вектора
– координатные столбцы вектора 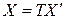 , (5.15)
, (5.15)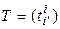 - матрица перехода от (5.10) к (5.11). Заметим, что матрица
- матрица перехода от (5.10) к (5.11). Заметим, что матрица 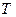 – невырожденная. Запишем равенство (5.15) в координатной форме:
– невырожденная. Запишем равенство (5.15) в координатной форме: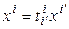 , (5.16)
, (5.16)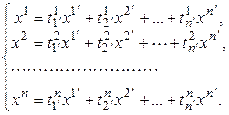 (5.17)
(5.17)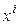 переходим к переменным
переходим к переменным 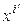 .
.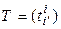 – невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.
– невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.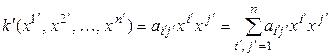 .
.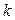 в квадратичную форму
в квадратичную форму  . Значения переменных
. Значения переменных  и
и 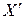 , связанные соотношением (5.15) (или соотношениями (5.16) либо (5.17)), будем называть соответствующими при заданном линейном невырожденном преобразовании переменных.
, связанные соотношением (5.15) (или соотношениями (5.16) либо (5.17)), будем называть соответствующими при заданном линейном невырожденном преобразовании переменных.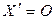 , то и
, то и 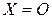 . С другой стороны, используя невырожденность матрицы Т, опять же из (5.15) получаем
. С другой стороны, используя невырожденность матрицы Т, опять же из (5.15) получаем 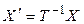 , откуда видно, что при
, откуда видно, что при 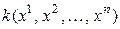 с матрицей А в квадратичную форму
с матрицей А в квадратичную форму 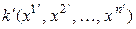 с матрицей А', то
с матрицей А', то 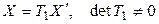 , (5.18)
, (5.18)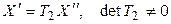 . (5.19)
. (5.19)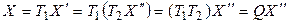 . (5.20)
. (5.20)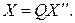 Из (5.20) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.
Из (5.20) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных. (5.24)
(5.24) . Пусть
. Пусть –
– главный минор r -го порядка матрицы А. Очевидно, что
главный минор r -го порядка матрицы А. Очевидно, что 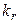 .
.
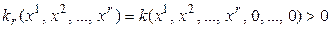 , значит, положительно определена и квадратичная форма
, значит, положительно определена и квадратичная форма  , на основании следствия к теореме 5.8.
, на основании следствия к теореме 5.8.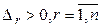 . Доказательство проведем методом математической индукции по количеству переменных.
. Доказательство проведем методом математической индукции по количеству переменных.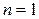 . Имеем
. Имеем 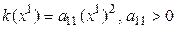 , т. е. квадратичная форма k положительно определена.
, т. е. квадратичная форма k положительно определена.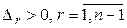 , то, по предположению индукции, квадратичная форма
, то, по предположению индукции, квадратичная форма 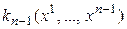 положительно определена, а значит, существует линейное невырожденное преобразование переменных
положительно определена, а значит, существует линейное невырожденное преобразование переменных (5.25)
(5.25)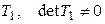 , приводящее
, приводящее  к нормальному виду
к нормальному виду  . Рассмотрим следующее преобразование переменных:
. Рассмотрим следующее преобразование переменных: . (5.26)
. (5.26)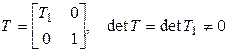 , а значит, (5.26) – линейное невырожденное преобразование переменных. Применив (5.26) к форме (5.24), получаем:
, а значит, (5.26) – линейное невырожденное преобразование переменных. Применив (5.26) к форме (5.24), получаем: [(5.26)]
[(5.26)] 
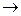

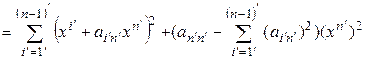 . (5.27)
. (5.27) и положим
и положим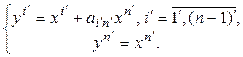 (5.28)
(5.28)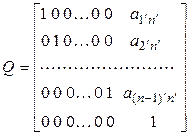 .
.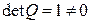 , то (5.28) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (5.27) в квадратичную форму
, то (5.28) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (5.27) в квадратичную форму . (5.29)
. (5.29)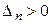 , то
, то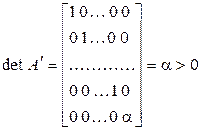 .
. ,
, 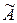 – матрицу квадратичной формы
– матрицу квадратичной формы 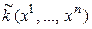 ,
, 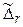 – главные миноры матрицы
– главные миноры матрицы 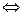 {
{ 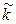 положительно определена}
положительно определена} 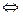
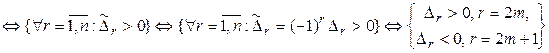 ◄
◄