Данный параграф разбит на пункты, в которых мы попробуем прийти к самому общему доказательству, для случая k последовательностей с n числом переменных, с помощью метода математической индукции.
Доказательство неравенств с минимальным числом переменных
а1*b1 – неравенство с минимальным числом переменных. Тогда
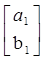 = a1b1.
= a1b1.
Так как это неравенство минимальное из всех существующих, то сравнивать с похожим неравенством его просто невозможно.
Случай с двумя последовательностями из двух переменных
Если 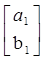 = a1b1. то
= a1b1. то 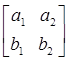 =а1b1+а2b2
=а1b1+а2b2
Теорема 1. Пусть (а1а2) 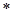 (b 1 b 2) – одномонотонные последовательности. Тогда
(b 1 b 2) – одномонотонные последовательности. Тогда
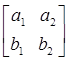
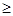
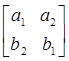
Доказательство
Действительно,
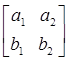 –
– 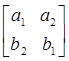 =a1b1+a2b2-a1b2-a2b1 = (a1-a2)
=a1b1+a2b2-a1b2-a2b1 = (a1-a2) 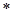 (b1-b2)
(b1-b2)
Так как последовательности (а1а2)(b1b2) одномонотонны, то числа a1-a2 и b1-b2 имеют одинаковый знак. Поэтому
(a1-a2) 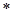 (b1-b2)
(b1-b2) 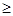 0.
0.
Теорема доказана.
Упражнения
Данные ниже упражнения мы решим с помощью Теоремы 1
Упражнение №1.
Пусть a и b – положительные вещественные числа.
Доказать неравенство
a3 +b3 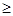 a2b+b2a.
a2b+b2a.
Доказательство.
Заметим, прежде всего, что
a3 +b3 = 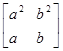 , a2b+b2a =
, a2b+b2a = 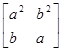
А так как последовательности (a2, b2), (a, b) одномонотонны, то
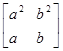
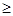
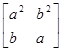
А это значит, что a3 +b3 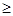 a2b+b2a.
a2b+b2a.
Что и требовалось доказать.
Докажем это же неравенство, но другим способом.
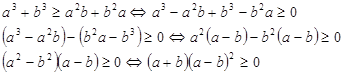
Значит a3 +b3 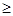 a2b+b2a.
a2b+b2a.
Что и требовалось доказать.
Мы не можем сказать какой из методов доказательства решения легче, так как в данном случае оба метода решения неравенства примерно одинаковые по сложности.
Упражнение №2.
Пусть a и b – положительные вещественные числа.
Доказать неравенство.
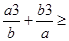 а2+b2.
а2+b2.
Доказательство.
Заметим, прежде всего, что
а2+b2 = 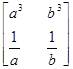 ,
, 
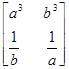 ,
,
А так как последовательности ( ), (
), (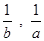 ) одномонотонны, то
) одномонотонны, то
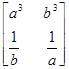
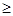
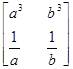 .
.
Что и требовалось доказать.
Случай с двумя последовательностями из трех переменных
Рассмотрим последовательность (а1,а2,а3) и (b 1, b2,b3), и запишем в виде таблицы
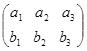
Если последовательность (а1,а2,а3) 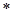 (b1, b2 ,b3) записанных в виде таблицы, где наибольшее из чисел а1,а2,а3 находиться над наибольшим из чисел b 1,b2,b3, а второе по величине а1,а2,а3 находиться над вторым по величине из чисел b 1,b2,b3, и где наименьшее из чисел а1,а2,а3 находиться над наименьшим из чисел b 1,b2,b3 то последовательность одномонотонная.
(b1, b2 ,b3) записанных в виде таблицы, где наибольшее из чисел а1,а2,а3 находиться над наибольшим из чисел b 1,b2,b3, а второе по величине а1,а2,а3 находиться над вторым по величине из чисел b 1,b2,b3, и где наименьшее из чисел а1,а2,а3 находиться над наименьшим из чисел b 1,b2,b3 то последовательность одномонотонная.
Если 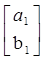 =a1b1, и
=a1b1, и 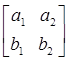 =а1b1+а2b2, то
=а1b1+а2b2, то 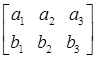 =а1b1+а2b2+a3b3
=а1b1+а2b2+a3b3
Для доказательства следующих теорем нам понадобится одно свойство одномонотонных последовательностей, которое оформим в виде леммы.
Лемма. Если (а1, а2, …а n) и (b 1, b2,… bn) одномонотонные последовательности, то их произведение не изменится при перестановки местами столбцов.
Доказательство.
Рассмотрим последовательность с двумя переменными из двух переменных.
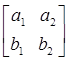 =а1b1+а2b2.
=а1b1+а2b2.
Заметим, что а1b1+а2b2 = а2b2+ а1b1 по переместительному свойству сложения. Значит, в самой таблице мы тоже можем переставлять столбцы переменных, при этом сохраняется одномонотонность последовательности. То есть
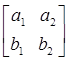 =
= 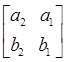
Теперь рассмотрим последовательность с двумя последовательностями из трех переменных.
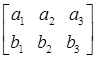 =а1b1+а2b2+a3b3.
=а1b1+а2b2+a3b3.
Кроме того, что мы можем поменять переменные по переместительному свойству, а по сочетательному свойству мы можем объединять некоторые слагаемые, сохраняя одномонотонность последовательности. То есть
а1b1+а2b2+a3b3= (a3b3+а2b2)+ а1b1 = 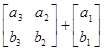
Лемма доказана
Теорема 2. Пусть (а1 а2 а3), (b1 b2 b 3) – одномонотонные последовательности и (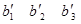 )( здесь и в дальнейшем ) любая перестановка чисел b1 b2 b 3. Тогда
)( здесь и в дальнейшем ) любая перестановка чисел b1 b2 b 3. Тогда
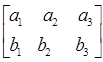

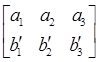 .
.
Доказательство.
Действительно, если последовательность  отличается от (b1 b2 b3) то найдется пара чисел k, l (1
отличается от (b1 b2 b3) то найдется пара чисел k, l (1 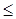 k<l
k<l 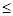 3) такая, что последовательности (ak, al) и (bk, bl) не одномонотонны. Значит, поменяв местами числа
3) такая, что последовательности (ak, al) и (bk, bl) не одномонотонны. Значит, поменяв местами числа 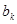 и
и 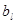 , мы увеличим всю сумму, а значит и всю сумму
, мы увеличим всю сумму, а значит и всю сумму 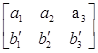 . То есть
. То есть
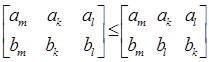 , так как
, так как  .
.
Очевидно, что за конечное число попарных перестановок элементов 2-ой строки можно получить одномонотонную последовательность.
Теорема доказана
Упражнения



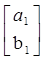 = a1b1.
= a1b1.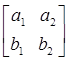 =а1b1+а2b2
=а1b1+а2b2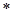 (b 1 b 2) – одномонотонные последовательности. Тогда
(b 1 b 2) – одномонотонные последовательности. Тогда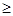
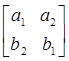
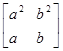 , a2b+b2a =
, a2b+b2a = 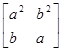
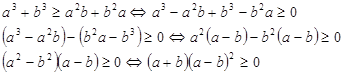
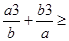 а2+b2.
а2+b2.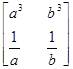 ,
, 
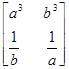 ,
, ), (
), (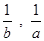 ) одномонотонны, то
) одномонотонны, то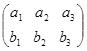
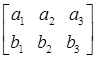 =а1b1+а2b2+a3b3
=а1b1+а2b2+a3b3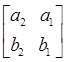
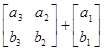
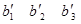 )( здесь и в дальнейшем ) любая перестановка чисел b1 b2 b 3. Тогда
)( здесь и в дальнейшем ) любая перестановка чисел b1 b2 b 3. Тогда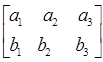

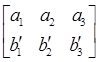 .
. отличается от (b1 b2 b3) то найдется пара чисел k, l (1
отличается от (b1 b2 b3) то найдется пара чисел k, l (1 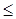 k<l
k<l 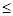 3) такая, что последовательности (ak, al) и (bk, bl) не одномонотонны. Значит, поменяв местами числа
3) такая, что последовательности (ak, al) и (bk, bl) не одномонотонны. Значит, поменяв местами числа 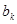 и
и 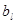 , мы увеличим всю сумму, а значит и всю сумму
, мы увеличим всю сумму, а значит и всю сумму 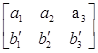 . То есть
. То есть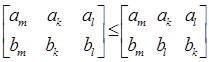 , так как
, так как  .
.


