ВВЕДЕНИЕ
Геофизические методы служат для информационного обеспечения поисков и разведки полезных ископаемых. В настоящее время одним из главных направлений повышения эффективности геофизических работ является повсеместное использование цифровой регистрации и обработки данных геофизических методов. Поэтому всем бакалаврам-геофизикам необходима подготовка в области вычислительной техники. Такую минимальную подготовку призван обеспечить курс «Теоретические основы обработки геофизической информации». Курс посвящен изложению основ теории линейных цифровых процедур, используемых при регистрации и обработке данных. Данные методические указания помогут студентам в освоении теоретических основ физико-математических преобразований временных рядов и применении теории на практике геофизических работ.
Лабораторная работа №1
ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ В ДИСКРЕТНОЙ ФОРМЕ
Цель работы: Ознакомление с различными методами вычисления определенных интегралов. Результаты расчетов позволяют понять способы вычисления различных интегральных преобразований, которые используются при обработке геофизической информации.
Вопросы теории и методики
Получаемая с помощью аналоговой аппаратуры запись каждой сейсмической трассы представляет собой функцию времени и пространства или функцию непрерывного времени вида 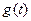 . Такой сигнал называется аналоговым. ЭВМ такое представление сигналов не понимает, поэтому каждую сейсмическую трассу представляют в виде набора цифр двоичного кода: 0 или 1. Двоичный код при оцифровке сейсмического сигнала используется потому, что им удобно моделировать электрические цепи, т.е. если электрический сигнал есть, то записывается 1, нет – 0. Такую процедуру называют дискретизацией сигнала. Дискретизация реализуется в 2 этапа: дискретизации по времени и дискретизации по уровню. Эта процедура является начальной и важной, так как правильно сделанная дискретизация сигнала исключает появление дополнительных помех и неточностей. В дальнейшем дискретный сигнал подвергается различным преобразованиям, которые имеют интегральный вид, а ЭВМ должна посчитать их в дискретном виде. Существуют специальные алгоритмы, которые направлены на решение данной задачи. Данная лабораторная работа знакомит со следующими методами дискретного вычисления определенных интегралов: формулы прямоугольников, трапеций и Симпсона.
. Такой сигнал называется аналоговым. ЭВМ такое представление сигналов не понимает, поэтому каждую сейсмическую трассу представляют в виде набора цифр двоичного кода: 0 или 1. Двоичный код при оцифровке сейсмического сигнала используется потому, что им удобно моделировать электрические цепи, т.е. если электрический сигнал есть, то записывается 1, нет – 0. Такую процедуру называют дискретизацией сигнала. Дискретизация реализуется в 2 этапа: дискретизации по времени и дискретизации по уровню. Эта процедура является начальной и важной, так как правильно сделанная дискретизация сигнала исключает появление дополнительных помех и неточностей. В дальнейшем дискретный сигнал подвергается различным преобразованиям, которые имеют интегральный вид, а ЭВМ должна посчитать их в дискретном виде. Существуют специальные алгоритмы, которые направлены на решение данной задачи. Данная лабораторная работа знакомит со следующими методами дискретного вычисления определенных интегралов: формулы прямоугольников, трапеций и Симпсона.
Формула прямоугольников
Пусть на отрезке 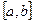 или
или 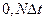 задана непрерывная функция
задана непрерывная функция 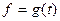 . Требуется представить определенный интеграл
. Требуется представить определенный интеграл  в дискретной форме.
в дискретной форме.
Разделим отрезок 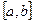 точками
точками 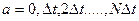 на
на  равных частей длиной
равных частей длиной  (рисунок 1.1)
(рисунок 1.1)
Значения функции 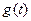 в точках 0, ∆t, 2∆t,…N∆t соответственно
в точках 0, ∆t, 2∆t,…N∆t соответственно 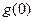 ,
, 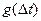 , …..
, ….. 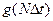 .
.
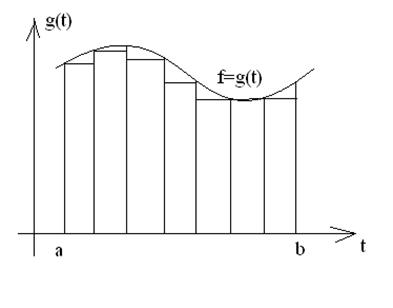
Рисунок 1.1 – Разделение заданной функции на прямоугольники
Из рисунка видно, что любую функцию можно представить в виде набора прямоугольников и площадь всей функции (а смысл интегрирования – это нахождение площади) можно найти, если вычислить площадь каждого прямоугольника в отдельности, а затем все площади сложить, т.е.
 . (1.1)
. (1.1)
Это и есть формула прямоугольников. Если функция 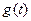 положительная и возрастающая функция, то формула (1.1) выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников. Если нет, то площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников.
положительная и возрастающая функция, то формула (1.1) выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников. Если нет, то площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников.
Формула трапеций
Часто при цифровой обработке сейсмических сигналов для представления определенных интегралов в дискретной форме используется формула трапеций. В соответствии с этой формулой площадь под заданной кривой заменяется суммой площадей трапеций, построенных путем разбиения интервала 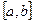 на
на  равных промежутков, на концах которых проведены вертикальные линии до пересечения с заданной кривой (рисунок 1.2).
равных промежутков, на концах которых проведены вертикальные линии до пересечения с заданной кривой (рисунок 1.2).
В соответствии с такой постановкой
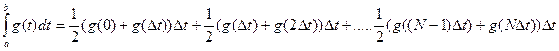 или
или
 . (1.2)
. (1.2)
Это и есть формула трапеций.
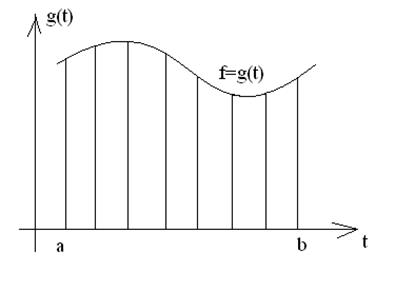
Рисунок 1.2 – Разбиение заданной функции на трапеции
Формула Симпсона
Разделим отрезок 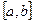 на четное число равных частей
на четное число равных частей  (рисунок 1.3)
(рисунок 1.3)

Рисунок 1.3 – Построение парабол по методу Симпсона
Площадь криволинейной трапеции, соответствующей первым 2 отрезкам 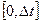 и
и  и ограниченной заданной кривой
и ограниченной заданной кривой 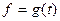 , заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через точки
, заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через точки 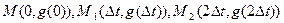 и имеющей ось, параллельную оси
и имеющей ось, параллельную оси 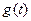 . Такую криволинейную трапецию будем называть параболической трапецией. Уравнение параболы с осью, параллельной оси
. Такую криволинейную трапецию будем называть параболической трапецией. Уравнение параболы с осью, параллельной оси 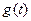 , имеет вид:
, имеет вид:
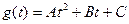 , где А, В, С – коэффициенты, которые однозначно определяются из условия, что парабола проходит через заданные три точки. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
, где А, В, С – коэффициенты, которые однозначно определяются из условия, что парабола проходит через заданные три точки. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
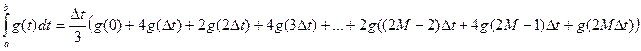 или
или
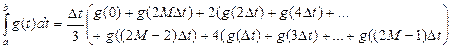 . (1.3)
. (1.3)
Это и есть формула Симпсона.
Задание
1.2.1 Вычислить заданный интеграл аналитически (таблицу 1.1, в соответствии с вариантом).
1.2.2 Построить график подынтегрального выражения в произвольном масштабе.
1.2.3 Пользуясь графиком, вычислить приближенное значение интеграла по формулам (1.1), (1.2), (1.3).
1.2.4 Сравнить значения интеграла, вычисленного разными формулами, сделать выводы.
Содержание отчета
1.3.1 Описание вычисления приближенного значения определенного интеграла в дискретной форме.
1.3.2 Методика расчета
1.3.3 Вычисление интеграла
1.3.4 Выводы, графики, приложения.
1.4 Контрольные вопросы
1.4.1 Какие ошибки возникают при дискретизации по времени?
1.4.2 Объясните смысл дискретизации по уровню и методику выполнения этой процедуры в настоящее время на современных сейсмических станциях? Приведите примеры использования других аппаратных средств дискретизации по уровню.
1.4.3 Как исключить появление ошибок при дискретизации по уровню?
1.4.4 Почему имеется разница в числовых значениях интеграла, вычисленного разными методами?
1.4.5 Объясните теорему Котельникова.
Таблица 1.1
| Номер варианта
| Вид функции
| Номер варианта
| Вид функции
|
| 1
| 
| 11
| 
|
| 2
| 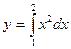
| 12
| 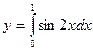
|
| 3
| 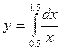
| 13
| 
|
| 4
| 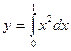
| 14
| 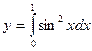
|
| 5
| 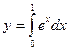
| 15
| 
|
| 6
| 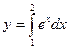
| 16
| 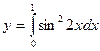
|
| 7
| 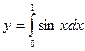
| 17
| 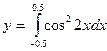
|
| 8
| 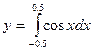
| 18
| 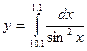
|
| 9
| 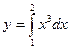
| 19
| 
|
| 10
| 
| 20
| 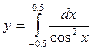
|
Лабораторная работа №2
Вопросы теории и методики
Любую временную функцию практически любой формы, если эта функция удовлетворяет условиям Дирихле, можно представить в виде ряда Фурье:
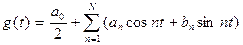 , (2.1)
, (2.1)
где 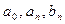 - коэффициенты Фурье.
- коэффициенты Фурье.
Основное свойство ряда Фурье заключается в том, что любую периодическую функцию можно представить в виде набора гармоник с различными частотами, которые будут кратны основной частоте 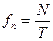 . Чем больше будет количество гармоник, тем лучше будет аппроксимация временной функции.
. Чем больше будет количество гармоник, тем лучше будет аппроксимация временной функции.
Процесс вычисления коэффициентов Фурье называется гармоническим анализом. Эти коэффициенты можно вычислить, используя следующие формулы:
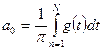 , (2.2)
, (2.2)
 , (2.3)
, (2.3)
 , (2.4)
, (2.4)
Задание
2.2.1 Построить график функции (таблица 2.1) в масштабе в 1 см-0.5 единиц
2.2.2 Просчитать коэффициенты Фурье с помощью формул (2.2-2.4), для заданного количества членов 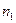 и
и  . Если коэффициенты не равны 0, то можно в расчетах использовать по
. Если коэффициенты не равны 0, то можно в расчетах использовать по 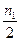 и
и 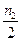 членов.
членов.
2.2.3 Разложить коэффициенты Фурье с помощью формулы (2.1)
2.2.4 Построить график функции с использованием полученного ряда для 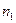 и
и  членов. Вид временной функции, интервалы ее изменений во времени и числа
членов. Вид временной функции, интервалы ее изменений во времени и числа 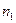 и
и  заданы в таблице 2.1
заданы в таблице 2.1
Содержание отчета
2.3.1 Описание теории разложения функции в ряд Фурье.
2.3.2 Методика разложения в ряд Фурье.
2.3.3 Вычисление Фурье коэффициентов, разложение заданной функции в ряд, вычисление по полученной формуле графика разложенной в ряд функции.
2.3.4 Графики, схемы, приложения.
2.4 Контрольные вопросы
2.4.1 Любую ли функцию можно разложить в ряд Фурье?
2.4.2 Что такое гармонический анализ?
2.4.3 Объяснить смысл разложения в ряд Фурье.
2.4.4 Сделать практический вывод по работе.
Таблица 2.1
| Номер варианта
| Вид функции
| 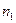
| 
|
| 1
| 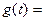 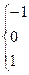 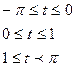
| 2
| 8
|
| 2
| 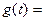  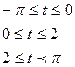
| 2
| 6
|
| 3
| 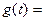 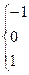 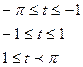
| 4
| 6
|
| 4
| 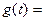 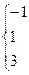 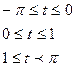
| 2
| 8
|
| 5
| 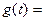 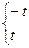 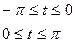  
| 2
| 8
|
| 6
| 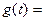 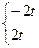 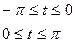 
| 4
| 6
|
Продолжение таблицы 2.1
| Номер варианта
| Вид функции
| 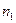
| 
|
| 7
| 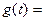 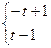 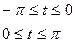  
| 2
| 6
|
| 8
| 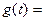 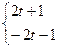 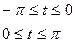 
| 2
| 8
|
| 9
| 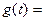 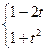 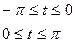
| 2
| 8
|
| 10
| 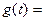 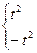 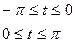
| 2
| 6
|
| 11
| 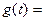 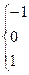 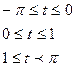
| 2
| 6
|
| 12
| 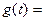 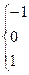 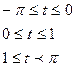
| 2
| 8
|
| 13
| 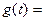 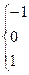 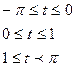
| 2
| 8
|
| 14
| 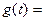 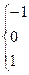 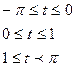
| 2
| 6
|
| 15
| 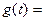 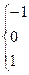 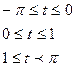
| 2
| 8
|
Примечание: при построении графиков взять шаг 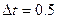
Лабораторная работа № 3
ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Цель работы: Вычисление основного линейного преобразования, наиболее часто используемого при обработке геофизических данных.
Вопросы теории и методики
В том случае, когда мы представляем сейсмическую информацию как изменение во времени амплитуд выходных сигналов, полученных с сейсмоприемников (измеренного в момент взрыва), то мы ведем рассмотрение сейсмического сигнала во временной области, т.е. независимой переменной является время. Однако очень часто бывает необходимым рассматривать сейсмическую волну как результат наложения множества синусоидальных волн, различающихся по частоте, амплитуде и фазе. Соответствующие амплитуды и фазы являются функциями частоты, значит, анализ этих сигналов проводится в частотной области. Функцию, зависящую от частоты, называют спектром или частотной характеристикой.
Основу обработки сейсмических сигналов составляют три вида математических операций, которые являются линейными: преобразование Фурье, свертка, корреляционные функции.
Для того, чтобы пересчитать функцию, зависящую от времени (сейсмическую трассу) в функцию, зависящую от частоты, используют преобразование Фурье. Таким образом, преобразование Фурье используется для трансформации временной функции в соответствующий спектр и наоборот.
Оказывается, что любую временную функцию, которая удовлетворяет условиям Дирихле, а именно:
1) Функция 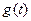 должна быть периодической, т.е. должно выполняться следующее условие
должна быть периодической, т.е. должно выполняться следующее условие 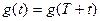 , где Т – период;
, где Т – период;
2) Функция 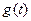 должна иметь конечное число скачков и разрывов;
должна иметь конечное число скачков и разрывов;
3) Функция 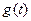 должна иметь конечное число максимумов и минимумов;
должна иметь конечное число максимумов и минимумов;
4) Интеграл функции 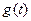 должен сходиться, т.е. иметь решение
должен сходиться, т.е. иметь решение
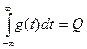 , (3.1)
, (3.1)
где 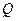 - любое число, можно разложить на простые гармоники с различными частотами. В этом и заключается смысл преобразование Фурье, т.е. это математическое выражение позволяет разложить сложный волновой пакет на простые составляющие с различным частотным составом.
- любое число, можно разложить на простые гармоники с различными частотами. В этом и заключается смысл преобразование Фурье, т.е. это математическое выражение позволяет разложить сложный волновой пакет на простые составляющие с различным частотным составом.
Если имеется временная функция 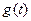 , то в частотную область ее можно перевести в соответствии со следующим интегральным линейным преобразованием
, то в частотную область ее можно перевести в соответствии со следующим интегральным линейным преобразованием
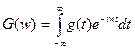 , (3.2)
, (3.2)
где  комплексный спектр временной функции и наоборот, с помощью спектра всегда можно восстановить временную функцию
комплексный спектр временной функции и наоборот, с помощью спектра всегда можно восстановить временную функцию
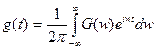 . (3.3)
. (3.3)
Формулы (3.2) и (3.3) описывают соответственно прямое и обратное преобразования Фурье и про эти 2 функции говорят, что они образуют пару преобразований Фурье, т.е. 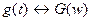 .
.
Спектр функции можно представить и через другие параметры. Например,
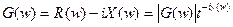 , (3.4)
, (3.4)
где 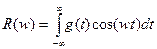 - действительная часть комплексного спектра (3.5)
- действительная часть комплексного спектра (3.5)
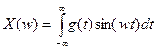 - мнимая часть комплексного спектра (3.6)
- мнимая часть комплексного спектра (3.6)
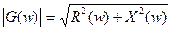 - амплитудный спектр (3.7)
- амплитудный спектр (3.7)
 - фазовый спектр (3.8)
- фазовый спектр (3.8)
Формулы (3.1)-(3.8) применимы к любым видам функций: вещественным, мнимым, четным, нечетным, комбинированным, лишь бы выполнялись условия Дирихле.
Задание
3.2.1 Выбрать временную функцию в соответствии с вариантом (таблица 2.1).
3.2.2 Построить график заданной функции.
3.2.3 Вычислить комплексный спектр 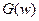 .
.
3.2.4 Вычислить амплитудный и фазовый спектры, сделать выводы.
Содержание отчета
3.3.1 Описание физического смысла спектров.
3.3.2 Методика расчета
3.3.3 Вычисление спектров.
3.3.4 Выводы, графики, приложения.
3.4 Контрольные вопросы
3.4.1 Дать определение всех спектров и объяснить физических смысл каждого.
3.4.2 Как в геофизике используется преобразование Фурье?
3.4.3 Почему в частотной области производить математические преобразования с сейсмическими сигналами легче, чем во временной области?
3.4.4 Докажите с помощью формул, что процедура разложения в ряд Фурье и преобразование Фурье имеют общий математический смысл.
Лабораторная работа №4
Вопросы теории и методики
Основу обработки геофизической информации составляют три вида математических операций: преобразование Фурье, свертка, корреляционные функции.
Свертка
Теория выделения сигналов развита в основном для линейных систем, для которых справедлив принцип суперпозиции. Основываясь на этом принципе, в качестве характеристик линейной системы удобно выбрать ее отклики на входные воздействия некоторых простейших форм. В этом случае вычисление функции отклика системы на входной сигнал сложной формы можно свести к простой схеме:
а) разложение входного сигнала на составляющие выбранной формы, для которых отклик систем известен;
б) вычисление выходного сигнала как сумму откликов системы на все составляющие входного сигнала.
Эта схема применяется при вычислении функции отклика линейной системы, основанном на разложении входного сигнала по единичным импульсам. Это приводит к интегралу свертки
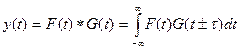 . (4.1)
. (4.1)
Это выражение описывает такие преобразования как фильтрация, сглаживание, интерполирование непрерывных функций. Дискретным аналогом свертки является выражение
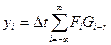 . (4.2)
. (4.2)
Но такая свертка не реализуема, так как эта формула пригодна для бесконечных рядов. На практике количество членов в последовательности конечно. Если временной ряд содержит 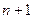 членов, то это значит, что все значения до и после рассматриваемого ряда равны 0
членов, то это значит, что все значения до и после рассматриваемого ряда равны 0
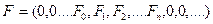
Пусть временной ряд 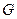 содержит
содержит 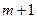 членов, тогда
членов, тогда 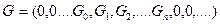 .
.
Пусть 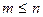 , тогда
, тогда
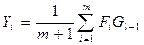 , (4.3)
, (4.3)
где 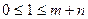 .
.
Однако по этой формуле вычисления содержат слишком много операций, например,
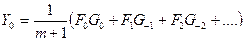 .
.
Для того, чтобы этого избежать на практике используется следующая формула
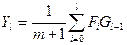 , при
, при 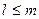 , (4.4)
, (4.4)
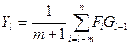 , при
, при 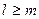 , (4.5)
, (4.5)
Тогда 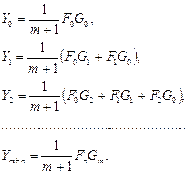
Из последних формул следует, что свертку можно рассматривать, как операцию взаимного сдвига двух временных рядов
Пример: пусть 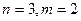
F =
G =
Тогда
| Y0 =
| 
|
| F0
| F1
| F2
| F3
| 
|
|
| G2
| G1
| G0
|
|
|
|
|
| Y1 =
| 
|
| F0
| F1
| F2
| F3
| 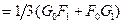
|
|
|
| G2
| G1
| G0
|
|
|
|
| Y2 =
| 
|
| F0
| F1
| F2
| F3
| 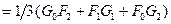
|
|
|
|
| G2
| G1
| G0
|
|
|
| Y3 =
|  F0 F0
| F1
| F2
| F3
| 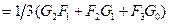
|
|
|
|
|
| G2
| G1
| G0
|
|
|
|
| Y4 =
|  F0 F0
| F1
| F2
| F3
|
| 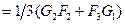
|
|
|
|
| G2
| G1
| G0
|
|
| Y5 =
|  F0 F0
| F1
| F2
| F3
|
|
| 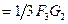
|
|
|
|
|
| G1
| G0
|
|
|
Так рассчитывается свертка двух функций.
В геофизике существуют два подхода к геофизическому сигналу:
А) сигнал детерминированный;
Б) сигнал случайный.
Детерминированными сигналами называются сигналы, которые можно точно предсказать и форма которых может быть заранее известна. Однако на практике сигналы настолько сложны, что предсказать их можно лишь только какими-либо осредненными характеристиками. Бывает так, что сколько бы раз мы не повторяли какой-либо геофизический процесс, выходной сигнал никогда не повторяется, т.е. мы не можем заранее предугадать или прогнозировать появление того или иного выходного сигнала. Такие сигналы называются случайными. Нормальное поле, состоящее из случайных сигналов, обладает замечательной особенностью – оно статистически полностью описывается корреляционными функциями, что дает основание для описания случайных сигналов пользоваться корреляционной теорией. Существуют два вида корреляционных функций: функция автокорреляции (ФАК) и функция взаимной корреляции (ФВК).
ФВК
В непрерывной форме ФВК вычисляется по интегральной формуле следующего вида:
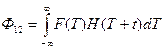 . (4.6)
. (4.6)
Пусть вместо непрерывных функций заданы временные ряды
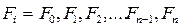 , всего
, всего 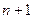 членов;
членов;
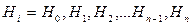 всего
всего 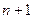 членов.
членов.
Пусть количество отсчетов выходной дискретной ФВК – 1, 2, 3,….m.
В практических задачах m обычно составляет 10-15 % от n. Тогда дискретная ФВК имеет вид:
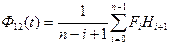 . (4.7)
. (4.7)
Однако часто бывает знать необходимо значения ФВК при отрицательных временах. В этом случае 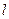 должно принимать как положительные, так и отрицательные значения:
должно принимать как положительные, так и отрицательные значения: 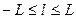 . Если
. Если 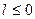 , то формула принимает вид:
, то формула принимает вид:
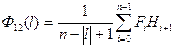 . (4.8)
. (4.8)
Распишем формулы если 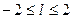 .
.
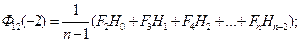

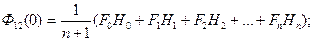
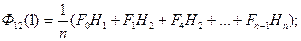
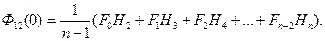
Расчеты по этим формулам можно выполнить как операцию взаимного сдвига.
Пример: пусть заданы временные ряды
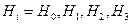
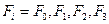
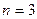
Требуется рассчитать ФВК при 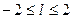 . Тогда
. Тогда
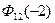 = =
| F0
| F1
| F2
| F3
|
|
| 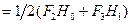
|
|
|
|
| H0
| H1
| H2
| H3
|
|
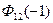 = =
| F0
| F1
| F2
| F3
|
| 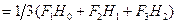
| |
|
|
| H0
| H1
| H2
| H3
|
|
|
| | | | | | | | | |
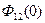 = =
| F0
| F1
| F2
| F3
| 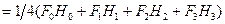
|
|
|
|
| H0
| H1
| H2
| H3
|
|
|
|
 = =
|
| F0
| F1
| F2
| F3
| 
| |
|
| H0
| H1
| H2
| H3
|
|
|
|
| | | | | | | | | |
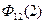 = =
|
|
| F0
| F1
| F2
| F3
| 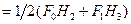
| |
|
| H0
| H1
| H2
| H3
|
|
|
|
|
| | | | | | | | | | |
Результат совпадает с вычисленными по формулам.
4.1.3 ФАК
Вид дискретной функции автокорреляции аналогичен формулам для ФВК. Если  , то
, то
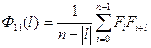 . (4.9)
. (4.9)
Для ФАК справедливы следующие свойства: это функция симметричная, четная, т.е. 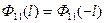 , имеет максимум при
, имеет максимум при 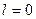 .
.
4.2 Задание
4.2.1 Выберите в соответствии с вариантом временные ряды 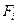 с
с 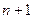 членами,
членами, 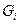 с
с 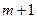 членами и
членами и 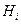 с
с 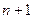 членами (таблица 4.1).
членами (таблица 4.1).
4.2.2 Построить графики функций 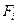 ,
, 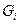 ,
, 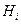 .
.
4.2.3 Рассчитать свертку, как результат взаимного сдвига рядов 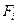 и
и 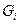 , построить ее график.
, построить ее график.
4.2.4 Рассчитать ФВК, как результат взаимного сдвига рядов 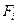 и
и 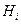 , построить ее график и по графику определить сдвиг между этими рядами в номерах отсчетов
, построить ее график и по графику определить сдвиг между этими рядами в номерах отсчетов 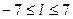 .
.
4.2.5 Рассчитать ФАК, как результат взаимного сдвига ряда 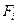 , построить в номерах отсчетов
, построить в номерах отсчетов 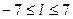 .
.
Содержание отчета
4.3.1 Описание физического смысла рассмотренных преобразований.
4.3.2 Методика расчета
4.3.3 Вычисление свертки и корреляционных функций.
4.3.4 Выводы, графики, приложения.
4.4 Контрольные вопросы
4.4.1 Дать определение свертки, объяснить ее физический смысл и рассказать о том, как эта функция используется при обработке геофизической информации.
4.4.2 Как в геофизике используется ФАК?
4.4.3 Как в геофизике используется ФВК?
4.4.4 Дайте определения корреляционных функций, расскажите об их свойствах.
Лабораторная работа № 5
Содержание отчета
5.3.1 Описание физического смысла рассмотренных преобразований.
5.3.2 Методика расчета
5.3.3 Вычисление фильтра и выходного сигнала.
5.3.4 Выводы, графики, приложения.
5.4 Контрольные вопросы
5.4.1 Что такое рекурсивная фильтрация, дать определение и рассказать об области использования этого фильтра.
5.4.2 Рассказать о методике расчета фильтра и выводе общей формулы для вычисления выходного сигнала рекурсивного фильтра.
Таблица 5.1
| Номер варианта
| Подавляемая частота, Гц
| Шаг дискретизации, мс
| Последовательность входного сигнала 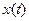
|
| 0
| 20
| 2
| 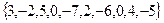
|
| 1
| 30
| 4
| 
|
| 2
| 40
| 6
| 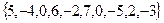
|
| 3
| 50
| 4
| 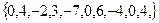
|
| 4
| 60
| 2
| 
|
| 5
| 55
| 4
| 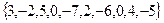
|
| 6
| 45
| 6
| 
|
| 7
| 35
| 4
| 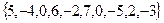
|
| 8
| 25
| 2
| 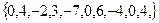
|
| 9
| 65
| 4
| 
|
Лабораторная работа №6
Вопросы теории и методики
Обратная фильтрация относится к классу одноканальных фильтров. Обратной она называется потому, что она направлена на подавление регулярных помех и спектр обратного фильтра обратно пропорционален спектру регулярных помех. Процедура свертки входного сигнала с оператором обратного фильтра называется деконволюцией. Обратные фильтры бывают нескольких видов. Целью фильтра сжатия, является сжатие входного сигнала в единичный импульс. Целью обратного фильтра с прогнозированием является сжатие входного сигнала длиной 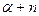 в сигнал длиной
в сигнал длиной 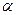 . Целью формирующего или корректирующего обратного фильтра является преобразование входного сигнала в сигнал нужной нам формы. Целью дереверберационного обратного фильтра является подавление многократных волн, появившихся в результате влияния водного слоя.
. Целью формирующего или корректирующего обратного фильтра является преобразование входного сигнала в сигнал нужной нам формы. Целью дереверберационного обратного фильтра является подавление многократных волн, появившихся в результате влияния водного слоя.
Идеальный обратный фильтр во временной области получим из следующего соотношения:
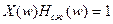 или
или 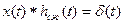 , или
, или 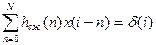 , (6.1)
, (6.1)
где 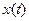 - входной сигнал,
- входной сигнал,
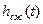 - фильтр сжатия,
- фильтр сжатия,

|
|
|



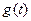 . Такой сигнал называется аналоговым. ЭВМ такое представление сигналов не понимает, поэтому каждую сейсмическую трассу представляют в виде набора цифр двоичного кода: 0 или 1. Двоичный код при оцифровке сейсмического сигнала используется потому, что им удобно моделировать электрические цепи, т.е. если электрический сигнал есть, то записывается 1, нет – 0. Такую процедуру называют дискретизацией сигнала. Дискретизация реализуется в 2 этапа: дискретизации по времени и дискретизации по уровню. Эта процедура является начальной и важной, так как правильно сделанная дискретизация сигнала исключает появление дополнительных помех и неточностей. В дальнейшем дискретный сигнал подвергается различным преобразованиям, которые имеют интегральный вид, а ЭВМ должна посчитать их в дискретном виде. Существуют специальные алгоритмы, которые направлены на решение данной задачи. Данная лабораторная работа знакомит со следующими методами дискретного вычисления определенных интегралов: формулы прямоугольников, трапеций и Симпсона.
. Такой сигнал называется аналоговым. ЭВМ такое представление сигналов не понимает, поэтому каждую сейсмическую трассу представляют в виде набора цифр двоичного кода: 0 или 1. Двоичный код при оцифровке сейсмического сигнала используется потому, что им удобно моделировать электрические цепи, т.е. если электрический сигнал есть, то записывается 1, нет – 0. Такую процедуру называют дискретизацией сигнала. Дискретизация реализуется в 2 этапа: дискретизации по времени и дискретизации по уровню. Эта процедура является начальной и важной, так как правильно сделанная дискретизация сигнала исключает появление дополнительных помех и неточностей. В дальнейшем дискретный сигнал подвергается различным преобразованиям, которые имеют интегральный вид, а ЭВМ должна посчитать их в дискретном виде. Существуют специальные алгоритмы, которые направлены на решение данной задачи. Данная лабораторная работа знакомит со следующими методами дискретного вычисления определенных интегралов: формулы прямоугольников, трапеций и Симпсона. или
или  задана непрерывная функция
задана непрерывная функция 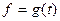 . Требуется представить определенный интеграл
. Требуется представить определенный интеграл  в дискретной форме.
в дискретной форме.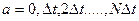 на
на  равных частей длиной
равных частей длиной  (рисунок 1.1)
(рисунок 1.1)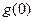 ,
, 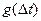 , …..
, ….. 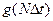 .
.
 . (1.1)
. (1.1)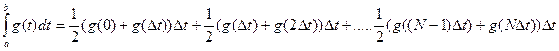 или
или . (1.2)
. (1.2)
 (рисунок 1.3)
(рисунок 1.3)
 и
и  и ограниченной заданной кривой
и ограниченной заданной кривой  и имеющей ось, параллельную оси
и имеющей ось, параллельную оси 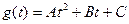 , где А, В, С – коэффициенты, которые однозначно определяются из условия, что парабола проходит через заданные три точки. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
, где А, В, С – коэффициенты, которые однозначно определяются из условия, что парабола проходит через заданные три точки. Сумма площадей параболических трапеций и даст приближенное значение интеграла.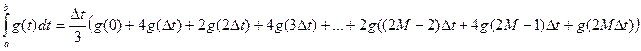 или
или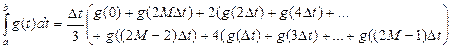 . (1.3)
. (1.3) 

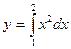
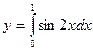
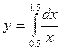

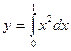
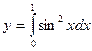
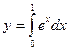

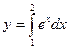
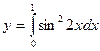
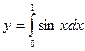
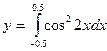
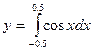
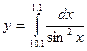
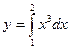


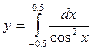
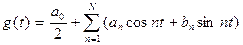 , (2.1)
, (2.1)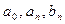 - коэффициенты Фурье.
- коэффициенты Фурье.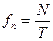 . Чем больше будет количество гармоник, тем лучше будет аппроксимация временной функции.
. Чем больше будет количество гармоник, тем лучше будет аппроксимация временной функции.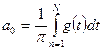 , (2.2)
, (2.2) , (2.3)
, (2.3) , (2.4)
, (2.4)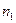 и
и  . Если коэффициенты не равны 0, то можно в расчетах использовать по
. Если коэффициенты не равны 0, то можно в расчетах использовать по 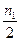 и
и 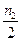 членов.
членов.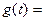
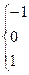
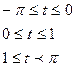

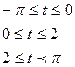
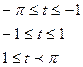
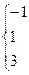
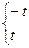
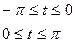

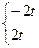
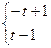
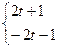
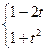
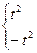
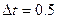
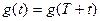 , где Т – период;
, где Т – период;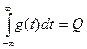 , (3.1)
, (3.1)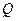 - любое число, можно разложить на простые гармоники с различными частотами. В этом и заключается смысл преобразование Фурье, т.е. это математическое выражение позволяет разложить сложный волновой пакет на простые составляющие с различным частотным составом.
- любое число, можно разложить на простые гармоники с различными частотами. В этом и заключается смысл преобразование Фурье, т.е. это математическое выражение позволяет разложить сложный волновой пакет на простые составляющие с различным частотным составом.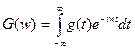 , (3.2)
, (3.2) комплексный спектр временной функции и наоборот, с помощью спектра всегда можно восстановить временную функцию
комплексный спектр временной функции и наоборот, с помощью спектра всегда можно восстановить временную функцию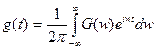 . (3.3)
. (3.3)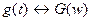 .
.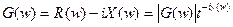 , (3.4)
, (3.4)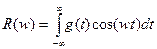 - действительная часть комплексного спектра (3.5)
- действительная часть комплексного спектра (3.5)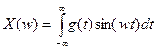 - мнимая часть комплексного спектра (3.6)
- мнимая часть комплексного спектра (3.6)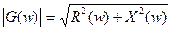 - амплитудный спектр (3.7)
- амплитудный спектр (3.7) - фазовый спектр (3.8)
- фазовый спектр (3.8)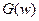 .
.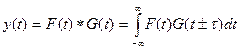 . (4.1)
. (4.1)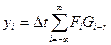 . (4.2)
. (4.2)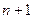 членов, то это значит, что все значения до и после рассматриваемого ряда равны 0
членов, то это значит, что все значения до и после рассматриваемого ряда равны 0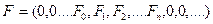
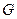 содержит
содержит 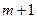 членов, тогда
членов, тогда 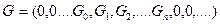 .
.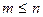 , тогда
, тогда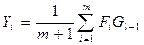 , (4.3)
, (4.3)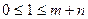 .
.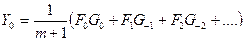 .
.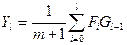 , при
, при 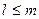 , (4.4)
, (4.4)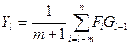 , при
, при 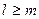 , (4.5)
, (4.5)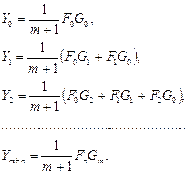
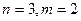
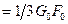
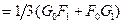
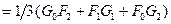
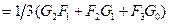
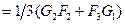
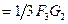
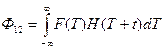 . (4.6)
. (4.6)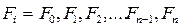 , всего
, всего 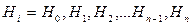 всего
всего 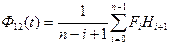 . (4.7)
. (4.7)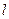 должно принимать как положительные, так и отрицательные значения:
должно принимать как положительные, так и отрицательные значения: 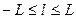 . Если
. Если 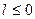 , то формула принимает вид:
, то формула принимает вид: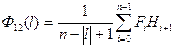 . (4.8)
. (4.8)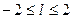 .
.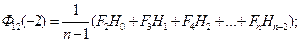

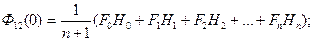
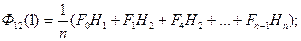
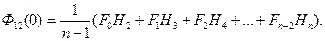
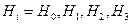
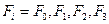
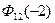 =
=
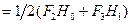
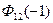 =
=
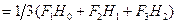
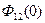 =
=
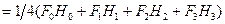
 =
=

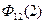 =
=
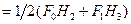
 , то
, то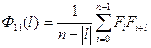 . (4.9)
. (4.9)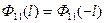 , имеет максимум при
, имеет максимум при 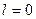 .
.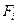 с
с 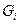 с
с 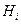 с
с 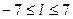 .
.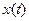
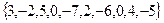

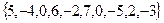
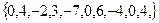

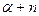 в сигнал длиной
в сигнал длиной 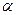 . Целью формирующего или корректирующего обратного фильтра является преобразование входного сигнала в сигнал нужной нам формы. Целью дереверберационного обратного фильтра является подавление многократных волн, появившихся в результате влияния водного слоя.
. Целью формирующего или корректирующего обратного фильтра является преобразование входного сигнала в сигнал нужной нам формы. Целью дереверберационного обратного фильтра является подавление многократных волн, появившихся в результате влияния водного слоя.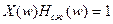 или
или 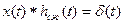 , или
, или 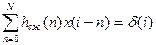 , (6.1)
, (6.1)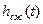 - фильтр сжатия,
- фильтр сжатия,

