Пусть теперь 
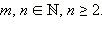 По определению полагают, что
По определению полагают, что 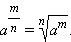
Если же a > 0, то по определению полагают, что 
Понятие нецелой степени отрицательного числа не имеет смысла.
Пример 1
Вычислить
1) 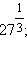
2) 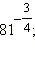
3) 
Решение (Приложение 1)
 Пусть a > 0, b > 0, r, s? любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.
Пусть a > 0, b > 0, r, s? любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.
1. ar · as = ar + s.
2. ar: as = ar - s.
3. (ar) s = ars.
4. ar · br = (ab) r.
5. 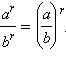
 Пример 2
Пример 2
Упростите выражения
1) 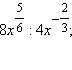
2) 
Решение (Приложение 1)
Степенной функцией с вещественным показателем a называется функция y = xa, x > 0.
Заметим, что для натуральных a степенная функция определена на всей числовой оси, подробнее об этом см. курс "Открытая Математика 2.6. Функции и Графики", параграф 2.4.2. Для произвольных вещественных a это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.
1. К основным свойствам степенной функции y = xa при a > 0 относятся:
2. Область определения функции - промежуток (0; +  ).
).
3. Область значений функции - промежуток (0; +  ).
).
4. Для любых a график функции проходит через точку (1; 1).
5. Функция строго монотонно возрастает на всей числовой прямой, то есть, если 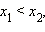 то
то 
6. График степенной функции при a > 0 изображён на рисунке.
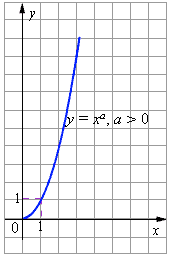
Рисунок 2.2.4.1. Степенная функция y = xa при a > 0

Рисунок 2.2.4.2. Степенная функция y = xa при a < 0
К основным свойствам степенной функции y = xa при a < 0 относятся:
· Область определения функции - промежуток (0; +  ).
).
· Область значений функции - промежуток (0; +  ).
).
· Для любых a график функции проходит через точку (1; 1).
· Функция строго монотонно убывает на всей числовой прямой, то есть если 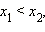 то
то 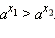
· График степенной функции при a < 0 изображён на рисунке.
Справедливы следующие свойства степенной функции:
· 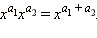
· 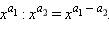
· 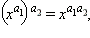 если n > k.
если n > k.
· 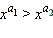 на участке x > 1, если
на участке x > 1, если 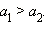
· 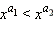 на участке 0 < x < 1, если
на участке 0 < x < 1, если 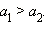
Мы знаем, какой смысл имеет выражение, где a 0, если показатель n — целое число. Например, (–3)5 означает произведение пяти множителей, каждый из которых равен –3. Число 2–6 означает число, обратное степени 26. Введем теперь понятие степени, у которой показатель не целое, а дробное число.
Из определения арифметического корня следует, что если m – целое число, n – натуральное и m делится на n, то при a >0 верно равенство  .
Например, .
Например,  , так как , так как  . Если принять, что равенство . Если принять, что равенство  имеет место и в том случае, когда имеет место и в том случае, когда  — дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано на следующих уроках). — дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано на следующих уроках).
|
|
| Определение: Если a >0,  – дробное число (m – целое, n – натуральное), то – дробное число (m – целое, n – натуральное), то
 . .
|
|
| По определению имеем:
 Степень с основанием, равным нулю, определяется только для положительного дробного показателя:
Степень с основанием, равным нулю, определяется только для положительного дробного показателя:
|
|
| Если  – дробное положительное число (m и n – натуральные), то – дробное положительное число (m и n – натуральные), то  . .
|
|
| Для отрицательных оснований степень с дробным показателем не рассматривается. Такие выражения, как  , не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,75 можно представить в виде дроби так: , не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,75 можно представить в виде дроби так:
 и т. д.
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: как бы оно ни записывалось, результат будет один и тот же. Например: и т. д.
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: как бы оно ни записывалось, результат будет один и тот же. Например:
 .
В общем случае для а >0, m — целого и натуральных n и k получим: .
В общем случае для а >0, m — целого и натуральных n и k получим:
 . .
|
| Пример 1
| Представим степень с дробным показателем в виде корня:
|
|
| а)  ; ;
| в)  ; ;
| д)  ; ;
| б)  ; ;
| г)  ; ;
| е)  . .
| |
| Пример 2
| Представим арифметический корень в виде степени с дробным показателем:
|
|
| |
| Пример 3
| Укажем допустимые значения переменных в выражениях а)  и б) и б)  . .
|
|
| Степень с положительным дробным показателем определена только для неотрицательных оснований, а степень с отрицательным дробным показателем определена только для положительных оснований. Другими словами, основание должно быть положительно, но может равняться нулю при условии, что показатель положителен.
а) 3– b  0; b 0; b  0.
б) a –1>0; a >1. 0.
б) a –1>0; a >1.
|
| Известные свойства степени с целым показателем справедливы и для степени с любым рациональным показателем. Перечислим их:
|
|
| Для любых a >0, b >0 и любых рациональных чисел p и q:
|
|
| Докажем свойство (1). Сначала покажем на частном примере способ докаазательства этого свойства.
Пусть, например, p =  , q = , q =  . Докажем, что . Докажем, что
 Приведем дроби
Приведем дроби  и и  к общему знаменателю: к общему знаменателю:
 Так как
Так как  и и  , то по свойству арифметическкого корня имеем: , то по свойству арифметическкого корня имеем:
 Переходя к степени с дробным показателем, получим:
Переходя к степени с дробным показателем, получим:
 Следовательно,
Следовательно,  . Но . Но  , поэтому , поэтому
 Приведем теперь доказательство свойства (1) в общем виде.
Представим рациональные числа p и q в виде дробей с одинаковыми знаменателями:
Приведем теперь доказательство свойства (1) в общем виде.
Представим рациональные числа p и q в виде дробей с одинаковыми знаменателями:  и и  , где k и m — целые числа, а n — натуральное число. Тогда , где k и m — целые числа, а n — натуральное число. Тогда
 Значит,
Значит,  Из свойства (1) следует, что
Из свойства (1) следует, что
|
|
| для любого положительного a и любого рационального числа p
 . .
|
|
| Действительно,  .
Свойство (2) следует из свойства (1) и определеения частного.
Докажем свойство (3), т. е. докажем, что при a >0 и любых рациональных p и q .
Свойство (2) следует из свойства (1) и определеения частного.
Докажем свойство (3), т. е. докажем, что при a >0 и любых рациональных p и q
 .
Пусть .
Пусть  и и  , где l и m — целые, а k и n — натуральные числа. Тогда , где l и m — целые, а k и n — натуральные числа. Тогда
 Значит,
Значит,  .
Покажем, что .
Покажем, что
|
|
| при любом рациональном p и любом натуральном n
 . .
|
|
| Действительно, по определдению степени с дробным показателем и свойству (3) имеем:
 Докажем свойство (4), т. е. докажем, что при a >0 и b >0 и любом рациональном p
Докажем свойство (4), т. е. докажем, что при a >0 и b >0 и любом рациональном p
 Пусть
Пусть  , где l — целое число и k — натуральное число. Тогда , где l — целое число и k — натуральное число. Тогда
 Значит,
Значит,  Свойство (5) можно доказать, представив дробь
Свойство (5) можно доказать, представив дробь  в виде произведения в виде произведения  и применив затем свойство (4). и применив затем свойство (4).
|
| Пример 1
| Представим в виде степени выражения:
|
|
| |
| Пример 2
| Представим в виде степени выражение  : :
|
|
| 
|
| Пример 3
| Вычислим  . .
|
|
| 
|
| Пример 4
| Найдем значения выражений:
|
|
| а) 
| б) 
| |
Степень с рациональным показателем.
Выражение аn определено для всех а и n, кроме случая а=0 при n≤0. Напомним свойства таких степеней. Для любых чисел а, b и любых целых чисел m и п справедливы равенства:
am*an=am+n;
am:аn=am-n (а≠0);
(аm)n = аmn;
(ab) n = an*bn;
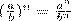 (b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство: Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1. В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа (b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство: Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1. В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа  должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то
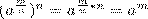 Последнее равенство означает (по определению корня n-й степени), что число
Последнее равенство означает (по определению корня n-й степени), что число  должно быть корнем п-й степени из числа аm. Определение. Степенью числа а>0 с рациональным показателем r= должно быть корнем п-й степени из числа аm. Определение. Степенью числа а>0 с рациональным показателем r=  , где m — целое число, а n — натуральное (n > 1), называется число , где m — целое число, а n — натуральное (n > 1), называется число 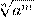 Итак, по определению Итак, по определению
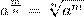 (1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0. Замечание 1. Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число ar положительно. Замечание 2. Любое рациональное число допускает различные записи его в виде дроби, поскольку (1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0. Замечание 1. Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число ar положительно. Замечание 2. Любое рациональное число допускает различные записи его в виде дроби, поскольку  для любого натурального k. Значение arтакже не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что для любого натурального k. Значение arтакже не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что
 Замечание 3. При а < 0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для а<0, то, например, значение
Замечание 3. При а < 0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для а<0, то, например, значение 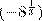 равнялось бы равнялось бы  , т. е. — 2. Но, с другой стороны, , т. е. — 2. Но, с другой стороны,  , и поэтому должно выполняться равенство , и поэтому должно выполняться равенство  . .
| | | | | | |
| Теория вероятностей, математическая статистика |
| Математический форум|
| Для вебмастеров
| |




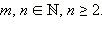 По определению полагают, что
По определению полагают, что 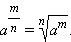

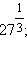
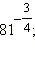

 Пусть a > 0, b > 0, r, s? любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.
Пусть a > 0, b > 0, r, s? любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.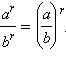
 Пример 2
Пример 2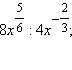

 ).
).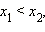 то
то 


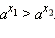
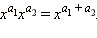
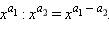
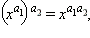 если n > k.
если n > k.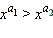 на участке x > 1, если
на участке x > 1, если 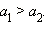
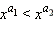 на участке 0 < x < 1, если
на участке 0 < x < 1, если  .
Например,
.
Например,  , так как
, так как  . Если принять, что равенство
. Если принять, что равенство  — дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано на следующих уроках).
— дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано на следующих уроках).
 .
.
 Степень с основанием, равным нулю, определяется только для положительного дробного показателя:
Степень с основанием, равным нулю, определяется только для положительного дробного показателя:
 .
.
 , не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,75 можно представить в виде дроби так:
, не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,75 можно представить в виде дроби так:
 и т. д.
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: как бы оно ни записывалось, результат будет один и тот же. Например:
и т. д.
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: как бы оно ни записывалось, результат будет один и тот же. Например:
 .
В общем случае для а >0, m — целого и натуральных n и k получим:
.
В общем случае для а >0, m — целого и натуральных n и k получим:
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.






 и б)
и б)  .
.
 0; b
0; b 




 , q =
, q =  Приведем дроби
Приведем дроби  Так как
Так как  и
и  , то по свойству арифметическкого корня имеем:
, то по свойству арифметическкого корня имеем:
 Переходя к степени с дробным показателем, получим:
Переходя к степени с дробным показателем, получим:
 Следовательно,
Следовательно,  . Но
. Но  , поэтому
, поэтому
 и
и  , где k и m — целые числа, а n — натуральное число. Тогда
, где k и m — целые числа, а n — натуральное число. Тогда
 Значит,
Значит,  Из свойства (1) следует, что
Из свойства (1) следует, что
 .
.
 .
Свойство (2) следует из свойства (1) и определеения частного.
Докажем свойство (3), т. е. докажем, что при a >0 и любых рациональных p и q
.
Свойство (2) следует из свойства (1) и определеения частного.
Докажем свойство (3), т. е. докажем, что при a >0 и любых рациональных p и q
 .
Пусть
.
Пусть  Значит,
Значит,  .
.
 Докажем свойство (4), т. е. докажем, что при a >0 и b >0 и любом рациональном p
Докажем свойство (4), т. е. докажем, что при a >0 и b >0 и любом рациональном p
 Пусть
Пусть  Значит,
Значит,  и применив затем свойство (4).
и применив затем свойство (4).



 :
:

 .
.



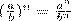 (b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство: Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1. В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа
(b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство: Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1. В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа  должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то
должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то
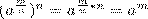 Последнее равенство означает (по определению корня n-й степени), что число
Последнее равенство означает (по определению корня n-й степени), что число  , где m — целое число, а n — натуральное (n > 1), называется число
, где m — целое число, а n — натуральное (n > 1), называется число 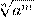 Итак, по определению
Итак, по определению
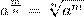 (1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0. Замечание 1. Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число ar положительно. Замечание 2. Любое рациональное число допускает различные записи его в виде дроби, поскольку
(1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0. Замечание 1. Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число ar положительно. Замечание 2. Любое рациональное число допускает различные записи его в виде дроби, поскольку  для любого натурального k. Значение arтакже не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что
для любого натурального k. Значение arтакже не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что
 Замечание 3. При а < 0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для а<0, то, например, значение
Замечание 3. При а < 0 рациональная степень числа а не определяется, и это не случайно. Если бы мы сочли верной формулу (1) и для а<0, то, например, значение 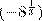 равнялось бы
равнялось бы  , т. е. — 2. Но, с другой стороны,
, т. е. — 2. Но, с другой стороны,  , и поэтому должно выполняться равенство
, и поэтому должно выполняться равенство  .
.



