

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Кроме степеней с рациональными показателями в математике и других точных науках большое значение имеют и степени с иррациональными показателями, однако их определение выходит за рамки курса средней школы. Упомянем лишь о том, что степень с иррациональным показателем строится с помощью предельного перехода по последовательностям степеней с рациональными показателями, которые являются приближениями иррационального показателя степени с недостатком и с избытком.
С понятиями степени с целочисленным показателем и арифметического корня можно ознакомиться в разделе «Степень с целочисленным показателем и арифметический корень» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра "Резольвента" учебными материалами для подготовки к ЕГЭ и ОГЭ (ГИА) по математике.
| Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика "проблемными". Запись по телефону (495) 509-28-10. |
Степень с целым показателем
Выражение  называется степенью с натуральным показателем. Ясно, что
называется степенью с натуральным показателем. Ясно, что 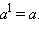 Число a называется основанием степени, а n - показателем степени. Третья степень числа называется кубом, вторая - квадратом. Первой степенью называется само число a.
Число a называется основанием степени, а n - показателем степени. Третья степень числа называется кубом, вторая - квадратом. Первой степенью называется само число a.
В параграфе 1.1.2 было определено понятие степени натурального числа с натуральным показателем. Обобщим это определение на случай произвольного действительного числа.
|
|
Пусть a - любое действительное число; n - натуральное число, большее единицы. n-й степенью числа a называется произведение n множителей, каждый из которых равен a. Если n = 1, то по определению считают, что a 1 = a. Число a называется основанием степени, число n - показателем степени.
Справедливы следующие свойства степени:
1. an · ak = an + k.
2. an: ak = an - k, если n > k.
3. (an) k = ank.
4. an · bn = (ab) n.
5. 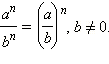
Например, 

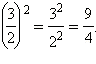
По определению полагают, что a 0 = 1 для любого 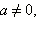 . Нулевая степень числа нуль не определена.
. Нулевая степень числа нуль не определена.
По определению полагают, что если 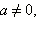 n - натуральное число, то
n - натуральное число, то 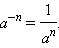
Справедливо равенство  Например,
Например, 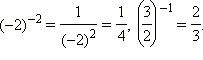
Совершенно аналогично вводится понятие степени рациональных выражений. Чтобы возвести рациональную дробь в натуральную степень, нужно отдельно возвести в эту степень числитель, и отдельно - знаменатель:
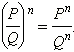
Пример 1
Преобразовать в дробь степень 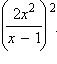
Решение (Приложение 1)
Возведение рациональной дроби в отрицательную степень происходит по следующей формуле: 
Пример 2
Преобразовать в дробь степень 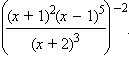
Решение (Приложение 1)
2. Корень n -й степени
Пусть 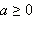 и
и 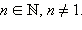 Тогда существует единственное неотрицательное число x такое, что выполняется равенство
Тогда существует единственное неотрицательное число x такое, что выполняется равенство 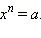 Это число называется арифметическим корнем n-й степени из неотрицательного числа и обозначается
Это число называется арифметическим корнем n-й степени из неотрицательного числа и обозначается  При этом число a называется подкоренным числом, а число n - показателем корня.
При этом число a называется подкоренным числом, а число n - показателем корня.
Вместо слова "корень" часто говорят радикал. Если n = 2, то обычно пишут просто: 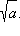 При n = 2 арифметический корень называется квадратным корнем, при n = 3 говорят о кубическом корне.
При n = 2 арифметический корень называется квадратным корнем, при n = 3 говорят о кубическом корне.
Итак, по определению: 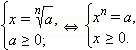
Отсюда следует, что 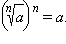 Например,
Например, 
При  справедливы следующие свойства корней.
справедливы следующие свойства корней.
1. 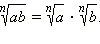
2. 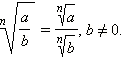
3. 
4. 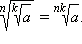
5. 
Если a < 0, а 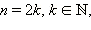 то не существует такого действительного x, при котором бы выполнялось равенство
то не существует такого действительного x, при котором бы выполнялось равенство 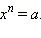 Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть a < 0, а n - нечётное число, тогда существует единственное число x такое, что
Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть a < 0, а n - нечётное число, тогда существует единственное число x такое, что 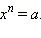 Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же:
Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же:  Например,
Например,  так как
так как 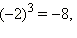
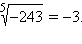 Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.
Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.
|
|
Пример 1
Упростить:
1) 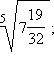
2) 
3) 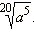
Решение (Приложение 1)
Пример 2
Упростите выражения 1) 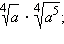 2)
2) 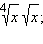 3)
3) 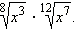
Решение (Приложение 1)
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!