

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Кафедра высшей математики
Лагунова М.В.
Конспект лекций
по
ТЕОРИИ ВЕРОЯТНОСТЕЙ
для студентов II курса
механико-машиностроительного факультета СПбГТУ
(часть I)

Санкт-Петербург 1997 г.
Глава I. Вероятностное пространство. Случайные события.
Элементы комбинаторики.
Комбинаторика - раздел элементарной математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. [Энциклопедический словарь юного математика].
Пусть B - конечное множество, состоящее из n различных элементов. Комбинаторика изучает вопрос о том, какого типа соединения можно составить из этих элементов и сколько таких соединений. Рассмотрим три основных типа соединений: перестановки, размещения и сочетания.
1. Перестановки из n элементов - всевозможные упорядоченные множества, составленные из данных n элементов.
Число перестановок из n элементов обозначается 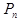 .
.
ПРИМЕР Пусть множество B состоит из трех цифр:  . Какие перестановки мы можем составить? Сколько их?
. Какие перестановки мы можем составить? Сколько их?
| 123 | 213 | 312 |
| 132 | 231 | 321 |
Две различные перестановки отличаются лишь порядком вхождения элементов множества B. Легко заметить, что 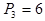 .
.
Помня о приведенном выше примере, выведем формулу для вычисления числа перестановок из n элементов.
Итак, элемент, стоящий на первом месте, можно выбрать из данных n элементов, очевидно, n способами. Если первый элемент уже выбран, то следующий за ним - второй - мы можем выбрать из оставшихся (n -1)- го элементов, естественно, (n -1)- м способом. А так как каждому выбору первого элемента перестановки соответствуют все возможные способы выбора второго элемента, для выбора первой пары элементов получим 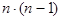 способ. Продолжая дальше в том же духе, получим:
способ. Продолжая дальше в том же духе, получим:
|
|
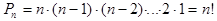
2. Размещения из n элементов по k - всевозможные упорядоченные k -элементные подмножества данного n -элементного множества.
Число размещений из n по k обозначается 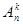 .
.
ПРИМЕР Множество 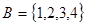 . Составим всевозможные размещения из 4-х элементов данного множества по 2.
. Составим всевозможные размещения из 4-х элементов данного множества по 2.
| 12 | 21 | 31 | 41 |
| 13 | 23 | 32 | 42 |
| 14 | 24 | 34 | 43 |
Как видно из приведенного примера, различные размещения могут отличаться как порядком входящих в них элементов так и самими элементами. Легко подсчитать, что 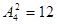 .
.
Выведем общую формулу для подсчета числа 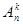 .
.
Имеется k порядочных мест, или разрядов, на которые мы должны поставить элементы, выбранные произвольно из данных n элементов. Эту процедуру удобно представить в виде таблицы:
| 1 | 2 | 3 | ... | k -2 | k -1 | k |
| n | n- 1 | n- 2 | ... | n-(k- 3) | n-(k- 2) | n -(k - 1) |
Здесь в первой строке обозначен порядковый номер входящего элемента, а в нижней - число способов, которыми мы этот элемент можем выбрать из оставшихся к данному моменту. При помощи рассуждений, которые мы приводили при выводе числа перестановок, получаем, что

3. Сочетания из n элементов по k - всевозможные k -элементные подмножества данного n -элементного множества.
 Число сочетаний из n по k обозначается
Число сочетаний из n по k обозначается 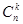 .
.
Сравните определения сочетаний и размещений.
ПРИМЕР Пусть по-прежнему множество 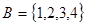 , выпишем всевозможные сочетания из этих 4-х элементов по 2:
, выпишем всевозможные сочетания из этих 4-х элементов по 2:
| 12 | 13 | 14 | 23 | 24 | 34 |
Два различных сочетания отличаются лишь входящими в них элементами, при этом легко подсчитать, что  . Таблица же для подсчета
. Таблица же для подсчета  содержит лишь одну строку.
содержит лишь одну строку.
Выведем общую формулу для подсчета числа сочетаний.
Ясно, что сочетаний из n элементов по k меньше, чем размещений из n элементов по k, ровно во столько раз, сколькими способами можно переставить эти k элементов, то есть 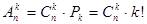 . Из этой формулы следует, что
. Из этой формулы следует, что
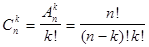
П Р И М Е Р Ы
|
|
При решении комбинаторных задач очень важно уметь определять типы соединений. Решим несколько задач.
1. Сколькими способами можно рассадить 8 человек на скамейку?
2. Сколькими способами можно рассадить 8 человек за круглый стол?
В первой задаче ответ очевиден. Речь идет о количестве перестановок из 8 элементов, т.е. 8 человек на скамейке можно пересаживать 8! различными способами.
Что касается второй задачи, то она отличается от предыдущей тем, что у круглого стола, как известно, нет краев. Представим себе, что мы выбрали одного конкретного человека и посадили его за стол, а далее начинаем различными способами пересаживать оставшиеся 7 человек. Сколькими способами это можно сделать? Да, конечно же, 7! способами.
3. Сколькими способами можно выбрать из группы в 12 человек 2-х студентов для участия в конференции?
4. Сколькими способами можно выбрать из группы в 12 человек старосту и его помощника?
В первом случае мы выбираем 2-х человек из 12, которые будут выполнять одинаковые обязанности - они просто вместе пойдут на конференцию. Число способов будет 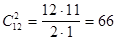 . Во втором случае выбираемые нами студенты будут выполнять разные функции, т.е. можно считать, что староста является в этой двойке лицом №1, а его заместитель - №2. Таким образом, речь идет об упорядоченном 2-х элементном подмножестве множества из 12 элементов, а таких подмножеств
. Во втором случае выбираемые нами студенты будут выполнять разные функции, т.е. можно считать, что староста является в этой двойке лицом №1, а его заместитель - №2. Таким образом, речь идет об упорядоченном 2-х элементном подмножестве множества из 12 элементов, а таких подмножеств 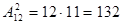 .
.
Рассмотрим пару более сложных задач.
5. Сколько словарей нужно создать, чтобы переводить с любого из 5-ти языков: хинди, болгарского, японского, суахили и чувашского непосредственно на любой другой из этих 5-ти языков?
Из условия задачи ясно, что нам понадобятся словари типа хинди - болгарского и болгарско - хинди и т.д. Обозначим хинди -болгарский словарь упорядоченной парой букв ХБ, а болгарско - хинди словарь - БХ. Таким же образом поступим с другими необходимыми нам словарями. Задача свелась к следующей: имеется множество, состоящее из 5 букв: {Х,Б,Я,С,Ч}. Сколько из них можно составить различных упорядоченных пар? Ответ: 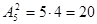 .
.
6. Сколькими способами можно прочесть слово A B R A C A D A B R A,
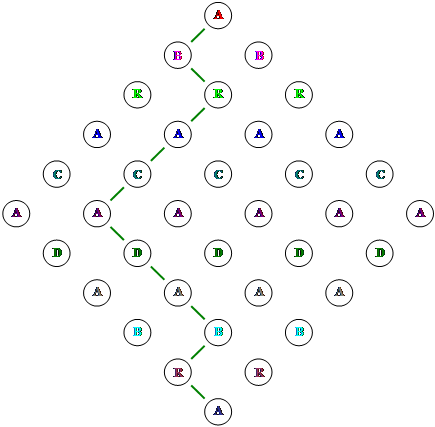 начиная c верхней буквы и кончая нижней. При этом каждая следующая буква должна находиться непосредственно под предыдущей (см. рисунок).
начиная c верхней буквы и кончая нижней. При этом каждая следующая буква должна находиться непосредственно под предыдущей (см. рисунок).
Один из возможных путей отмечен на рисунке. При этом, если каждый поворот направо обозначить буквой П, а каждый поворот налево - буквой Л, то получится, что пройденный путь можно записать при помощи этих букв следующим образом: ЛПЛЛЛПППЛП. Любой другой путь можно записать аналогичным образом. Легко заметить, что в каждой такой записи ровно 5 букв Л и 5 букв П. Причем по любому такому слову можно однозначно указать путь. Остается определить, сколько существует таких “слов”, или, по-другому, сколькими способами можно выбрать 5 мест из 10, на которые мы поставим букву Л, а остальные 5 мест займет, естественно, буква П. Ответ понятен - 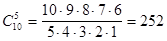 способа.
способа.
|
|
Свойства сочетаний.
Сочетания обладают рядом интересных свойств.
1. 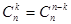
2. 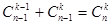
Эти свойства можно доказывать двумя способами: либо использовать формулу для подсчета числа сочетаний (предоставляем это читателю), либо при помощи здравого смысла.
Действительно, выбирая k элементов из n, мы просто делим множество на две части: те k элементов, которые мы взяли и n - k элементов, что мы оставили. Очевидно, что число способов взять или оставить одинаково 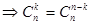 .
.
Чтобы доказать второе свойство сочетаний, зафиксируем один из элементов данного n -элементного множества. Заметим, что сочетания из k элементов бывают двух сортов: либо они содержат выбранный нами элемент (таких сочетаний 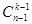 ), либо не содержат его (
), либо не содержат его (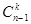 способов). Остается сложить эти две величины и получить общее число способов выбора из n элементов k.
способов). Остается сложить эти две величины и получить общее число способов выбора из n элементов k. 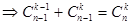 .
.
Из приведенных выше свойств следует знаменитый треугольник Паскаля.
3. Если числа сочетаний записать в виде треугольника в следующем виде:
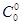
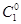
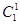
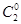
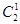
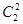
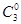
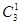
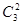
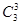
............
После подстановки численных значений получится:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
...............
По сторонам треугольника стоят единицы, а каждое число внутри треугольника является суммой двух чисел, стоящих непосредственно над ним.
4. Пользуясь числами сочетаний, выведем формулу бинома Ньютона 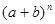 .
.
Вспомним формулу квадрата суммы: 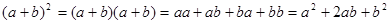
Рассуждая аналогичным образом для n -ой степени, (не переставляя сомножители!) получим сумму всевозможных слагаемых, каждое из которых представляет n -буквенное слово, составленное из букв a и b. При этом слагаемых, в которых k букв a и n - k букв b (вспомните пример с абракадаброй), ровно 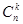 штук. А каждое такое слагаемое равно
штук. А каждое такое слагаемое равно 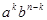 . Таким образом, получим:
. Таким образом, получим:
|
|
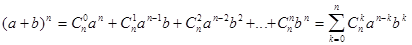 .
.
5. Пользуясь биномом Ньютона, приняв a = b = 1, получим
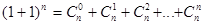 , т.е. число всех подмножеств
, т.е. число всех подмножеств
n -элементного множества равно 2n.
§2. Вероятностное пространство (W, A, P).
1. Пространство элементарных событий.
Def Пространство элементарных событий W - множество объектов произвольной природы.
Обычно в эксперименте множество W - множество взаимоисключающих исходов.
ПРИМЕРЫ:
1.

| Монета подбрасывается один раз. Элементарными исходами эксперимента являются 2 события: выпадение герба и выпадение решетки. (При описании элементарных исходов мы сразу оговариваем, что монета не может встать на ребро, зависнуть в воздухе или внезапно исчезнуть.) Таким образом, если обозначить элементарные исходы эксперимента w1 = Г - выпадение герба, w2 = Р - выпадение решетки, то пространство элементарных исходов является множеством, состоящим из двух элементов | ||
| 2. | Игральную кость подбрасывают один раз. Наблюдаемое событие - число выпавших очков. Элементарные исходы: w1 - выпало 1 очко, w2 - выпало 2 очка и т.д. w6 - выпало 6 очков. | ||
| 3. | Монета подбрасывается до первого появления герба. Элементарными исходами эксперимента являются события: w1= Г - герб появился при первом подбрасывании, w2 =РГ - герб появился при втором подбрасывании ,..., w k =РРР...РГ - герб появился при k -м подбрасывании ,... получим:
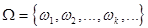 . В этом случае пространство элементарных исходов - бесконечное счетное множество. . В этом случае пространство элементарных исходов - бесконечное счетное множество.
| ||
4.

| Производится стрельба по плоской круглой мишени. Элементарные исходы - координаты точки попадания.
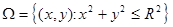 В этом случае пространство элементарных исходов - несчетное множество.
В этом случае пространство элементарных исходов - несчетное множество.
|
2. Алгебра событий A.
Def Случайным событием называется любое подмножество пространства элементарных событий W.
Обычно события обозначаются большими печатными латинскими буквами (кроме буквы P).
ПРИМЕР
Рассмотрим пример с подбрасыванием игральной кости. Как было показано ранее, пространство элементарных исходов 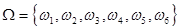
Событиями в данном эксперименте могут быть, например,
А - выпало четное число очков,
В - выпало число очков, кратное трем.
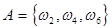 ,
, 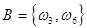 .
.
Используем этот пример при рассмотрении того, какие возможны
Операции над событиями
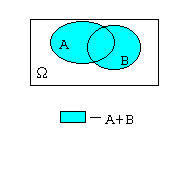
Суммой событий А и В называется множество, обозначаемое А+В=А 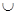 В и состоящее из элементов, входящих в А или В.
В приведенном выше примере
А+В = В и состоящее из элементов, входящих в А или В.
В приведенном выше примере
А+В = 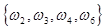 , это означает, что выпало либо четное число очков, либо число очков кратно трем. , это означает, что выпало либо четное число очков, либо число очков кратно трем.
| 
|
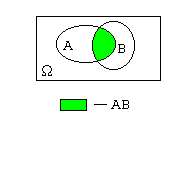
Произведением событий А и В называется множество, обозначаемое АВ=А 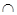 В и состоящее из элементов, входящих в А и В.
В приведенном выше примере
АВ = В и состоящее из элементов, входящих в А и В.
В приведенном выше примере
АВ = 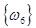 , это означает, что выпало четное число кратное трем. , это означает, что выпало четное число кратное трем.
| 
|
Разностью событий А и В называется множество, обозначаемое А\В и содержащее те элементы множества А, которые не входят в В.
В приведенном выше примере А\В = 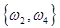 , что означает - выпало четное число очков не кратное трем. , что означает - выпало четное число очков не кратное трем.
| 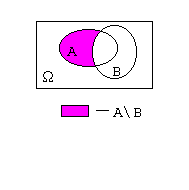 
|
Def Событие W называется достоверным.
|
|
Def Событие 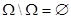 называется невозможным.
называется невозможным.
Def Событие 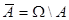 называется противоположным событию
называется противоположным событию 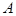 .
.
Def События А и В называются несовместными, если АВ =Æ.
Def Если A Ì B, то говорят, что событие A влечет событие В..
ПРИМЕРЫ
1. Событие А – “горит красный свет светофора” и событие В – “горит зеленый свет”, несовместны.
2. Событие А – “на игральной кости выпало два очка” влечет событие В – “выпало четное число очков”.
Свойства событий:
1. AA = A
2. A+A=A
3. A+ 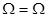
4. A 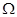 =A
=A
5. A 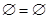
6. AB=BA
7. A+B=B+A
8. A(B+C)=AB+AC
9. (AB)C=A(BC)
10. (A+B)+C=A+(B+C)
11. 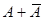
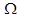
12. 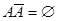
Эти свойства докажите самостоятельно.
Формулы де Моргана.
13. 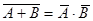
14. 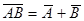
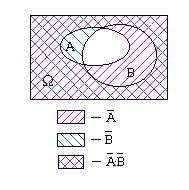
Докажем, например, предпоследнее свойство с помощью картинки, к которой часто прибегают в теории множеств.
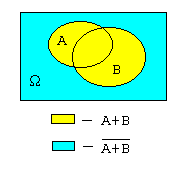
| 
|
Из картинок видно, что множества 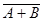 и
и 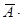
 состоят из одних и тех же элементов. (Можно провести и строгое доказательство, но мы не будем этого делать, т.к. оно абсолютно не наглядно.)
состоят из одних и тех же элементов. (Можно провести и строгое доказательство, но мы не будем этого делать, т.к. оно абсолютно не наглядно.)
NOTE: Понятия произведения и суммы событий переносятся на бесконечную последовательность событий.
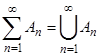
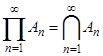
Def Пусть W - пространство элементарных событий. A - некоторый класс подмножеств множества W. A - алгебра событий, если " A, B Î A
1. W Î A
2. AB Î A
3. A+B Î A
4. A – B Î A
NOTE: Из свойств 1 и 4 следует, что 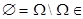 A.
A.
ПРИМЕРЫ
1. A= 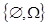
2. A= 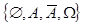 , где
, где 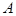 - некоторое событие.
- некоторое событие.
3. Система всех подмножеств множества W также является алгеброй событий.
ПРИМЕР Вспомним эксперимент с подбрасыванием игральной кости. 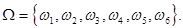 Пусть алгебра событий A - система всех подмножеств множества W.
Пусть алгебра событий A - система всех подмножеств множества W.
A = 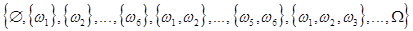
Сколько элементов в множестве A?
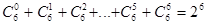
Таким образом, если множество W конечно, то и алгебра A конечна.
3. Вероятность события P.
Def Числовая функция P (А), заданная на классе событий A, называется вероятностью, если выполнены следующие аксиомы:
A-1 A - алгебра событий.
А-2 " A Î A P(A) ³ 0
A-3 P (W)= 1
A-4 (аксиома конечной аддитивности) Если события А и В несовместны, т.е. AB = Æ, то P (A + B)= P (A)+ P (B).
Def Тройка (W, A, P), где W - пространство элементарных событий, A - алгебра событий, а P - определенная на этой алгебре вероятность, называется вероятностным пространством.
Свойства вероятности:
1. 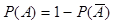
2. 
3. 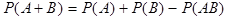 - формула вероятности суммы
- формула вероятности суммы
4. 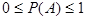
5. 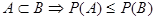
Доказательство:
1. Т.к. 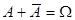 ,
, 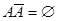 , то по аксиоме А-4 имеем:
, то по аксиоме А-4 имеем:
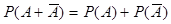 ,
, 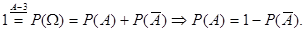
2. 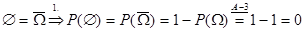
3. Если А и В несовместны, то формула вероятности суммы событий следует из аксиомы конечной аддитивности. Пусть А и В совместны.
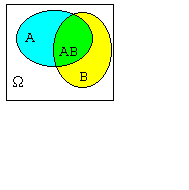
| 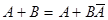 , причем события , причем события 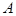 и и 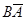 несовместны. несовместны.
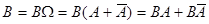 , причем события , причем события 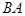 и и 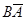 также являются несовместными. Пользуясь два раза аксиомой конечной аддитивности, получим: также являются несовместными. Пользуясь два раза аксиомой конечной аддитивности, получим:
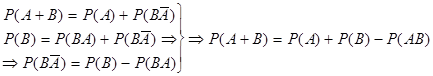
|
4. Докажем, что 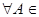 A
A 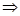
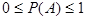 . По аксиоме А-2 мы знаем, что
. По аксиоме А-2 мы знаем, что 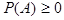 ,а так как
,а так как 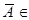 A, значит и
A, значит и 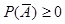 . По свойству 1.
. По свойству 1. 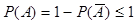 .
.
5.
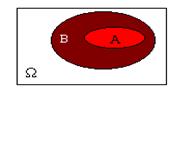
| Покажем, что 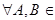 A: A: 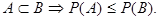 Имеем: Имеем: 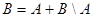 , причем события , причем события 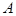 и и 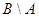 несовместны. Тогда по аксиоме конечной аддитивности несовместны. Тогда по аксиоме конечной аддитивности 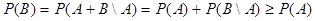 .
Q.E.D. .
Q.E.D.
|
NOTE: Для суммы трех произвольных событий можно доказать следующую формулу:
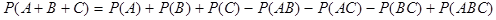 . Докажите эту формулу самостоятельно, а также обобщите теорему о вероятности суммы событий на случай произвольного конечного числа событий.
. Докажите эту формулу самостоятельно, а также обобщите теорему о вероятности суммы событий на случай произвольного конечного числа событий.
Геометрические вероятности.
Классическое определение вероятности нельзя применить, если пространство элементарных событий W, бесконечно.
Пусть W - замыкание непустой ограниченной области с кусочно-гладкой границей на плоскости или в пространстве. Тогда, как мы знаем, существует ненулевая мера Жордана области W (площадь, если W плоская область и объем, если W - область в пространстве). Меру Жордана в обоих случаях будем обозначать, как и прежде, mW.
Пусть A- система подмножеств W, имеющих кусочно-гладкую границу. Проверьте самостоятельно, что A- алгебра.
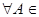 A положим
A положим
| (1) | 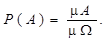 
|
Проверьте самостоятельно, что определенная этой формулой вероятность удовлетворяет требуемым аксиомам.
NOTE: Множества, имеющие нулевую меру Жордана, будем так же как и Æ называть невозможными событиями. К ним относятся точки и кусочно-гладкие кривые. Вообще говоря, невозможное событие можно определить как событие, вероятность которого равна нулю.
ПРИМЕРЫ
1.
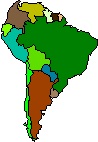
| Известно, что площадь Южной Америки составляет 17,8 млн. кв. км. Площадь Бразилии - 8,5 млн. кв. км. Случайным образом выбирается точка на карте Южной Америки. Какова вероятность того, что она попала на карту Бразилии (событие А)?
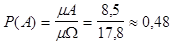
|
2. Задача о встрече

| Два студента, назовем их Иван и Петр, договорились о встрече в интервале от 0 до 1 часа дня. Каждый из них приходит в любой момент названного интервала времени, ждет не более 15 минут и уходит, если не дождется другого. Найти вероятность того, что встреча состоится. |
Пусть событие А - встреча состоялась. Найдем P (А).
Введем две величины:
х - время прихода Ивана;
у - время прихода Петра.
Тогда пространство элементарных событий 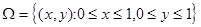 .
.
Посмотрим, при каких значениях х и у встреча состоится. Возможны два варианта:
а) Иван пришел первым, т.е. 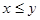 , тогда встреча состоится, если
, тогда встреча состоится, если 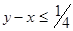 ;
;
б) Петр пришел первым, т.е. 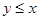 , в этом случае встреча состоится, если
, в этом случае встреча состоится, если 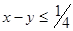 .
.
В любом случае
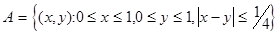 .
.
Изобразим на чертеже плоскую область W, множество А, а также найдем отношение их площадей.
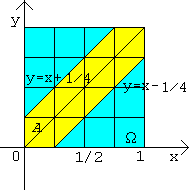
Из рисунка видно, что m W=1, а 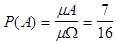 .
.
Условные вероятности.
ПРИМЕР
Студент из 30 билетов выучил 1 - 3 и 28 -30. На экзамен он вошел 11-м. К этому моменту остались билеты 1 - 20. Найти вероятность того, что студент вытащит тот билет, который выучил.
Пусть событие В - студент получил билет, который выучил,
А - остались билеты 1 - 20. Пространство элементарных событий 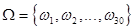 , где элементарный исход
, где элементарный исход  означает, что студент вытащил i -й билет. Тогда
означает, что студент вытащил i -й билет. Тогда 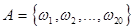 ,
, 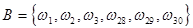 . Если мы не знаем, что произошло событие А, то
. Если мы не знаем, что произошло событие А, то
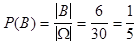 ,при дополнительной информации - произошло событие А - пространство элементарных исходов сужается до множества А.
,при дополнительной информации - произошло событие А - пространство элементарных исходов сужается до множества А.
ВА - событие, состоящее в том, что события А и В наступают одновременно, т.е. студент вытащил билет, который знает, из 20-ти оставшихся.
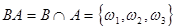 ,
, 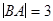 .
.
Обозначим 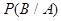 - вероятность события В при условии, что событие А произошло. В нашем примере ясно, что
- вероятность события В при условии, что событие А произошло. В нашем примере ясно, что 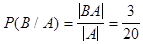 , а т.к.
, а т.к. 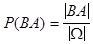 и
и 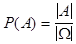 , можно проверить, что
, можно проверить, что 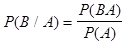 .
.
Def Пусть (W, A, P) - произвольное вероятностное пространство. События A, B Î A, причем P (A) >0. Условной вероятностью события В при условии, что событие А произошло, называется величина, обозначаемая
P (B / A)= P (AB): P (A).
NOTE: Пусть зафиксировано событие А Î A, причем P (A) >0. Обозначим 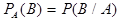 . Можно проверить, что условная вероятность
. Можно проверить, что условная вероятность 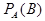 удовлетворяет всем аксиомам вероятности, а следовательно для нее справедливы и все свойства вероятности.
удовлетворяет всем аксиомам вероятности, а следовательно для нее справедливы и все свойства вероятности.
Def События А и В называются независимыми, если
P (АВ)= P (А) P (В).
NOTE: Условие независимости двух событий можно записать, используя определение условной вероятности, в следующей форме: А, В независимы 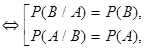
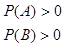 .
.
Это просто означает, что вероятность появления события А (или В) не зависит от того, осуществилось событие В (или А) или нет.
§6. Вероятность произведения n событий. Попарная независимость и независимость в совокупности.
Для произведения двух событий формула вероятности произведения имеет вид:
| (1) | 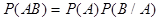
|
Для произведения n событий докажем следующую теорему:
Т_ 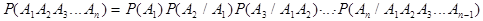
Здесь 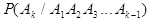 - вероятность того, что произошло событие
- вероятность того, что произошло событие 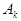 при условии, что уже осуществились все события
при условии, что уже осуществились все события 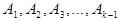 .
.
Доказательство: Воспользуемся методом математической индукции.
1) База для индукции. Пусть n =2. Тогда 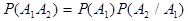 - известная формула.
- известная формула.
2) Индукционное предположение. Пусть формула верна при n = k.
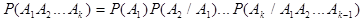
3). Индукционный переход. Докажем, что тогда формула верна и для n = k + 1. 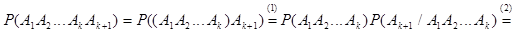
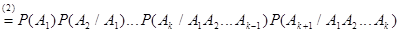 .
.
Таким образом, мы показали наличие базы для индукции и доказали законность индукционного перехода.
Q. E. D.
ПРИМЕР:
В урне находятся 15 белых и 10 черных шаров. Наудачу извлекаются 7 шаров. Какова вероятность того, что все они черные?
Пусть событие А - все шары черные.
Конечно, эту задачу можно решить по-старому, используя классическое определение вероятности:
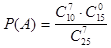 .
.
Используем формулу вероятности произведения событий. Представим себе, что мы вытаскиваем шары по одному. Событие 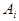 - i -й вынутый шар черный. Очевидно,
- i -й вынутый шар черный. Очевидно, 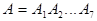 . Воспользуемся формулой вероятности произведения:
. Воспользуемся формулой вероятности произведения:
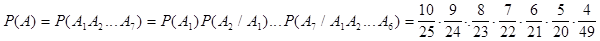
Проверьте, что результаты совпадут.
Def События А1, А2,..., А n называются попарно независимыми, если
P (AiAj)= P (Ai) P (Aj) при " i ¹ j.
Def События А1, А2,..., А n называются независимыми в совокупности, если
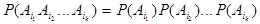
для любых комбинаций индексов 1 £ i 1 < i 2 <...< ik £ n.
NOTE: Очевидно, что из независимости в совокупности следует попарная независимость. Обратное утверждение, как показывает приведенный ниже пример, не является верным.
ПРИМЕР Бертрана: Приведем пример попарно независимых, но не являющихся независимыми в совокупности событий.
Пусть имеется правильный тетраэдр, раскрашенный следующим образом: три его грани однотонные и окрашены соответственно в красный, синий и зеленый цвета, а последняя грань раскрашена тремя этими цветами (см. рис.)
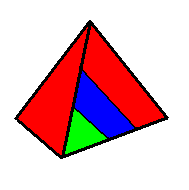
| Один раз подбрасываем этот тетраэдр. Считается, что он с равной вероятностью может упасть любой гранью вниз. Введем в рассмотрение три события:
R - на нижней грани есть красный цвет,
G - на нижней грани есть зеленый цвет,
B - на нижней грани есть синий цвет.
Очевидно, что 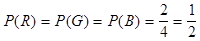 . .
|
Событие RB, например, означает, что на нижней грани есть одновременно красный и синий цвет, т.е. тетраэдр упал трехцветной гранью вниз. Точно также мы можем рассматривать события RG, BG и RGB. Причем все они означают одно и то же, а именно, что тетраэдр упал трехцветной гранью вниз. Найдем вероятности всех перечисленных выше событий.
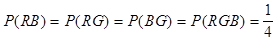 .
.
Нетрудно проверить, что 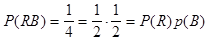 . Аналогично проверяется, что
. Аналогично проверяется, что 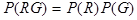 и
и 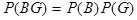 .
.
Таким образом, мы показали, что события R, G и B попарно независимы. Если бы они были независимыми в совокупности, то должно было бы выполняться и еще одно равенство:
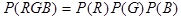 , а оно не выполняется, т.к.
, а оно не выполняется, т.к. 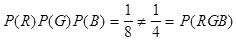 .
.
_Т_ Если события 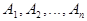 независимы в совокупности, то
независимы в совокупности, то 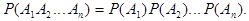
Эта теорема не нуждается в доказательстве, потому что это прямое следствие определения независимых в совокупности событий.
Формула полной вероятности.
ПРИМЕР:
Рассмотрим пример на интуицию.
  № 1 № 2
№ 1 № 2
| Пусть имеются две коробки, а также 10 купюр по DM 10 и столько же купюр по DM 20. Некто подходит к любой из коробок и вытягивает одну купюру. Как следует разложить купюры, чтобы с наибольшей вероятностью попалась бы купюра в DM 20? | 

|
Возможные варианты ответа (собранные за многолетнюю практику работы со студентами) запишем в виде таблицы:
| коробка № 1 | коробка № 2 |

| 
| 
| 
|
| 5 | 5 | 5 | 5 |
| 0 | 10 | 10 | 0 |
| 10 | 10 | 0 | 0 |
| 0 | 1 | 10 | 9 |
Как нам подсказывает интуиция, последний способ, по-видимому, является самым подходящим. Вернемся к теории (вероятностей).
_Т_ Пусть событие 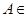 A, события
A, события 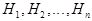 такие, что
такие, что
1) 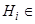 A
A 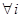 ,
,
2) 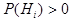
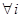 ,
,
3) 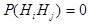 при любых
при любых 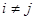 ,
,
4) 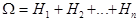 ;
;
Тогда полная вероятность события 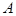 вычисляется по формуле:
вычисляется по формуле:
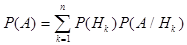 .
.
Def Система множеств { Hi }, удовлетворяющая условиям 1) - 4), называется полной группой событий, каждое из событий Hi называется гипотезой.
NOTE: Вместо условия 4) достаточно потребовать, чтобы 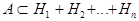 .
.
Доказательство: Разобьем пространство элементарных исходов W на множества 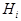 так, как указано в условии теоремы.
так, как указано в условии теоремы.
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!