Общее решение линейного однородного дифференциального уравнения второго порядка.

Теорема Коши

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

       Если функция (n +1) переменных вида в некоторой области D (n +1)- мерного пространства непрерывна и имеет непрерывные частные производные по , то какова бы не была точка ( 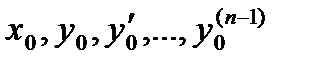) в этой области, существует единственное решение  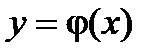 уравнения 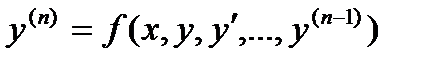, определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

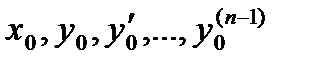Определитель Вронского

       Теорема. Если функции 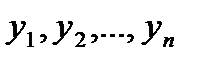 линейно зависимы, то составленный для них определитель Вронского равен нулю.

 

       Теорема. Если функции 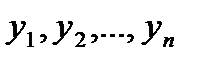линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.

 

       Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения 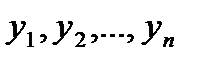 была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.

       Теорема. Если 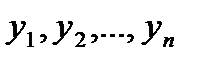 - фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.

,

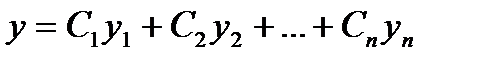где C_i – постоянные коэффициенты.

Общее решение линейного однородного дифференциального уравнения второго порядка.

         Теорема. Если задано уравнение вида  и известно одно ненулевое решение у = у₁, то общее решение может быть найдено по формуле:

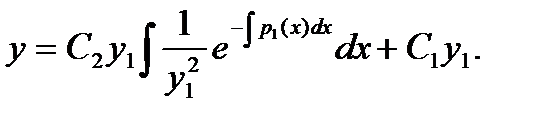
       Таким образом, для получения общего решения надо подобрать какое – либо частное решение дифференциального уравнения, хотя это бывает часто довольно сложно.

Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.

           Теорема. Общее решение линейного неоднородного дифференциального уравнения в некоторой области есть сумма любого его решения и общего решения, соответствующего линейного однородного дифференциального уравнения.

Свойства Рядов.

2) Рассмотрим два ряда 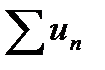 и 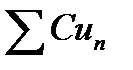, где С – постоянное число.

       Теорема. Если ряд 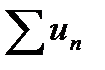сходится и его сумма равна S, то ряд 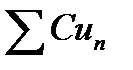тоже сходится, и его сумма равна С S. (C ¹ 0)

3) Рассмотрим два ряда 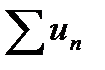и 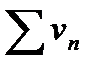. Суммой или разностью этих рядов будет называться ряд 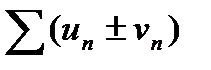, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.

       Теорема. Если ряды 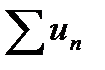и сходятся и их суммы равны соответственно S и s, то ряд 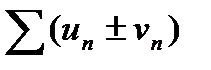 тоже сходится и его сумма равна S + s.

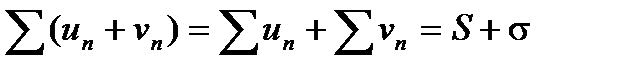
Разность двух сходящихся рядов также будет сходящимся рядом.

Сумма сходящегося и расходящегося рядов будет расходящимся рядом.

О сумме двух расходящихся рядов общего утверждения сделать нельзя.

6. Критерий Коши (необходимые и достаточные условия сходимости ряда).

Для того, чтобы последовательность 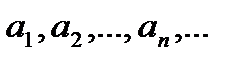была сходящейся, необходимо и достаточно, чтобы для любого  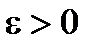существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:

.

 

       Доказательство. (необходимость)

Пусть 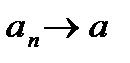, тогда для любого числа 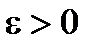найдется номер N такой, что неравенство

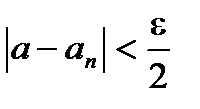 выполняется при n>N. При n>N и любом целом p>0 выполняется также неравенство 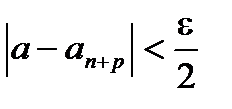. Учитывая оба неравенства, получаем:

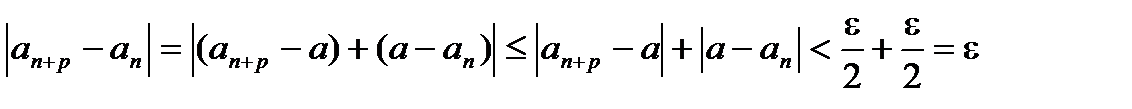
Необходимость доказана. Доказательство достаточности рассматривать не будем.

Сформулируем критерий Коши для ряда.

 

       Для того, чтобы ряд 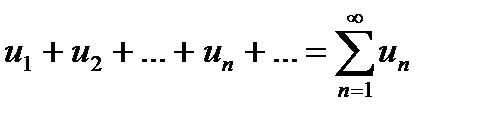был сходящимся необходимо и достаточно, чтобы для любого  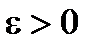существовал номер N такой, что при n > N и любом p >0 выполнялось бы неравенство

.

 

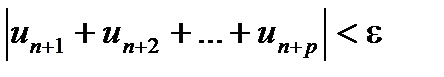       Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому как правило используются более простые признаки сходимости:

 

       1) Если ряд 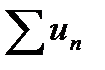сходится, то необходимо, чтобы общий член u_n стремился к нулю. Однако, это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд  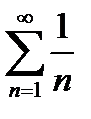является расходящимся, хотя его общий член и стремится к нулю.

 

       Пример. Исследовать сходимость ряда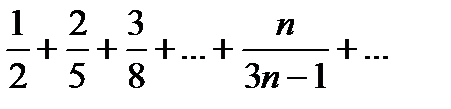

Найдем 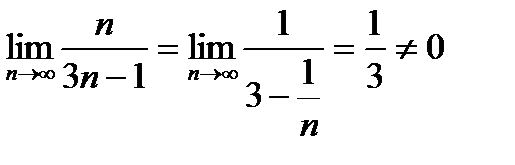 - необходимый признак сходимости не выполняется, значит ряд расходится.

 

       2) Если ряд сходится, то последовательность его частных сумм ограничена.

Однако, этот признак также не является достаточным.

Например, ряд 1-1+1-1+1-1+ … +(-1)ⁿ⁺¹+… расходится, т.к. расходится последовательность его частных сумм в силу того, что

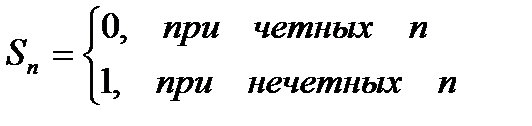
       Однако, при этом последовательность частных сумм ограничена, т.к. 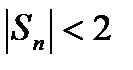 при любом n.

Теоремы Абеля.

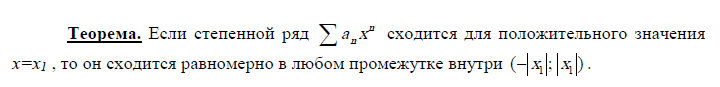
Несобственный интеграл.

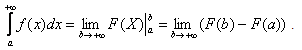
Теорема о среднем значении.

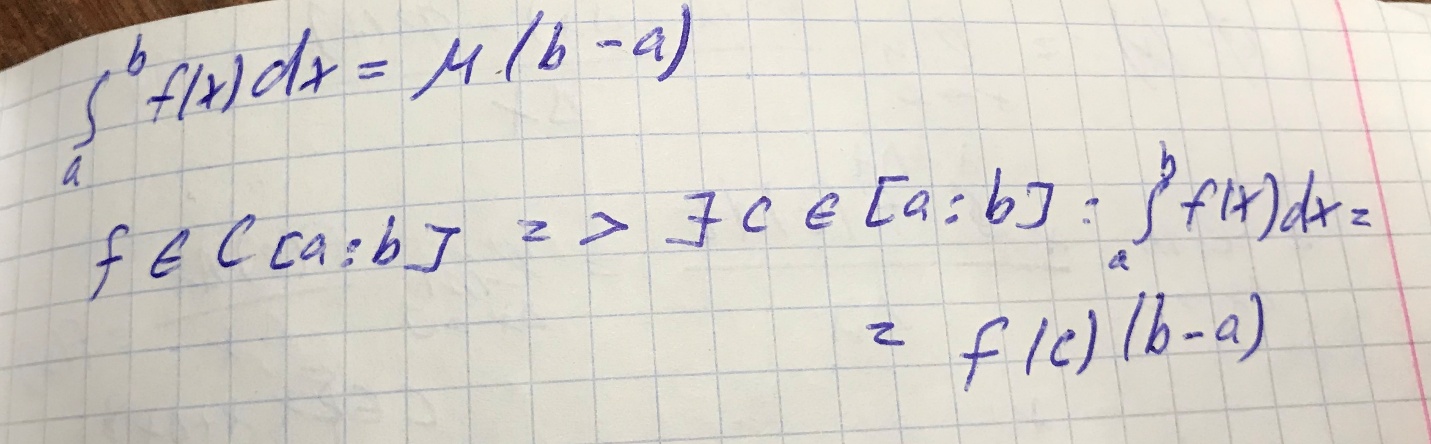
Теорема Коши

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

       Если функция (n +1) переменных вида в некоторой области D (n +1)- мерного пространства непрерывна и имеет непрерывные частные производные по , то какова бы не была точка ( 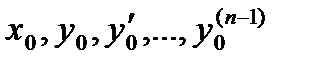) в этой области, существует единственное решение  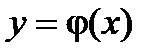 уравнения 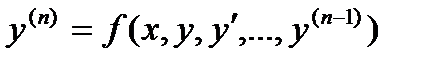, определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

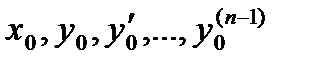Определитель Вронского

       Теорема. Если функции 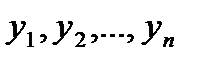 линейно зависимы, то составленный для них определитель Вронского равен нулю.

 

       Теорема. Если функции 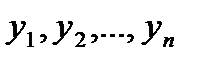линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.

 

       Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения 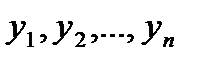 была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.

       Теорема. Если 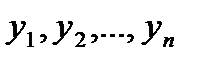 - фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.

,

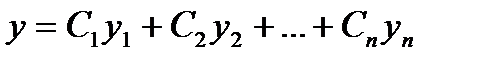где C_i – постоянные коэффициенты.

Общее решение линейного однородного дифференциального уравнения второго порядка.

         Теорема. Если задано уравнение вида  и известно одно ненулевое решение у = у₁, то общее решение может быть найдено по формуле:

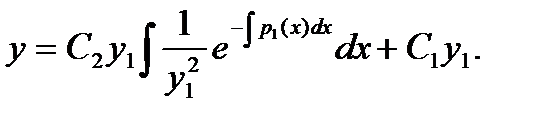
       Таким образом, для получения общего решения надо подобрать какое – либо частное решение дифференциального уравнения, хотя это бывает часто довольно сложно.