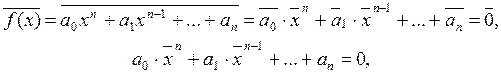Определение 1. Множество F, содержащее не менее двух элементов, называется полем, если на множестве F определены две бинарные алгебраические операции, называемые сложением и умножением, которые каждой паре элементов a, b Î G ставит в соответствие единственные элементы из G, обозначаемый соответственно a + b и ab, и выполняются условия:
1) (F, +) - аддитивная абелева группа;
2) (F \ {0}, ×) – мультипликативная абелева группа;
3) 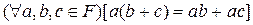 - дистрибутивный закон.
- дистрибутивный закон.
Далее везде обозначаем F * = F \ {0} и называем мультипликативной группой поля.
Определение 2. Подмножество P поля F, содержащее не менее двух элементов, называем подполелем поля F, если выполняются условия:
1) 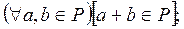
2) 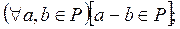
3) 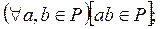
4) 
Легко доказать, что каждое подполе P поля F само является полем относительно операций, определенных в поле F.
Определение 3. Если P подполе поля F, то F называется расширением поля P и обозначается через F / P.
Если F - расширение поля P, то F является линейным пространством над полем P. Если F является конечномерным линейным пространством над полем P, то расширение F / P называется конечным, а размерность n пространства F над полем P называется степенью расширения F / P и обозначается символом n = [ F: P ]. По определению размерности это обозначает, что в поле F существует базис (w1, w2, …, w n), что любой элемент aÎ F единственным образом представляется в виде:
a = a 1w1 + a 2w2 + …+ an w n; a 1, a 2, …, an Î P. (1)
Элементы w1, w2, …, w n называются базисом расширения F / P.
Из этого определения легко вытекает следующая теорема.
Теорема 1. Если F / P, H / F конечные расширения, то
[ H: P ] = [ H: P ] [ F: P ].ÿ
Определение 4. Пусть F подполе поля H, q Î H. Минимальное (по включению) поле, содержащее поле F и элемент q называется простым расширением поля F, полученным присоединением к полю F элемента q.
Обозначается простое расширение поля F, полученным присоединением к полю F элемента q через F (q).
Определение 5. Пусть F - подполе поля H, f (x) – многочлен с коэффициентами из поля F; q - корень многочлена f (x) в поле H. Тогда простое расширение F (q) называется простым алгебраическим расширением поля F, полученным присоединением к полю F корня q многочлена f (x). Если f (x) – неприводимый многочлен степени n над полем F, то расширение F (q) называется простым алгебраическим расширением поля F степени n.
Теорема 2. Пусть F подполе поля H, f (x) – неприводимый многочлен степени n над полем F, q - корень многочлена f (x) в поле H. Тогда любой a элемент поля F (q) единственным образом представляется в виде:
a = a 0 + a 1q + a 2q2 + …+ an- 1q n- 1; a 0, a 1, …, an- 1 Î F. (2) .
Доказательство. Докажем сначала единственность представления элемента a в виде (2). Допустим противное, что для некоторого элемента a Î F (q) имеется кроме (2) еще другое представление
a = b 0 + b 1q + b 2q2 + …+ bn- 1q n- 1; b 0, b 1, …, bn- 1 Î F. (3)
Вычитая почленно из равенства (2) равенство (3) получим равенство
(a 0 - b 0) + (a 1 – b 1)q + (a 2 – b 2)q2 + …+ (an- 1 – b n- 1)q n- 1 = 0.
Из этого следует, что неприводимый над F многочлен f (x) и многочлен
(a 0 - b 0) + (a 1 – b 1) x + (a 2 – b 2) x 2 + …+ (an- 1 – b n- 1) x n- 1
степени меньшей n имеют общий корень q. Тогда последний многочлен делится на f (x) и поэтому тождественно равен нулю. Отсюда a 0 = b 0, a 1 = b 1, …, an - 1 = b n - 1. Получили противоречие с предположением.
Обозначим через M (q) множество всех элементов вида (2). Так как F (q) - минимальное поле, включающее поле F и элемент q, то M (q)Í F (q). Докажем обратное включение.
Докажем, что M (q) подполе поля H. Легко проверить, что сумма, разность, произведение элементов вида (2) имеет тот же самый вид. Докажем, что обратный элемент для элемента a¹0 вида (2) имеет тот же вид. Пусть имеет вид (2). Тогда a= g (q), где g (x) – многочлен с коэффициентами из F степени меньшей n. Тогда многочлены g (x) и f (x) – взаимно простые. Следовательно, существуют такие многочлены u (x), v (x) Î F [ x ], степень u (x) < n, что выполняется равенство:
u (x) g (x) + v (x) f (x)= 1.
Полагая в этом равенстве x = q получим u (q) g (q) + v (q) f (q)= 1. Так как f (q) = 0, g (q) = a, то получим u (q) a = 1. Отсюда элемент u (q)Î M (q), обратный для a.
Таким образом, M (q) – подполе поля H. Отсюда M (q) – поле, включающее поле F и элемент q. Так как F (q) - минимальное поле с таким свойством, то F (q)Í M (q).
Отсюда и из доказанного выше включения следует F (q) = M (q). ÿ
Следствие. Простое алгебраическое расширение поля F степени n является конечным расширением поля F степени n и с базисом
1, q, q2, …,q n - 1.
Определение 6. Пусть F поле H, f (x) – многочлен с коэффициентами из поля F. Полем разложения многочлена f (x) называется минимальное расширение H поля F, в котором многочлен f (x) разлагается в произведение линейных над полем H многочленов.
Теорема 3. Пусть F - поле, f (x) – многочлен над полем F. Тогда
1) существует поле разложения многочлена f (x);
2) любые два поля разложения многочлена f (x) изоморфны.
Доказательство. 1. Существование. Доказываем теорему для случая, когда f (x) – многочлен неприводимый над полем F. Общий случай сводится к этому построением цепочки расширений указанного вида. Итак, пусть многочлен f (x) – неприводимый над полем F многочлен степени n.
Рассмотрим кольцо H классов вычетовкольца многочленов F [ x ]по модулю идеала (f), порожденным многочленом f = f (x): H = F [ x ]/(f).
Кольцо H состоит из классов вычетов вида` g = { h = g + f u | u Î F [ x ]}, где g – некоторый фиксированный многочлен из F [ x ], в частности g может быть элемент поля F. В качестве многочленов g можно рассматривать все многочлены из F [ x ] равные нулю или степени не выше n.
Классы вычетов вычитаются и умножаются по правилам 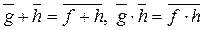 ,
,
нулевым и единичными классоми является соответственно классы `0 и `1, противоположным классом для класса ` g является класс 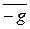 . Покажем, что для каждого класса ` g ¹`0 существует обратный класс. Так как ` g ¹`0, то многочлен g не делится на f, а так как многочлен f неприводимый над полем F, то многочлены f и g взаимно простые.Следовательно, существуют такие многочлены u, v Î F [ x ], что выполняется равенство fu + gv = 1. Переходяк классам получаем
. Покажем, что для каждого класса ` g ¹`0 существует обратный класс. Так как ` g ¹`0, то многочлен g не делится на f, а так как многочлен f неприводимый над полем F, то многочлены f и g взаимно простые.Следовательно, существуют такие многочлены u, v Î F [ x ], что выполняется равенство fu + gv = 1. Переходяк классам получаем 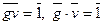 . Поэтому для класса ` g существует в H обратный класс ` v. Легко проверяется, что операции сложения, умножения классов однозначны и для них выполняются все свойства поля. Таким образом, множество классов вычетов H по модулю многочлена f является полем.
. Поэтому для класса ` g существует в H обратный класс ` v. Легко проверяется, что операции сложения, умножения классов однозначны и для них выполняются все свойства поля. Таким образом, множество классов вычетов H по модулю многочлена f является полем.
Поле содержит поле изоморфное полю F. Каждому элементу a Î F можно единственным образом сопоставить класс ` a Î H. Легко проверить, что такое соответствие взаимно однозначное и сохраняет операции: для любых a, b Î F
 ,
,
т.е. является изоморфным вложением поля F в поле H. Таким образом, можно считать, что поле H является расширением поля F и для элементов a Î F считать, что 
Покажем, что многочлен в поле H имеет корень. Пусть
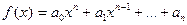 .
.
Так как f | f, то класс ` f =`0. Поэтому
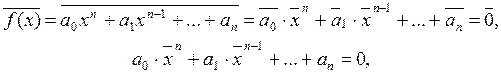
и класс ` x Î H является корнем многочлена f.
Тогда по теореме Безу многочлен f можно представить в виде
f (x) = (x -` x) f 1(x); x -` x, f 1(x) Î Н [ x ].
Если необходимо, повторяя рассуждения с многочленом f 1(x) мы найдем такое расширение поля F, в котором многочлен разлагается на линейные множители.
Можно доказать, что все поля разложения многочлена f изоморфны.ÿ



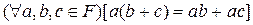 - дистрибутивный закон.
- дистрибутивный закон.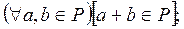
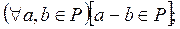
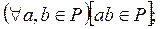

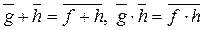 ,
,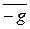 . Покажем, что для каждого класса ` g ¹`0 существует обратный класс. Так как ` g ¹`0, то многочлен g не делится на f, а так как многочлен f неприводимый над полем F, то многочлены f и g взаимно простые.Следовательно, существуют такие многочлены u, v Î F [ x ], что выполняется равенство fu + gv = 1. Переходяк классам получаем
. Покажем, что для каждого класса ` g ¹`0 существует обратный класс. Так как ` g ¹`0, то многочлен g не делится на f, а так как многочлен f неприводимый над полем F, то многочлены f и g взаимно простые.Следовательно, существуют такие многочлены u, v Î F [ x ], что выполняется равенство fu + gv = 1. Переходяк классам получаем 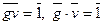 . Поэтому для класса ` g существует в H обратный класс ` v. Легко проверяется, что операции сложения, умножения классов однозначны и для них выполняются все свойства поля. Таким образом, множество классов вычетов H по модулю многочлена f является полем.
. Поэтому для класса ` g существует в H обратный класс ` v. Легко проверяется, что операции сложения, умножения классов однозначны и для них выполняются все свойства поля. Таким образом, множество классов вычетов H по модулю многочлена f является полем. ,
,
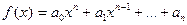 .
.