Представление целого числа в g -ичной системе счисления

Теорема 1. Пусть g – целое число> 1, S = {0, 1, …, g -1}. Тогда любое целое число a > 1 единственным образом представляется в виде

,                               (1)

где a_i Î S, i = 1,…, n.

Доказательство. Существование представления (1) доказываем методом математической индукции по a. Пусть a = 1. Тогда формула (1) имеет место при n =0, a ₀ = 1.

Предположим, что равенство (1) имеет место для любого целого числа q, 1£ q < a и докажем его для числа a. Разделим число a на g с остатком:

a = gq + r, 0£ r < g.                                         (2)

Если q = 0, то равенство (1) имеет место при    n =0, a ₁ = r. Если q >0, то

a = gq + r ³ gq > q

и к числу q можно применить индуктивное предположение. По индуктивному предположению:

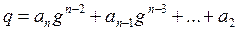,                             (3)

где a_i Î S, i = 2,…, n. Подставляя (3) в (2) получим

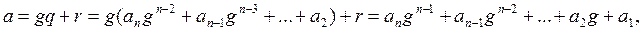
где a ₀ = r, a_i Î S, i = 0,…, n. Существование представления (1) доказано.

Доказывая единственность, допустим противное, что существует такое число для которого имеется два представления. Пусть a – наименьшее натуральное число для которого имеется два представления (1) и

  ,                               (4)

где b_i Î S, i = 1,…, m. Тогда имеем

,

 

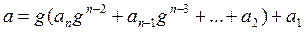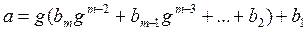
где a ₁, b ₁Î S. В силу теоремы о делении с остатком получим:

a ₁ = b ₁, .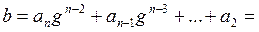

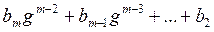Так a – наименьшее натуральное число, для которого имеется два разложения вида (1), то для числа b < a имеет место одно разложение вида (1). Тогда получим, что m = n и a ₁ = b ₁, a ₂ = b ₂, a ₃ = b ₃, ….. Получаем противоречие с предположением и единственность доказана.ÿ

Представление целого числа a в виде (1) называется g – ичным представлением целого числа. При этом число g называется основанием системы счисления, числа множества S = {0, 1, …, g -1} будем называть цифрами g – ичной системы счисления. Число n называется значностью числа a. Сокращенно равенство (1) записывают в виде:

 

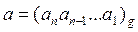
или в виде массива

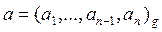,                                          (5)

при этом в массиве допускаются последние нулевые элементы.

Перевод числа a из g ₁ – ичной записи в g – ичную производится деление числа a на g с остатком, полученный остаток число a ₀,  а неполное частное q ₁; q ₁ делим на g с остатком, полученный остаток число a ₁,  а неполное частное q ₂; q ₂ делим на g с остатком, полученный остаток число a ₂,  а неполное частное q ₃; и т.д.

 

3. Целочисленная арифметика многократной точности

 

Будем считать, что основание не всегда равно 2, можно предполагать, что оно имеет размер машинного слова или двойного слова. Будем считать, что данные числа записаны в g – ичной системе счисления в виде массива (5), каждая цифра числа записана в отдельную ячейку памяти. При этом предполагаем, что натурально число записано не более n g – ичными цифрами. Последние цифры допускаются равными нулю. Знак целого числа удобно хранить в отдельной ячейке. Предполагаем, что программа реализуется на ассемблере, где реализована программа деления с остатком за один шаг. Обозначаем такое деление в виде:

(q, r)=div(a, b),

где q и   r  соответственно неполное частное и остаток от деления a на b.

Пусть даны два целых числа

,

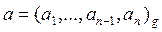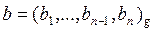
Знак переноса в другой разряд обозначаем через f (флаг переноса).

Алгоритм сложения неотрицательных целых чисел:

Вход: , ;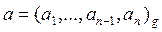

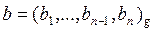f:=0;

for i = 1… n; (f, c_i): = div (a_i + b_i + f, g); end for

if f > 0 then n:= n +1; c_n:= f; end if

Выход: .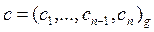

При сложении двух n -значных чисел требуется выполнить   n операций деления с остатком и 2 n операций сложений чисел величиной с цифру.

При вычитании сначала проверяется, находится знак разности, а затем из числа с большим модулем вычитается число с меньшим модулем. Предполагается, что знак разности сохраняется в ячейке c ₀.

Алгоритм вычитания неотрицательных целых чисел:

Вход: , ;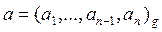

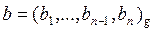c = 0; f:=0;

for i = n …1; if a_i > b_i then c ₀:=+1; break  else if a_i < b_i then c ₀:= -1; break  end if;

End for

if c ₀:= 1 then

for i = 1… n; (f, c_i): = div (a_i - b_i + f, g); end for

else if c ₀:= -1 then

for i = 1… n; (f, c_i): = div (b_i - a_i + f, g); end for

end if;

Выход: .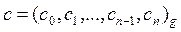

При вычитании двух n -значных чисел требуется выполнить   n операций деления с остатком и 2 n операций вычитаний чисел величиной с цифру и n сравнений.

Пусть даны два целых числа

,

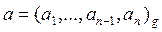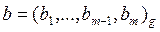
Перенос в другой разряд обозначаем через f (флаг переноса). Находим произведение чисел 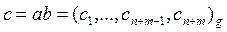. Произведение чисел можно выполнять по формулам:

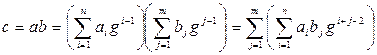,                    (1)

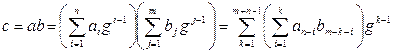 ,                   (2)

где при l <1 мы полагаем a_l = 0, b_l = 0.

Алгоритм, реализуемый по формуле (1) напоминает «умножение столбиком», а по формуле (2) «умножение быстрым столбиком»

Алгоритм умножения неотрицательных целых чисел столбиком.

Вход: , ;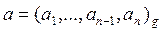

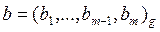c = 0; f:=0;

for j = 1… m;

if b_i > 0 then

for i = 1… n; (f, c_{i + j- 1}): = div (c_{i + j- 1} + a_i b_j + f, g); end for

end if;

End for

Выход: .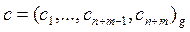

При умножении n -значного числа на m -значное число по этому алгоритму требуется выполнить не более nm операций умножения, nm операций деления с остатком, 2 nm операций сложения.

Алгоритм умножения неотрицательных целых чисел быстрый столбик.

Вход: , ;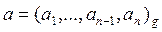

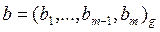c = 0; f:=0;

for k = 1… n+m- 1;       

for i = 1… k;

   if n-i >0 and m-k + i > 0 then f:= f+ a_n-_i · b_m-k+i end if;

end for

(f, c_k): = div (f, g);

End for

Выход: .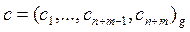

При умножении n -значного числа на m -значное число требуется выполнить nm операций умножения, n + m операций сложения и n + m операций деления с остатком.

В 1962 году студент МГУ, ныне профессор А.А.Карацуба предложил более быстрый способ умножения больших многозначных чисел. Предположим, что у нас имеется два 2 n -значных числа:

, .

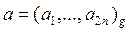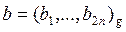Положим

,

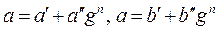где

, .

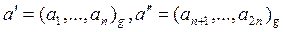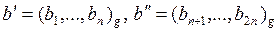Тогда

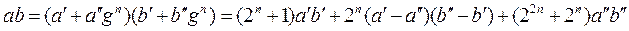. (3)

Таким образом, при умножении двух 2 n -значных чисел по формуле (3) нужно 3 умножения n -значных чисел, 4 сложения и 2 вычитания и 4 сдвига n-значных чисел. По формуле требуется 4 сложения и 3 сдвига. (4) требуется 4 умножения и 3 сдвига.

При больших n метод Карацубы становится более эффективным, чем «быстрый столбец».Если обозначить через T (n) число битовых операций для умножения двух n -разрядных чисел, то

T (2 n) = 3 T (n) + cn,                                      (4)

где c – константа. Используя эти соображения получим, что

.

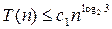Установлено, что существует метод умножения двух n -значных двоичных чисел, требующий не более O(n ·ln n · lnln n) двоичных операций.

Пусть дано целое число

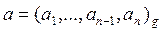
иодноразрядное число b, 1£ b < g. Находим частное 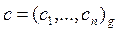 и остаток r.

Алгоритм деления неотрицательного целого числа на однозначное число.

Вход: , ;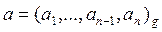

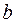r = 0;  

for i = 1… n;       

(c_i, r): = div (rg+a_i, b);

End for

Выход: .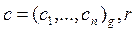

Рассмотрим алгоритм деления целых чисел в общем случае. Задача деления целых чисел упирается в задачу подбора очередной цифры неполного частного в следующей ситуации. Пусть 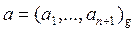, , 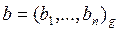причем b_n >0, a / b < g. Нам нужно найти частное от деления a на b:

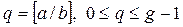.                                           (5)

Условие a / b < g равносильно неравенству a / g < b, что равносильно неравенству

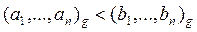                                         (6)

Обозначим

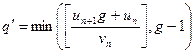                                           (7)

Лемма 1. При указанных выше условиях справедливо неравенство

q £ q `.                                                       (8)

При дополнительном условии b_n > [ g /2] справедливо неравенство

q `-2 £ q.                                                      (9)

Замечание. Чтобы оказаться в рамках второго условия леммы 1 необходимо нормализовать числа a и b, умножив их оба на 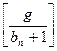. При этом доказывается, что частное q не изменяется.

Алгоритм деления  неотрицательных целых чисел.

Вход: делимое 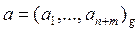, делитель 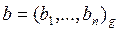, n ³ 2;

Нормализация чисел a и b (нахождение нормализирующего множителя и умножение на него чисел a и b).

(d, k): = div (g, b_n +1);

t:=0; for i = 1… n + m; (t, a_i): = div (tg + da_i, g); end for;

if t >0 then m:= m+ 1; a_m:= t; end if;

t:=0; for i = 1… n; (t, b_i): = div (tg + db_i, g); end for;

for j = m …1; 

Подбор очередной цифры q_m неполного частного. Обеспечение условий подбора очередной цифры (a / b < g, a < gb, e = gb)

e:= (0, b ₁,…, b_n);

p:=1;

for v = 0 … g -1;

      for i =  n …1;

           if b_i > a_n+i   then   p:=1; break else if b_i < a_n+i   then break;  end if;

       end for

         if p =1  then break;end if;

end for

Нахождение приближенного значения q ` цифры q_m неполного частного по формуле (7).

if b_n = a_n+j   then q`:= g - 1 else (q`, t): = div (a_n+j g + a_{n+j- 1}, b_n);  end if;

Уточнение приближенного значения q ` цифры q_m неполного частного.

 while   b_{n- 1} q` > ( a<sub>n+j</sub> g + a<sub>n+j- 1</sub> - b<sub>n</sub>q` ) g + a_{n+j- 2} do  q`:= q`- 1; end while;

Проверка правильности подбора приближенного значения q ` цифры q_m  и ее уточнение:

t:=0; for i = 1… n; (t, a_j+i): = div (a_j+i - q`b_i + tg, g); end for;

q_m := q`;

if t <0 then q_m := q_m -1; t:=0;  

    for i = 1… n; (t, a_j+i): = div (b_i-a_j+i + tg, g); end for;

end if;

q_m := q_m + vg; (не всегда цифра в g -ичной системе счисления.

end for;

Нахождение правильного представления неполного частного и остатка.

 t:=0; for i = 1… n; (t, q_i): = div (q_j + tg, g); end for;

if t >0 then n:= n+ 1; q_m:= t; end if;

t = 0; for i = 1… n; (r_i, t): = div (tg+a_i, d); end for

Выход: неполное частное 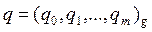, остаток .

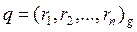Возведение в натуральную степень. Предполагается, что операция умножения многозначных чисел уже реализована. Требуется число a возвести в степень числа m. Представим число m в двоичной системе счисления:

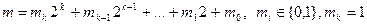.                         (6)

Тогда возможны два возможных алгоритма вычисления степени a^m _, которые получаются из следующих равенств:

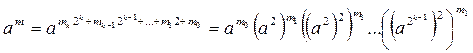,         (7)

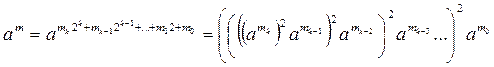.         (8)

Алгоритмы называются бинарными алгоритмами возведения в степень.

В первом случае находятся степени 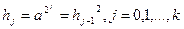. Затем находится произведение всех h_j,, для которых m_i ¹0:

.

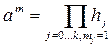Во втором случае находят 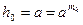, далее

.

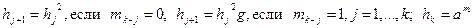Первый алгоритм возведения в степень.

Вход: основание a, показатель степени m;

b:=1; h:= a;

while m  > 0 do  (m, r): = div (m, 2);

if r >0 then b:= bh; end if;

if m > 0 then h:= h·h; end if;

end while;

Выход: b.

Второй  алгоритм возведения в степень.

Вход: основание a, показатель степени m;

b:= a; h:=2 j:=-1;

while m  > 0 do  j:= j +1; (m, m_j): = div (m, 2); end while;

for i = j-1…0; if m_j >0 then b:= b·b·a else b:= b·b; end if; end for;

Выход: b.

Первый способ более экономен в отношении памяти, во втором способе происходит экономия на умножении.