Определение 1. Последовательностью элементов поля Fp называем любое отображение множества неотрицательных целых чисел N 0 в поле Fp:
a: N 0 ® Fp. (1)
Последовательность (1) обозначаем 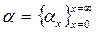 или
или 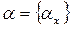 . Множество всех последовательностей вида (1) обозначается через s, последовательность, все члены которой равны нулю обозначаем через 0.
. Множество всех последовательностей вида (1) обозначается через s, последовательность, все члены которой равны нулю обозначаем через 0.
Определение 2. Суммой последовательностей 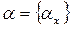 ,
, 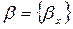 называется последовательность
называется последовательность 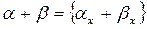 .
.
Определение 3. Произведением последовательности 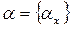 на элемент c Î Fp называется последовательность
на элемент c Î Fp называется последовательность 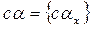 .
.
Определение 4. Сдвигом последовательности 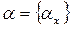 называется последовательность
называется последовательность 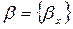 , обозначаемая T ·a, такая, что для любого x Î N 0
, обозначаемая T ·a, такая, что для любого x Î N 0  .
.
Для любого целого неотрицательного числа k Î N 0 символом Tk обозначается k -я степень оператора T, т.о. Tk ·a определяется условием:
Tk ·{a x } ={a x + k }.
Определение 5. Пусть g (l) = b 0l n + b 1l n -1 + …+ bn - 1l + bn Î Fp [l] – многочлен с коэффициентами из поля Fp. Полиномиальным оператором называется такой оператор, обозначаемый символом g, который определен на последовательностях aÎ s, по правилу:
g ·a = b = {b x }Î s,
где для любого x Î N 0
b x = b 0a x + n + b 1a x + n -1 + …+ bn- 1a x + 1 + bn a x,
таким образом,
g ·{a x } = b 0a x + n + b 1a x + n -1 + …+ bn - 1a x + 1 + bn a x.
Последнее равенство через оператор сдвига можно записать следующим образом:
g ·a = b 0 Tn ·a + b 1 Tn- 1·a + …+ bn- 1 T ·a + bn a x.
Через W(s) обозначим множество всех полиномиальных операторов.
Примеры. Пусть
a = {1,2,1,0,0,1,1,2,2,1,1,1,0,0,0,1,…}, b = {0,1,1,1,2,2,0,1,2,1,0,1,0,1,2,1,…}
две последовательности над полем F 3, g (l) = l3 + l2 + 2l +1Î F 3[l]. Тогда
a + b = {1,0,2,1,2,0,1,0,1,2,1,2,0,1,2,2,…},
2a = {2,1,2,0,0,2,2,1,1,2,2,2,0,0,0,2,…},
T ·a = {2,1,0,0,1,1,2,2,1,1,1,0,0,0,1,…},
T 2 ·a = {1,0,0,1,1,2,2,1,1,1,0,0,0,1,…},
T 3 ·a = {0,0,1,1,2,2,1,1,1,0,0,0,1,…},
g ·a = {0,1,0,2,2,1,2,0,0,1,0,1,1,…},
Теорема 1. Система (s, +) – абелева аддитивная группа.
Доказательство. По определению 2 операция сложения последовательностей из s бинарная алгебраическая, и для нее выполняются ассоциативный и коммутативный законы. Нулевым элементом является последовательность 0 = {0}, противоположным элементом для последовательности 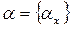 является последовательность
является последовательность 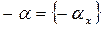 .
.
Теорема 2. Система (s, +, Fp) – векторное пространство над полем Fp, замкнутое относительно сдвига.
Доказательство. По теореме 1 система (s, +) – аддитивная абелева группа. Согласно определению 3 на множестве s определена операция умножения элементов множества s на элементы поля Fp. Так как для любой последовательности aÎ s, последовательность T ·a Î s,и так как любая последовательности 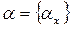 Î s может быть получена сдвигом последовательности b = {b x }Î s, где для любого a = {a x }, T ·a = b = {b x }, имеем b x + 1 = a x, а b0 – произвольный элемент из Fp. Поэтому T · s = s.
Î s может быть получена сдвигом последовательности b = {b x }Î s, где для любого a = {a x }, T ·a = b = {b x }, имеем b x + 1 = a x, а b0 – произвольный элемент из Fp. Поэтому T · s = s.
Теорема 3. Многочлены g (l) и h (l) равны тогда и только тогда, когда равны соответствующие им полиномиальные операторы g и h, т.е.
g (l) = h (l) Û ("aÎ s)[ g ·a = h ·a].
Доказательство. Пусть
g (l) = b 0 + b 1l k + …+ bk- 1l k -1 + bk l k, h (l) = c 0 + c 1l + …+ cm- 1l m -1 + cm l m Î Fp [l].
Пусть g (l) = h (l). Тогда k = m и bi = ci для любого i = 0, 1,…, k. Поэтому для любой последовательности aÎ s имеем
g ·a = b 0 a + b 1 T ·a + …+ bk Tk ·a = c 0a + c 1 T ·a + …+ cm Tm ·a = h ·a.
Пусть ("aÎ s)[ g ·a = h ·a]. Докажем, что g (l) = h (l). Для определенности пусть k £ m. Далее пусть g ·d = a = {a x }, g ·d = b = {b x }. Для каждого неотрицательного числа j выберем последовательность d с условиями: d x = 0, x ¹ j и d j = 1.
Если j £ k, то получаем
g ·d = b 0 d + b 1 T ·d + …+ bkTk · d ,
g ·d0 = b 0 d0 + b 1 T ·d0 + …+ bk Tk ·d0 = b 0 d0 + b 1d1 + …+ bk d k = b j,
h ·d = c 0d + c 1 T ·d + …+ bmTm · d ,
h ·d0 = c 0d0 + c 1 T 1·d0 + …+ cm Tm ·d0 = c 0d0 + c 1d1 + …+ cm d m = cj.
Отсюда получаем bj = cj для j = 0, 1,…, k.
Если k < j £ m, то получаем
g ·d = b 0 d + b 1 T ·d + …+ bkTk · d,
g ·d0 = b 0 d0 + b 1 T ·d0 + …+ bk Tk ·d0 = b 0 d0 + b 1d1 + …+ bk d k = 0,
h ·d = c 0d + c 1 T ·d + …+ bmTm · d,
h ·d0 = c 0d0 + c 1 T 1·d0 + …+ cm Tm ·d0 = c 0d0 + c 1d1 + …+ cm d m = cj.
Отсюда получаем cj = 0 для j = k – 1,…, m. Таким образом, соответствующие коэффициенты многочленов g (l) и h (l) равны и поэтому g (l) = h (l).
Теорема 4. Для любых многочленов g (l) и h (l)Î Fp [l] и для любых последовательностей a, bÎ s справедливы равенства:
1) g ·(a + b) = g ·a + g ·b;
2) (g + h)·a = g ·a + h ·a;
3) g ·(h ·a) = (gh)·a.
Доказательство. 1. Пусть a = {a x }, b = {b x }, g (l) = b 0 + b 1l + …+ bk - 1l k -1 + bk l k Î Fp [l]. Так как для любого x Î N 0
g ·(a x + b x) = b 0 (a x + b x) + b 1 T ·(a x + b x) + …+ bk Tk ·(a x + b x) =
= b 0 (a x + b x) + b 1(a x +1 + b x +1) + …+ bk (a x+k + b x+k) =
= (b 0 a x + b 1a x +1 + …+ bk a x+k) + (b 0 b x + b 1b x +1 + …+ bk b x+k) =
= (b 0 a x + b 1 T ·a x + …+ bk Tk ·a x) + (b 0b x + b 1 T ·b x + …+ bk Tk b x) = g ·a x + g ·b x,
то g ·(a + b) = g ·a + g ·b.
2. Пусть a = {a x }, g (l) = b 0 + b 1l + …+ bk l k, h (l) = c 0 + c 1l + …+ cm l m Î Fp [l], k £ m. Для каждого i, k < i £ m, положим bi = 0. Тогда g (l)+ h (l) = (b 0 + c 0)+ (b 1+ c 1)l + …+ (bm + cm)l m. Так как для любого x Î N 0
(g + h)·a x = (b 0+ c 0 )a x + (b 1+ c 1) T ·a x + …+(bm + cm) Tm ·a x =
= (b 0+ c 0 )a x + (b 1+ c 1)a x +1 + …+(bm + cm)a x+m =
= (b 0 a x + b 1a x +1 + …+ bm a x+m) + (c 0 a x + c 1a x +1 + …+ cm a x+m) =
= (b 0 a x + b 1 T ·a x + …+ bm Tm ·a x) + (c 0 a x + c 1 T ·a x + …+ cm Tm ·a x) = g ·a x + h ·a x,
то (g + h)·a = g ·a + h ·a.
3. Пусть a = {a x }, g (l) = b 0 + b 1l + …+ bk l k, h (l) = c 0 + c 1l + …+ cm l m Î Fp [l].
Тогда для любого x Î N 0
h ·a x = c 0a x + c 1 T ·a x + …+ cmTm ·a x =
Поэтому
g ·(h ·a) = b 0(c 0 a x + c 1a x +1 + …+ cm a x+m) + b 1(c 0 a x +1 + c 1a x +2 + …+ cm a x + m +1) +…+
. + bk (c 0 a x + k + c 1a x +1+ k + …+ cm a x+m + k ) = 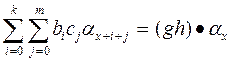 .
.
Отсюда получаем, что g ·(h ·a) = (gh)·a.
Теорема 5. Система полиномиальных операторов (W(s), +, ×) образует кольцо, изоморфное кольцу многочленов Fp [l].
Доказательство. С многочленом g (l) = b 0 + b 1l + …+ bk l k Î Fp [l] сопоставим полиномиальный оператор линейный
g = b 0 + b 1 T + …+ bk Tk Î W(s).
В силу теоремы 3 это соответствие взаимно однозначное. Операции сложения и умножения для операторов g, h Î W(s) определяем соотношениями:
g + h = u Û ("dÎ s)[ u ·d= g ·d + h ·d],
g · h = v Û ("dÎ s)[ v ·d= g ·(h ·d)].
Тогда по теореме 5 получаем, отображение g (l)® g сумме и произведению многочленов из Fp [l] ставит в соответствие сумму и произведение операторов из W(s). Следовательно, указанное отображение является изоморфизмом.



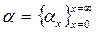 или
или 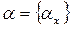 . Множество всех последовательностей вида (1) обозначается через s, последовательность, все члены которой равны нулю обозначаем через 0.
. Множество всех последовательностей вида (1) обозначается через s, последовательность, все члены которой равны нулю обозначаем через 0.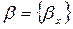 называется последовательность
называется последовательность 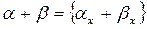 .
.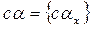 .
. .
.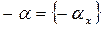 .
.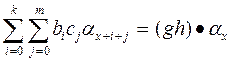 .
.

