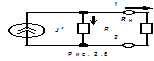Рис1 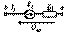

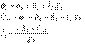 Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.
Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.
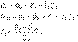
Объединяя оба случая, получим  1
1
или для постоянного тока 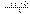 2
2
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.
Электрический баланс в электрических цепях (баланс мощностей).
При протекании токов по резистивным элементам в этих элементах выделяется теплота (энергия). По закону сохранения энергии количество энергии выделяемой в цепи должно равняться количеству энергии которую поставляют в цепи источники ЭДС и тока в единицу времени. Согласно закону Д. Ленца количество выделяемой энергии на резисторе равняется: 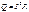 .
.
Количество энергии выделяемой источником ЭДС: 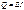
Количество энергии которое выделяет и.т. 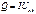 , где
, где 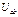 - напряжение на зажимах источника:
- напряжение на зажимах источника: 
В соответствии с законом сохранения энергии уравнение баланса мощностей в цепи:
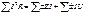
«+» ставиться если ЭДС и ток сонаправлены, I и U противоположно направлены
Первый закон Кирхгофа.
Закон устанавливает, что вследствие непрерывности тока суммарный ток, втекающий в какой-либо замкнутый объем, равен суммарному вытекающему из этого объема току. В теории цепей под замкнутым объемом понимается узел или отсечение. Чаще всего первый закон Кирхгофа формулируют для любого узла: 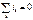
Для узла, изображенного на рис. 2.23, узловое уравнение будет таким: 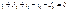
Иногда уравнение записывают, выделяя источники тока:
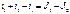 , то есть
, то есть 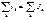
Важно только соблюдать правило знаков: все истинные направления входящих токов считаются положительными, а выходящие — отрицательными
Второй закон Кирхгофа
Напомним, что напряжение на двухполюсных элементах — это разность потенциалов на его зажимах:
Нетрудно убедиться в том, что для схемы, изображенной на рис. 2.26,

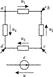 то есть сумма напряжений на двухполюсниках любого замкнутого контура равна нулю.
то есть сумма напряжений на двухполюсниках любого замкнутого контура равна нулю.
Конечно, это будет справедливо, если соблюдать правило знаков: 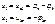
и т. д.
Если какие-либо из двухполюсников представляют собой источники ЭДС, то с учетом взаимного направления е и u можно записать контурное уравнение: 
В левой его части используются напряжения со знаком «+», совпадающие с направлением обхода контура, в правой — ЭДС, совпадающие с тем же направлением обхода. Для представления уравнений второго закона Кирхгофа относительно тех же переменных (токов) используются приведенные ранее компонентные уравнения.
Метод узловых потенциалов.
Метод узловых потенциалов является одним из основных расчетных методов. Суть метода заключается в том, что при использовании законов Кирхгофа и Ома определяются потенциалы узлов схемы, а затем и токи ветвей. Число решаемых уравнений сокращается до величины ( у – 1). Если в схеме «у» узлов, то потенциал одного (базового) узла можно выбрать произвольно, приравняв его значение, например, нулю. Уравнения для нахождения потенциалов других узлов составляются по определенным правилам. Лучше всего это показать на примере. Рассмотрим схему рис. 1.21. Число узлов у = 4; примем потенциал 0-го узла равным нулю (φ0 = 0).Для остальных узлов запишем уравнения по первому затону Кирхгофа. Для 1-го узла: 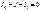 Для 2-го узла:
Для 2-го узла: 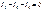
Для 3-го узла: 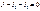 Используя закон Ома, выразим токи через потенциалы узлов и параметры ветвей.
Используя закон Ома, выразим токи через потенциалы узлов и параметры ветвей.



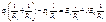
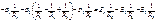
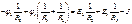
Используем выражение 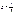 . Кроме этого, введем дополнительные обозначения
. Кроме этого, введем дополнительные обозначения
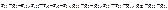 где
где 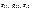 – сумма проводимостей ветвей, присоединённых соответственно к 1, 2 и 3 узлам, т. е. к узлам, потенциалы которых подлежат определению; g12 = g21 – сумма проводимостей
– сумма проводимостей ветвей, присоединённых соответственно к 1, 2 и 3 узлам, т. е. к узлам, потенциалы которых подлежат определению; g12 = g21 – сумма проводимостей
ветвей, соединяющих два соседних узла 1 и 2; g23 = g32 – сумма проводимостей ветвей, соединяющих два соседних узла 2 и 3. В правой части уравнений находится алгебраическая сумма произведений ЭДС на проводимости соответствующих ветвей и токов источников тока. Причем, произведение или ток источника берутся со знаком «+», если ЭДС или источник тока действуют к узлу, и со знаком «–» – если наоборот. Следуя по пути дальнейшей формализации, можно обозначить правые части уравнений как узловые токи: 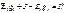 ;
; 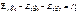 ;
; 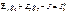 Окончательно система узловых уравнений выглядит так:
Окончательно система узловых уравнений выглядит так:
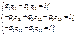
Для определения потенциалов исследуемой цепи нужно решить только три уравнения (вместо пяти – по законам Кирхгофа), т. е. число уравнений системы значительно сократилось.После определения потенциалов узлов но закону Ома определяются токи во всех ветвях схемы
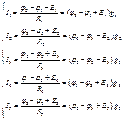
Рекомендуется следующий порядок расчета электрической цепи по методу узловых потенциалов.
1. Определить число у узлов схемы; пронумеровать узлы.2. Один из узлов схемы принять за базовый, положив его потенциал равным нулю.3. Подсчитать проводимости ветвей, если даны их сопротивления.4. Подсчитать сумму проводимостей всех ветвей, присоединенных к каждому узлу, потенциал которого подлежит определению (это проводимости с одинаковыми индексами, например, g11, g22 и т. д.).5. Определить сумму проводимостей ветвей между каждой парой соседних узлов, потенциалы которых подлежат определению (это проводимости с разными индексами, например g12, g23 и т.д.).6. Для записи правой части уравнений системы (1.17) необходимо определить узловые токи 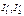 и т. д.7. Записать систему уравнении (1.17), причем, например, для первого узла: потенциал
и т. д.7. Записать систему уравнении (1.17), причем, например, для первого узла: потенциал 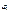 берется со знаком «+» (плюс), остальные со знаком «–» (минус) и т. д. 8. Решить систему (1.17).9. По (1.18) определять токи
берется со знаком «+» (плюс), остальные со знаком «–» (минус) и т. д. 8. Решить систему (1.17).9. По (1.18) определять токи
Метод контурных токов.
Другим важным методом является метод контурных токов, в основе которого также лежат уравнения Кирхгофа.В расчет вводятся контурные токи, замыкающиеся по независимым контурам. Для них составляются уравнения по второму закону Кирхгофа. Действительные токи в ветвях схемы определяются как алгебраическая сумма контурных токов. При этом первый закон Кирхгофа удовлетворяется автоматически. Число решаемых уравнений сокращается до числа независимых контуров «k» (см. п. 1.5). Лучше всего переход от уравнений, составленных по законам Кирхгофа, к контурным уравнениям можно показать на примере. Рассмотрим снова схему рис. 1.21. Перерисуем её ещё раз (см. рис. 1.24). Это нужно для того, чтобы не затемнять чертеж. Для схемы рис. 1.24 составляем уравнения по законам Кирхгофа. По первому затону – для узлов 1, 2, 3; по второму закону – для 1-го и 2-го независимых контуров (см. рис. 1.24).Направление обхода контуров указано там же 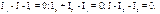
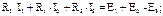
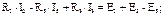 Выразим из первых трех уравнении токи I3, I4, I5 через I1, I2 и J:
Выразим из первых трех уравнении токи I3, I4, I5 через I1, I2 и J:  Полученные значения I3, I4, I5 подставим в два последних уравнения, которые составлены для независимых контуров. После несложных преобразований имеем
Полученные значения I3, I4, I5 подставим в два последних уравнения, которые составлены для независимых контуров. После несложных преобразований имеем 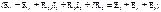
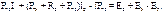 Из последних уравнений видно, что ток I1 замыкается только по первому независимому контуру; ток I2 – только по второму независимому контуру; по сопротивлению R3 (общему для обоих независимых контуров) протекает как ток I1, так и ток I2; ток источника тока J замыкается по 4-ой и 5-й ветвям схемы (см. рис. 1.24), и слагаемые JR4 и - JR5 представляют собой падения напряжения на сопротивлениях R4 и R5 от тока J источника тока. Введем обозначения:
Из последних уравнений видно, что ток I1 замыкается только по первому независимому контуру; ток I2 – только по второму независимому контуру; по сопротивлению R3 (общему для обоих независимых контуров) протекает как ток I1, так и ток I2; ток источника тока J замыкается по 4-ой и 5-й ветвям схемы (см. рис. 1.24), и слагаемые JR4 и - JR5 представляют собой падения напряжения на сопротивлениях R4 и R5 от тока J источника тока. Введем обозначения: 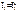 = – первый контурный ток;
= – первый контурный ток; 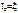 = – второй контурный ток. Члены JR4 и - JR5 можно записать в правой части уравнений. Тогда уравнения для контурных токов можно записать в более компактном виде
= – второй контурный ток. Члены JR4 и - JR5 можно записать в правой части уравнений. Тогда уравнения для контурных токов можно записать в более компактном виде 
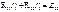 (1,19)где
(1,19)где  – собственное сопротивление 1-гo контура;
– собственное сопротивление 1-гo контура; 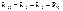 – собственное сопротивление 2-го контура;
– собственное сопротивление 2-го контура;  – общее сопротивление 1-го и 2-го контуров;
– общее сопротивление 1-го и 2-го контуров;  – контурная ЭДС 1-го контура;
– контурная ЭДС 1-го контура;  – контурная ЭДС 2-го контура. Общее решение системы уравнений (1.19) относительно контурных токов будет таково:
– контурная ЭДС 2-го контура. Общее решение системы уравнений (1.19) относительно контурных токов будет таково:

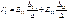 , где
, где 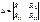 – определитель системы. Алгебраическое дополнение Δmn получено из определителя путем вычеркивания «m»-ой строки и «n»-го столбца и умножения полученного определителя на (–1)m+n. Определитель системы Δ обладает симметрией относительно гласной диагонали (R12 = R21 =R5) и в силу этого Δmn = Δnm. В рассматриваемом примере число независимых контуров равно двум, однако это не умаляет общности всех рассуждений, т. е. все выкладки могут быть распространены на любое число независимых контуров. По методу контурных токов составляются уравнения только по второму закону Кирхгофа. Это приводит к уменьшению числа решаемых уравнений. Порядок расчета цепи по методу контурных токов. 1. Определить независимые контуры рассматриваемой цепи. Пронумеровать их. 2. Выбрать произвольно направление обхода независимых контуров. Направление контурного тока и направление обхода контура совпадают. 3. Если в схеме есть источник тока, то надо, считая ток источника за контурный ток, наметить произвольный путь, по которому он будет замыкаться. 4. Составить уравнения по второму закону Кирхгофа для всех независимых контуров. При этом надо учесть падение напряжения от тока источника тока. 5. Определить контурные токи. 6. Определить действительные токи в ветвях.
– определитель системы. Алгебраическое дополнение Δmn получено из определителя путем вычеркивания «m»-ой строки и «n»-го столбца и умножения полученного определителя на (–1)m+n. Определитель системы Δ обладает симметрией относительно гласной диагонали (R12 = R21 =R5) и в силу этого Δmn = Δnm. В рассматриваемом примере число независимых контуров равно двум, однако это не умаляет общности всех рассуждений, т. е. все выкладки могут быть распространены на любое число независимых контуров. По методу контурных токов составляются уравнения только по второму закону Кирхгофа. Это приводит к уменьшению числа решаемых уравнений. Порядок расчета цепи по методу контурных токов. 1. Определить независимые контуры рассматриваемой цепи. Пронумеровать их. 2. Выбрать произвольно направление обхода независимых контуров. Направление контурного тока и направление обхода контура совпадают. 3. Если в схеме есть источник тока, то надо, считая ток источника за контурный ток, наметить произвольный путь, по которому он будет замыкаться. 4. Составить уравнения по второму закону Кирхгофа для всех независимых контуров. При этом надо учесть падение напряжения от тока источника тока. 5. Определить контурные токи. 6. Определить действительные токи в ветвях.
7. Уравнение цепи в матричной форме
Сначала введем понятие обобщенной ветви (рис. 3.3).
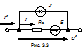
Для нее можно записать по первому закону Кирхгофа
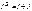 (3.6)
(3.6)
И по обобщенному закону Ома
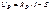 (3.7)
(3.7)
Напряжение на резисторе ветви R В по закону Ома
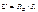 (3.8)
(3.8)
Или для тока через проводимость ветви 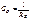
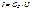 (3.9)
(3.9)
Закон Ома в матричной форме
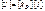 (3.10)
(3.10)
или
 (3.11)
(3.11)
где [ U ] и [ I ] – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы, а
 и
и  причем k равно числу ветвей схемы.
причем k равно числу ветвей схемы.
Например, для схемы рис. 3.1
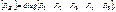 а
а 
Обобщенный закон Ома в матричной форме, исходя из (3.7), получим в виде
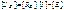
где [ U в] и [ I в] – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы.
Для схемы рис. 3.1
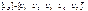

Вводится понятие узловой матрицы [ А ].
Узловая матрица – это прямоугольная матрица, строки которой соответствуют узлам, а столбцы – ветвям направленного графа схемы.
Число строк матрицы равно числу независимых узлов. Элементы матрицы а ij, где (i – номер строки, j – номер столбца, принимают значения 1, – 1 или 0.
Элементы а ij = 1, если ветвь j соединена с узлом i и направлена от него.
Элементы а ij = - 1, если ветвь j соединена с узлом i и направлена k этому узлу. Элементы а ij = 0, если ветвь j не соединена с узлом i.
Например, в схеме рис. 3.1 и 3.2

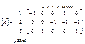 (3.13)
(3.13)
С помощью матрицы [ А ] запишем первый закон Кирхгофа с учетом (3.6)
 (3.14)
(3.14)
или
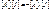 (3.15)
(3.15)
где [ J ] – столбцовая матрица источников тока, число строк которой совпадает с числом ветвей схемы.
Для схемы рис. 3.1 [ J ] = [0 0 0 – J J ] T, т. е. ток источника тока J замыкается по четвертой и пятой ветвям.
Матрица контуров [ В ] – прямоугольная матрица, строки которой соответствуют контурам, а столбцы – ветвям направленного графа схемы. Число строк равно числу независимых контуров. Элементы матрицы в ij, где i – номер строки, j – номер столбца, принимают значения 1, –1 или 0. Элементы в ij = 1, если ветвь j содержится в контуре i и направление ветви совпадает с направлением обхода контура. Элементы в ij = – 1, если ветвь j содержится в контуре i и направление ветви противоположно направлению обхода контура. Элементы в ij = 0, если ветвь j не содержится в контуре i.
Например, в схеме рис. 3.1 и 3.2
 (3.16)
(3.16)
С помощью матрицы В запишем второй закон Кирхгофа с учетом (3.12)
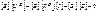 (3.17)
(3.17)
или
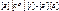
8. Матричная форма записи метода контурных токов
Уравнения метода контурных токов выводятся из уравнений, составленных,по второму закону Кирхгофа. Подставим в матричное уравнение (3.18) уравнение (3.14), соответствующее первому закону Кирхгофа, переписав его предварительно таким образом
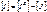 (3.19)
(3.19)
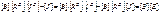 (3.20)
(3.20)
 или
или
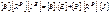 (3.21)
(3.21)
Можно показать, что с помощью транспонированной контурной матрицы [ В ] Т токи ветвей схемы [/в] могут быть выражены через матрицу контурных токов [/к]
 (3.22)
(3.22)
где [/к]–столбцовая матрица контурных токов. Тогда выражение (3.21) примет вид
 (3.23)
(3.23)
или в более компактной форме
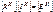 (3.24)
(3.24)
где
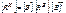 – матрица контурных сопротивлений;
– матрица контурных сопротивлений; 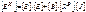 – матрица контурных ЭДС.
– матрица контурных ЭДС.
Матрицы уравнения (3.23) более просты для составления, поэтому уравнением (3.23) пользуются при решении на ЭВМ.
После решения уравнения (3.23) относительно контурных токов схемы решают последовательно уравнение (3.22) относительно токов ветвей и (3.19) относительно токов в резисторах.
9. Узловые Уравнения в матричной форме.
Уравнение для узловых потенциалов выводят из уравнений, составленных по первому закону Кирхгофа для исследуемой схемы.
Подставив в матричное уравнение (3.15) матрицу [ I ] из (3.11). получим
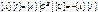 (3.25)
(3.25)
Уравнение (3.12) с учётом (3.10) может быть записано в такой форме
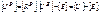 (3.26)
(3.26)
Можно показать, что с помощью транспонированной узловой матрицы [ А ]Т, матрица напряжений ветвей схемы [ U B] может быть выражена через матрицу потенциалов узлов [ j ] в таком виде
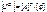 -(3.26) (3.27)
-(3.26) (3.27)
где [ j ] - столбовая матрица потенциалов узлов схемы.
Уравнение (3.26). переписанное относительно матрицы [ U ] и с учётом (3.27). запишем так
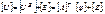 -(3.27). (3.28)
-(3.27). (3.28)
Теперь уравнение (3.25) с учётом (3.28) примет вид
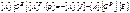 -(3.28) (3.29)
-(3.28) (3.29)
Произведение матриц [ А ][ G В][ А ]Т даёт матрицу узловых проводимостей [ G У], а правая часть уравнения (3.29) представляет собой матрицу узловых токов [ J У]. Теперь уравнение (3.29) примет вид
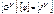 (3.30)
(3.30)
При составлении матрицы [ G У] следует учесть, что g ii > 0, g ik < 0 (см. уравнение 1.17).
Уравнения (3.28) и (3.29) являются узловыми уравнениями в матричной форме.
Матрицы уравнения (3.29) наиболее простые для составления, поэтому для ввода матриц в ЭВМ пользуются именно этим уравнением.
После решения уравнения (3.29) на ЭВМ относительно потенциалов [ j ], решается уравнение (3.27) относительно [ U B], далее (3.28) относительно [ U ] и (3.11) относительно [ I ].
Перечисленные матрицы выводятся в качестве выходных данных.
10.Преобразование пассивного треугольника сопротивлений в звезду и обратно
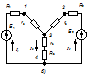
Рассмотрим преобразование схем, в которых резисторы соединены в эквивалентные треугольник (рис. 2.5 а) и звезду (рис. 2.5 б).
Как отмечалось выше, условие эквивалентности двух схем сводится к равенству токов протекающих к узлам 1, 2, 3 треугольника и к соответствующим точкам звезды – это токи I 1, I 2, I 3, а также к равенству напряжений между этими же точками.
Запишем напряжение U 21 для треугольника и звезды при условии I 2 = 0; I 3 = - I 1.
В треугольнике по сопротивлению R 12 протекает ток  , являющийся частью тока I 3 (так как I 2 = 0), который мы найдем по формуле «разброса токов»
, являющийся частью тока I 3 (так как I 2 = 0), который мы найдем по формуле «разброса токов»
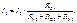 (2.3)
(2.3)
Отсюда напряжение
 (2.4)
(2.4)
Это же напряжение для эквивалентной звезды (с учетом I 2 = 0)
 ;
;  ;
; 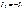 ;
;  . (2.5)
. (2.5)
Приравнивая (2.4) и (2.5), получим
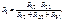 (2.6)
(2.6)
Аналогично (2.6) можно записать
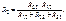
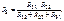 (2.7)
(2.7)
(2.8)
Формулы (2.6), (2.7) и (2.8) позволяют по известным сопротивлениям исходного треугольника получить сопротивления лучей эквивалентной звезды.
При обратном преобразовании, если за исходную схему берем трёхлучевую звезду, то сопротивления эквивалентного треугольника получим, решая совместно уравнения (2.6), (2.7) и (2.8) относительно неизвестных параметров треугольника
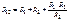 ;
; 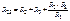 (2.9); (2.10)
(2.9); (2.10)
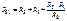 ; (2.11)
; (2.11)
Обратите внимание на

известную мнемонику формул (2.6) – (2.11), позволяющую довольно просто их запомнить. Например, сопротивление R 1 по (2.6) для эквивалентной звезды получаем как произведение сопротивлений R 12 и R 31, подключенных к 1 узлу треугольника, деленное на сумму всех его сопротивлений.
Сопротивление, например, R 12 по (2.9) получается как сумма сопротивлений R 1 и R 2 (обратите внимание на их индексы) и сопротивления R 1 × R 2 / R 3 (внимание на индексы).
11. Преобразование параллельного соединения ветвей с источниками ЭДС и тока.
Если сложная электрическая схема содержит некоторое количество ветвей с источниками ЭДС или тока, соединенных параллельно, то расчет такой схемы может быть существенно облегчен путем замены параллельных ветвей одной ветвью с эквивалентными сопротивлением и ЭДС или эквивалентным источником тока. Проиллюстрируем сказанное на примере схемы, приведенной на рис. 2.7. На схеме рис. 2.7 а между точками 1 и 2 подключены две ветви с источниками ЭДС E1 и E2 и сопротивлениями R1 и R2. К этим же точкам подключен источник тока J3. Требуется заменить часть схемы слева от точек 1 и 2 на эквивалентную с источником ЭДС Е и внутренним сопротивлением R, как на рис. 2.7 б, либо на схему с источником тока JУ и внутренним сопротивлением R. Условием эквивалентности является одинаковая для всех трех схем мощность, выделяющаяся на RН. Для этого необходимо, чтобы при заданном RН напряжение U и ток I в нём оставались неизменными.
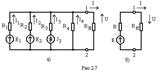
Для схемы рис. 2.7 а по первому закону Кирхгофа запишем I = I 1 + I 2 + I 3 + I 4 (2.12) или, используя обобщенный закон Ома,
I=(E1-U)g1+(-E2-U)g2+J3-Ug4=E1g1-E2g2+J3-U(g1+g2+g4)
(2.13) где
g1=1/R1;
g2=1/R2;
g4=1/R4;
В схеме рис. 2.7 ток I=(E-U)g=Eg-Ug (2.14) В схеме рис. (2.8)
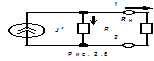
I = JY - Ib = JY - Ug ( 2.15) где JY – эквивалентный источник тока.
Так как условия эквивалентности должны выполняться при любых напряжениях U и токах I, то приравнивая правые части (2.13) и (2.14), а также (2.13) и (2.15), получим E 1 g 1 - E 2 g 2 + J 3 - U (g 1 + g 2 + g 4)= Eg - Ug; E 1 g 1 - E 2 g 2 + J 3 - U (g 1 + g 2 + g 4)= JY - Ug
Из последних уравнений следует g= g 1+ g 2+ g 4=Σ gk (2.16) JY = E 1 g 1 - E 2 g 2 + J 3 (2.17)
E = (E 1 g 1 - E 2 g 2 + J 3) / (g 1+ g 2+ g 4)= JY / Σ gk (2.18)
Обратим внимание на то, что эквивалентная проводимость g является суммой проводимостей всех ветвей независимо от того, есть или нет в данной ветви ЭДС. Исключение составляет источник тока J3 – проводимость этого участка цепи равна нулю и может не учитываться при подсчете проводимости g. Так как сопротивление идеального источника тока равно бесконечности, то сопротивление R3, соединенное последовательно с J3, не меняет величину сопротивления, а значит, и проводимости ветви источника тока. Вместе с тем, значение эквивалентной ЭДС Е, как и эквивалентного источника тока JY, зависят от величин ЭДС Е1 и Е2 и тока J3. Правило знаков получим из (2.17) и (2.18). Если стрелки источников ЭДС и источников тока направлены так же как стрелки эквивалентных Е и JY, т. е. к точке 1 (см. рис. 2.7 а), то берут соответствующие слагаемые со знаком плюс. В нашем случае это Е1 и J3. Для ветви с Е2 знак противоположный.





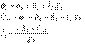 Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.
Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.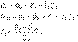
 1
1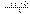 2
2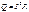 .
.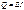
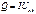 , где
, где 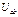 - напряжение на зажимах источника:
- напряжение на зажимах источника: 
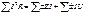
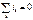
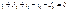
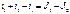 , то есть
, то есть 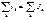

 то есть сумма напряжений на двухполюсниках любого замкнутого контура равна нулю.
то есть сумма напряжений на двухполюсниках любого замкнутого контура равна нулю.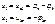

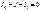 Для 2-го узла:
Для 2-го узла: 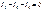
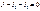 Используя закон Ома, выразим токи через потенциалы узлов и параметры ветвей.
Используя закон Ома, выразим токи через потенциалы узлов и параметры ветвей.


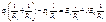
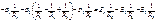
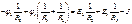
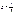 . Кроме этого, введем дополнительные обозначения
. Кроме этого, введем дополнительные обозначения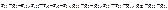 где
где 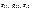 – сумма проводимостей ветвей, присоединённых соответственно к 1, 2 и 3 узлам, т. е. к узлам, потенциалы которых подлежат определению; g12 = g21 – сумма проводимостей
– сумма проводимостей ветвей, присоединённых соответственно к 1, 2 и 3 узлам, т. е. к узлам, потенциалы которых подлежат определению; g12 = g21 – сумма проводимостей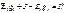 ;
; 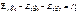 ;
; 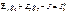 Окончательно система узловых уравнений выглядит так:
Окончательно система узловых уравнений выглядит так: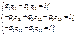
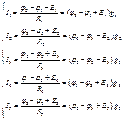
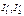 и т. д.7. Записать систему уравнении (1.17), причем, например, для первого узла: потенциал
и т. д.7. Записать систему уравнении (1.17), причем, например, для первого узла: потенциал 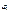 берется со знаком «+» (плюс), остальные со знаком «–» (минус) и т. д. 8. Решить систему (1.17).9. По (1.18) определять токи
берется со знаком «+» (плюс), остальные со знаком «–» (минус) и т. д. 8. Решить систему (1.17).9. По (1.18) определять токи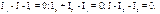
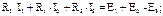
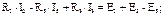 Выразим из первых трех уравнении токи I3, I4, I5 через I1, I2 и J:
Выразим из первых трех уравнении токи I3, I4, I5 через I1, I2 и J:  Полученные значения I3, I4, I5 подставим в два последних уравнения, которые составлены для независимых контуров. После несложных преобразований имеем
Полученные значения I3, I4, I5 подставим в два последних уравнения, которые составлены для независимых контуров. После несложных преобразований имеем 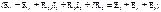
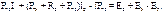 Из последних уравнений видно, что ток I1 замыкается только по первому независимому контуру; ток I2 – только по второму независимому контуру; по сопротивлению R3 (общему для обоих независимых контуров) протекает как ток I1, так и ток I2; ток источника тока J замыкается по 4-ой и 5-й ветвям схемы (см. рис. 1.24), и слагаемые JR4 и - JR5 представляют собой падения напряжения на сопротивлениях R4 и R5 от тока J источника тока. Введем обозначения:
Из последних уравнений видно, что ток I1 замыкается только по первому независимому контуру; ток I2 – только по второму независимому контуру; по сопротивлению R3 (общему для обоих независимых контуров) протекает как ток I1, так и ток I2; ток источника тока J замыкается по 4-ой и 5-й ветвям схемы (см. рис. 1.24), и слагаемые JR4 и - JR5 представляют собой падения напряжения на сопротивлениях R4 и R5 от тока J источника тока. Введем обозначения: 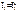 = – первый контурный ток;
= – первый контурный ток; 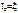 = – второй контурный ток. Члены JR4 и - JR5 можно записать в правой части уравнений. Тогда уравнения для контурных токов можно записать в более компактном виде
= – второй контурный ток. Члены JR4 и - JR5 можно записать в правой части уравнений. Тогда уравнения для контурных токов можно записать в более компактном виде 
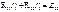 (1,19)где
(1,19)где  – собственное сопротивление 1-гo контура;
– собственное сопротивление 1-гo контура; 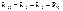 – собственное сопротивление 2-го контура;
– собственное сопротивление 2-го контура;  – общее сопротивление 1-го и 2-го контуров;
– общее сопротивление 1-го и 2-го контуров;  – контурная ЭДС 1-го контура;
– контурная ЭДС 1-го контура;  – контурная ЭДС 2-го контура. Общее решение системы уравнений (1.19) относительно контурных токов будет таково:
– контурная ЭДС 2-го контура. Общее решение системы уравнений (1.19) относительно контурных токов будет таково:
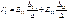 , где
, где 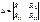 – определитель системы. Алгебраическое дополнение Δmn получено из определителя путем вычеркивания «m»-ой строки и «n»-го столбца и умножения полученного определителя на (–1)m+n. Определитель системы Δ обладает симметрией относительно гласной диагонали (R12 = R21 =R5) и в силу этого Δmn = Δnm. В рассматриваемом примере число независимых контуров равно двум, однако это не умаляет общности всех рассуждений, т. е. все выкладки могут быть распространены на любое число независимых контуров. По методу контурных токов составляются уравнения только по второму закону Кирхгофа. Это приводит к уменьшению числа решаемых уравнений. Порядок расчета цепи по методу контурных токов. 1. Определить независимые контуры рассматриваемой цепи. Пронумеровать их. 2. Выбрать произвольно направление обхода независимых контуров. Направление контурного тока и направление обхода контура совпадают. 3. Если в схеме есть источник тока, то надо, считая ток источника за контурный ток, наметить произвольный путь, по которому он будет замыкаться. 4. Составить уравнения по второму закону Кирхгофа для всех независимых контуров. При этом надо учесть падение напряжения от тока источника тока. 5. Определить контурные токи. 6. Определить действительные токи в ветвях.
– определитель системы. Алгебраическое дополнение Δmn получено из определителя путем вычеркивания «m»-ой строки и «n»-го столбца и умножения полученного определителя на (–1)m+n. Определитель системы Δ обладает симметрией относительно гласной диагонали (R12 = R21 =R5) и в силу этого Δmn = Δnm. В рассматриваемом примере число независимых контуров равно двум, однако это не умаляет общности всех рассуждений, т. е. все выкладки могут быть распространены на любое число независимых контуров. По методу контурных токов составляются уравнения только по второму закону Кирхгофа. Это приводит к уменьшению числа решаемых уравнений. Порядок расчета цепи по методу контурных токов. 1. Определить независимые контуры рассматриваемой цепи. Пронумеровать их. 2. Выбрать произвольно направление обхода независимых контуров. Направление контурного тока и направление обхода контура совпадают. 3. Если в схеме есть источник тока, то надо, считая ток источника за контурный ток, наметить произвольный путь, по которому он будет замыкаться. 4. Составить уравнения по второму закону Кирхгофа для всех независимых контуров. При этом надо учесть падение напряжения от тока источника тока. 5. Определить контурные токи. 6. Определить действительные токи в ветвях.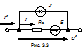
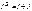 (3.6)
(3.6)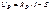 (3.7)
(3.7)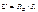 (3.8)
(3.8)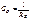
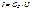 (3.9)
(3.9)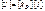 (3.10)
(3.10) (3.11)
(3.11) и
и  причем k равно числу ветвей схемы.
причем k равно числу ветвей схемы.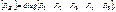 а
а 
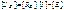
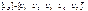


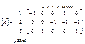 (3.13)
(3.13)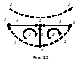
 (3.14)
(3.14)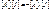 (3.15)
(3.15) (3.16)
(3.16)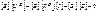 (3.17)
(3.17)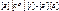
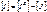 (3.19)
(3.19)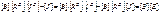 (3.20)
(3.20) или
или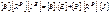 (3.21)
(3.21) (3.22)
(3.22) (3.23)
(3.23)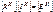 (3.24)
(3.24)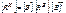 – матрица контурных сопротивлений;
– матрица контурных сопротивлений; 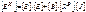 – матрица контурных ЭДС.
– матрица контурных ЭДС.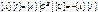 (3.25)
(3.25)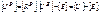 (3.26)
(3.26)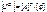 -(3.26) (3.27)
-(3.26) (3.27)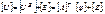 -(3.27). (3.28)
-(3.27). (3.28)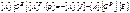 -(3.28) (3.29)
-(3.28) (3.29)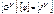 (3.30)
(3.30) , являющийся частью тока I 3 (так как I 2 = 0), который мы найдем по формуле «разброса токов»
, являющийся частью тока I 3 (так как I 2 = 0), который мы найдем по формуле «разброса токов»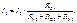 (2.3)
(2.3) (2.4)
(2.4) ;
;  ;
; 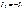 ;
;  . (2.5)
. (2.5)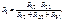 (2.6)
(2.6)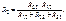
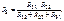 (2.7)
(2.7)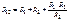 ;
; 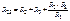 (2.9); (2.10)
(2.9); (2.10)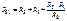 ; (2.11)
; (2.11)