

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
Топ:
Оснащения врачебно-сестринской бригады.
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Функция
Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением (связи) между элементами двух множеств.
I. Понятие функции
1) Зависимости одной переменной от другой называются функциональными зависимостями.
2) Зависимость переменной y от переменной x называется функцией, если каждому значению x
соответствует единственное значение y. При этом используют запись 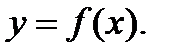
3) Переменную x называют независимой переменной или аргументом, а переменную y –
зависимой переменной. Говорят, что y является функцией от x.
4) Значение y, соответствующее заданному значению x, называют значением функции.
5) Все значения, которые принимает независимая переменная, образуют область определения
функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.
6) Для функции  приняты обозначения:
приняты обозначения: 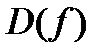 - область определения функции,
- область определения функции, 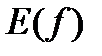 -
-
множество значений функции, 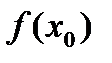 - значение функции в точке
- значение функции в точке  .
.
7) Если функция задана формулой и область определения не указана, то считают, что область
определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
II. Способы задания функции
1) Аналитический способ задания функции – функция задается формулой, позволяющей получить значение зависимой переменной y, подставив конкретной числовое значение аргумента x.
2) Табличный способ задания функции – функция задается таблицей, в верхней строке которой указываются значения независимой переменной x, в нижней – соответствующие значения зависимой переменной y.
| x | -2 | -1 | 0 | 1 | 2 |

| 4 | 1 | 0 | 1 | 4 |
3) Графический способ задания функции – задается график функции.
|
|
III. Свойства функции
Выявление основных свойств функции, позволяющих достаточно наглядно судить о ее поведении, называют исследованием функции.
В стандартную схему исследования функции обычно включают следующие пункты:
1) Область определения функции;
2) Нули функции;
3) Промежутки знакопостоянства;
4) Точки экстремума функции;
5) Промежутки возрастания и убывания (монотонность) функции;
6) Наибольшее и наименьшее значения функции;
7) множество значений функции.
Дадим краткое описание тех понятий, которые включены в схему исследования функции.
1) Область определения – множество значений аргумента, при которых задана функция. Если функция задана формулой и область определения не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
2) Корни (нули) функции – значения аргумента, при которых  , называются корнями (или нулями) функции. Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью ОХ. Для нахождения нулей функции нужно решить уравнение f (x) = 0.
, называются корнями (или нулями) функции. Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью ОХ. Для нахождения нулей функции нужно решить уравнение f (x) = 0.
3) Промежутки знакопостоянства – промежутки, на которых функция сохраняет свой знак
(т.е. остается положительной 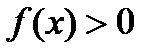 или отрицательной
или отрицательной 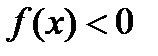 ). для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.
). для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.
4) Точки экстремума – точки, лежащие внутри области определения, в которых функция принимает или самое большое или самое малое значение.
5) Монотонность функции – определяется такими понятиями как возрастающая (или убывающая) функция. Промежутки монотонности – промежутки, на которых функция возрастает (или убывает).
6) Наибольшее и наименьшее значения функции – самое большое или самое малое значение функции по сравнению со всеми возможными.
7) Множество значений – множество чисел, состоящее из всех значений функции.
IV. График функции
Графиком функции  называется множество точек плоскости с координатами (х; у), где х пробегает область определения функции.
называется множество точек плоскости с координатами (х; у), где х пробегает область определения функции.
|
|
VI. Периодичность функции
Функция 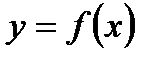 называется периодической, если существует такое число
называется периодической, если существует такое число 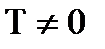 , что для любого
, что для любого
значения из области определения функции выполняется равенство: 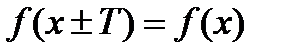 .
.
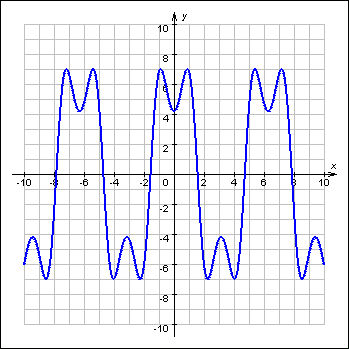
Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π), y = tg x (период равен π) и другие.
Периодические функции: 
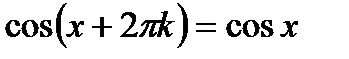
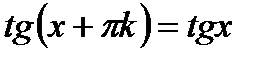

График периодической функции
Отметим, что если f (x) – периодическая функция с периодом T, то функция g (x) = A · f (kx + b), где k ≠ 0 также является периодической с периодом T1= T/ k.
VII. Обратная функция
Пусть задана функция 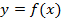 . Она имеет обратную функцию, если из зависимости
. Она имеет обратную функцию, если из зависимости 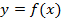 переменную
переменную 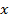 можно однозначно выразить через переменную
можно однозначно выразить через переменную 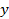 .
.
Для построения графика функции, обратной функции к графику f, надо график исходной функции симметрично отразить относительно прямой 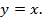
Постоянная функция.
Постоянная функция задается на множестве всех действительных чисел формулой 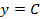 , где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой. Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0, C).
, где C – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой. Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0, C).
Функция
Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением (связи) между элементами двух множеств.
I. Понятие функции
1) Зависимости одной переменной от другой называются функциональными зависимостями.
2) Зависимость переменной y от переменной x называется функцией, если каждому значению x
соответствует единственное значение y. При этом используют запись 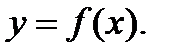
3) Переменную x называют независимой переменной или аргументом, а переменную y –
зависимой переменной. Говорят, что y является функцией от x.
4) Значение y, соответствующее заданному значению x, называют значением функции.
5) Все значения, которые принимает независимая переменная, образуют область определения
|
|
функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.
6) Для функции  приняты обозначения:
приняты обозначения: 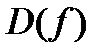 - область определения функции,
- область определения функции, 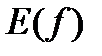 -
-
множество значений функции, 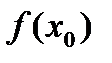 - значение функции в точке
- значение функции в точке  .
.
7) Если функция задана формулой и область определения не указана, то считают, что область
определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
II. Способы задания функции
1) Аналитический способ задания функции – функция задается формулой, позволяющей получить значение зависимой переменной y, подставив конкретной числовое значение аргумента x.
2) Табличный способ задания функции – функция задается таблицей, в верхней строке которой указываются значения независимой переменной x, в нижней – соответствующие значения зависимой переменной y.
| x | -2 | -1 | 0 | 1 | 2 |

| 4 | 1 | 0 | 1 | 4 |
3) Графический способ задания функции – задается график функции.
III. Свойства функции
Выявление основных свойств функции, позволяющих достаточно наглядно судить о ее поведении, называют исследованием функции.
В стандартную схему исследования функции обычно включают следующие пункты:
1) Область определения функции;
2) Нули функции;
3) Промежутки знакопостоянства;
4) Точки экстремума функции;
5) Промежутки возрастания и убывания (монотонность) функции;
6) Наибольшее и наименьшее значения функции;
7) множество значений функции.
Дадим краткое описание тех понятий, которые включены в схему исследования функции.
1) Область определения – множество значений аргумента, при которых задана функция. Если функция задана формулой и область определения не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
2) Корни (нули) функции – значения аргумента, при которых  , называются корнями (или нулями) функции. Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью ОХ. Для нахождения нулей функции нужно решить уравнение f (x) = 0.
, называются корнями (или нулями) функции. Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью ОХ. Для нахождения нулей функции нужно решить уравнение f (x) = 0.
3) Промежутки знакопостоянства – промежутки, на которых функция сохраняет свой знак
|
|
(т.е. остается положительной 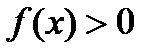 или отрицательной
или отрицательной 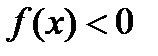 ). для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.
). для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.
4) Точки экстремума – точки, лежащие внутри области определения, в которых функция принимает или самое большое или самое малое значение.
5) Монотонность функции – определяется такими понятиями как возрастающая (или убывающая) функция. Промежутки монотонности – промежутки, на которых функция возрастает (или убывает).
6) Наибольшее и наименьшее значения функции – самое большое или самое малое значение функции по сравнению со всеми возможными.
7) Множество значений – множество чисел, состоящее из всех значений функции.
IV. График функции
Графиком функции  называется множество точек плоскости с координатами (х; у), где х пробегает область определения функции.
называется множество точек плоскости с координатами (х; у), где х пробегает область определения функции.
V. Четность (нечетность) функции
1. Функция 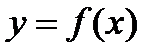 называется четной, если для любого
называется четной, если для любого 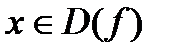 выполняется равенство
выполняется равенство  График четной функции симметричен относительно оси OY.
График четной функции симметричен относительно оси OY.
2. Функция 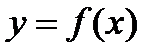 называется нечетной, если для любого
называется нечетной, если для любого 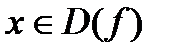 выполняется равенство
выполняется равенство 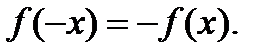 График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.


График четной функции График нечетной функции
Четные функции: 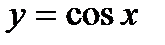 , т.к.
, т.к. 
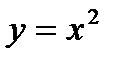 , т.к.
, т.к. 
Нечетные функции: 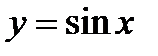 , т. к.
, т. к. 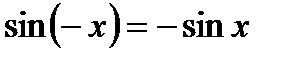
 , т. к.
, т. к. 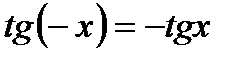
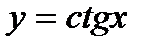 , т. к.
, т. к. 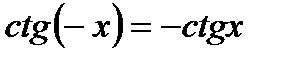
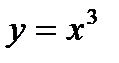 , т.к.
, т.к. 
Исследование функций на четность облегчается следующими утверждениями.
VI. Периодичность функции
Функция 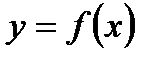 называется периодической, если существует такое число
называется периодической, если существует такое число 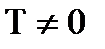 , что для любого
, что для любого
значения из области определения функции выполняется равенство: 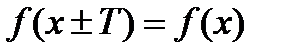 .
.

Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π), y = tg x (период равен π) и другие.
Периодические функции: 
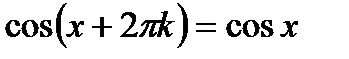
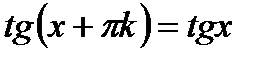

График периодической функции
Отметим, что если f (x) – периодическая функция с периодом T, то функция g (x) = A · f (kx + b), где k ≠ 0 также является периодической с периодом T1= T/ k.
VII. Обратная функция
Пусть задана функция 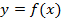 . Она имеет обратную функцию, если из зависимости
. Она имеет обратную функцию, если из зависимости 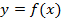 переменную
переменную 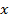 можно однозначно выразить через переменную
можно однозначно выразить через переменную 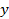 .
.
|
|
Для построения графика функции, обратной функции к графику f, надо график исходной функции симметрично отразить относительно прямой 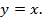
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!