· При изучении основных понятий кредитования, его сущности и его составляющих; информации, представленной в периодической печати, выявились основные направления математики, лежащие в основе кредитования -проценты.
Процентом числа (или от числа) называется сотая часть этого числа. Если число умножить на 100, то получим процентное выражение числа. Процентные вычисления имеют самое широкое (по сравнению с другими дробями) практическое применение в повседневной жизни.
В процентах измеряют изменение цен; количество людей, принявших участие в выборах, содержание примесей в металлах; влажность воздуха; успеваемость учащихся в школе; количество жарких дней в году; точность вычислений; прирост населения; рождаемость и смертность и т.п.
Особенно часто проценты используются в финансовых операциях. Если некоторая величина А вырастает на р% в год (или за другой промежуток времени), то это означает, что она увеличится на величину, равную р% от А, т.е. на 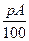 .
.
В результате новое (увеличенное, наращенное) значение А1 станет равным
 =А+
=А+  = А(1+
= А(1+  ).
).
Дальше увеличение величины А связано с тем, от какой величины будет исчисляться процент. Если исчисление будет происходить от первоначальной величины, то говорят об увеличении А по закону простых процентов. Если же от наращенной в течение года величины А1, то говорят, что величина А возрастает по закону сложных процентов.
В случае когда величина А возрастает на одну и ту же величину,
через n лет значение величины А составит  ,
,
то 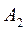 = (А+
= (А+  ) +
) +  = А +
= А + 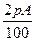 .
.
Через n лет значение величины А составит 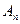 =A(1+
=A(1+  ).
).
Это соотношение называется формулой простых процентов. В случае сложных процентов величина А в течение второго года увеличится на  =
=  А(1+
А(1+  ) и станет равной
) и станет равной
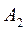 =
=  +
+  = А· (1+
= А· (1+  ) +
) +  А(1+
А(1+  ) =А(1+
) =А(1+  ) (1+
) (1+  ) = А· (1+
) = А· (1+  )².
)².
Через n лет значение величины составит А· (1+  )
)  . Это соотношение называется формулой сложных процентов.
. Это соотношение называется формулой сложных процентов.
Ø Если ежегодная ставка, т.е. величина процента, изменяется, то формула простых процентов примет вид  , а формула сложных процентов вид
, а формула сложных процентов вид  .
.
Ø Основными задачами на части, и проценты являются следующие:
1) нахождение дроби (процентов) от числа;
2) нахождение числа по заданной части (по его процентам);
3) нахождение процентного соотношения нескольких чисел;
4) нахождение наращиваемого капитала (сложные проценты) при заданной процентной ставке (т.е. процент прироста капитала); Основными задачами на части, и проценты являются следующие:
Решение этих задач в общем виде может быть представлено следующим образом:
· р-я часть числа А равна р·А;
· р% от числа А равно А ·  ;
;
· если р-я часть числа равна С, то само число равно 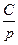 ;
;
· если p% некоторого числа равны С, то это число равно 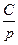 ·100;
·100;
· процентное отношение чисел А и В равно 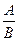 · 100%;
· 100%;
· наращенный капитал за п лет при процентной ставке в р % годовых и и начальном капитале в А р. составит А · ((1+  )
)  -1) р.
-1) р.





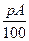 .
.  =А+
=А+  = А(1+
= А(1+  ).
).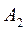 = (А+
= (А+ 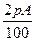 .
. 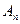 =A(1+
=A(1+  ).
).  =
=  А(1+
А(1+  +
+  = А· (1+
= А· (1+  . Это соотношение называется формулой сложных процентов.
. Это соотношение называется формулой сложных процентов. , а формула сложных процентов вид
, а формула сложных процентов вид  .
.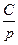 ;
;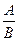 · 100%;
· 100%; -1) р.
-1) р.


