Существуют несколько классов задач, которые удовлетворяют общей задаче динамического программирования. Каждый из классов имеет свой метод решения, обычно представляется наиболее характерной задачей. Простейшие задачи связаны с выбором на каждом шаге одного из двух возможных решений.
Задача о числе траекторий
В прямоугольной таблице, разбитой на клетки (n строк и m столбцов), из левого верхнего угла с координатами (1, 1) нужно переместиться в правый нижний (n, m), перемещаться на каждом шаге можно только вниз или вправо. Составить программу для определения числа всех возможных траекторий. На Рис. 5 показаны некоторые возможные траектории.
Обозначим L(i, j) число траекторий до клетки (i, j). Таким образом, L(n, m) – число возможных траекторий, которое требуется найти.
Рис. 5. Возможные траектории в задаче о числе траекторий
|
| 1
| 2
|
| m -1
| m
|
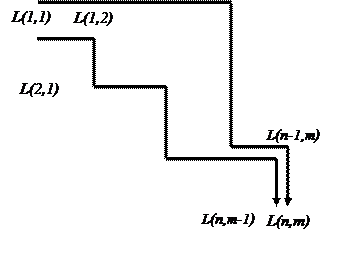 1 1
|
|
|
|
|
|
| 2
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
Все траектории в клетку (n, m) ведут или из (n, m-1), или из (n‑1, m), поэтому их можно сосчитать как сумму этих траекторий:
L(n, m) = L(n-1, m) + L(n, m-1)
Таким образом, решение задачи разделено на решение этой же задачи для меньших значений параметров.
При этом в любую клетку первой строки и первого столбца можно попасть только по одной траектории.
L(i, 1) = L(1, j) = 1
Текст программы, которая подсчитывает число траекторий для произвольных n и m (Рис. 6), и результат ее работы (Рис. 7) представлены ниже.
Рис. 6. Программа подсчета числа траекторий
# include <iostream>
using namespace std;
// Подсчет числа траекторий для прямоугольника n x m
int L(int n, int m)
{
return (n==1 || m==1)? 1: L(n-1,m) + L(n,m-1);
}
// Подсчет числа траекторий
int main ()
{
cout << L(10,10) << " " << L(15,15) << "\n";
return 0;
}
Рис. 7. Листинг программы подсчета числа траекторий
48620 40116600
Задание: составив программу, вычислить число траекторий для (8, 3).
Таким образом, если по какой-то причине нужно перебрать все траектории для выбора в каком-то смысле наилучшей, то уже для прямоугольника 15 x 15 объем вычислений определен обработкой 40116600 траекторий. Программа (Рис. 6) подсчитывала число траекторий около 6 секунд. После изменения программы подсчета, как это показано на Рис. 8, получается таблица значений (Таблица 1).
Большой объем вычислений можно объяснить многократным выполнением одних и тех же операций. Например, L (i, j) нужно вычислять и при вычислении L (i +1, j), и при вычислении L (i, j +1). Однако, можно поступить и по-другому: если мы запомним найденное значение L (i, j), то второй раз его находить не будем, это и представляет основную идею методов динамического программирования.
Рис. 8. Программа для построения зависимости числа траекторий от размера таблицы
// Таблица числа траекторий
int main ()
{
int n, m;
for (n = 1; n <= 11; n++)
{
cout << "\n";
for (m = 1; m <= 11; m++)
cout << L(n, m) << "\t";
}
return 0;
}
Таблица 1. Зависимость числа траекторий от размера таблицы
| n/m
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
|
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
| 2
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
|
| 3
| 1
| 3
| 6
| 10
| 15
| 21
| 28
| 36
| 45
| 55
| 66
|
| 4
| 1
| 4
| 10
| 20
| 35
| 56
| 84
| 120
| 165
| 220
| 286
|
| 5
| 1
| 5
| 15
| 35
| 70
| 126
| 210
| 330
| 495
| 715
| 1001
|
| 6
| 1
| 6
| 21
| 56
| 126
| 252
| 462
| 792
| 1287
| 2002
| 3003
|
| 7
| 1
| 7
| 28
| 84
| 210
| 462
| 924
| 1716
| 3003
| 5005
| 8008
|
| 8
| 1
| 8
| 36
| 120
| 330
| 792
| 1716
| 3432
| 6435
| 11440
| 19448
|
| 9
| 1
| 9
| 45
| 165
| 495
| 1287
| 3003
| 6435
| 12870
| 24310
| 43758
|
| 10
| 1
| 10
| 55
| 220
| 715
| 2002
| 5005
| 11440
| 24310
| 48620
| 92378
|
| 11
| 1
| 11
| 66
| 286
| 1001
| 3003
| 8008
| 19448
| 43758
| 92378
| 184756
|
Мы могли заполнить таблицу, приведенную выше, начиная с угла (1,1) по тому же рекуррентному соотношению:
L(n, m) = L(n-1, m) + L(n, m-1)
Ход такого вычисления называется обратным (нисходящим). Программа, которая выполняет такие вычисления, представлена на Рис. 9, ее листинг совпадает с представленным на Рис. 7. Она использует промежуточную память размером (n+1) ´ (m+1), однако выполняется очень быстро.
Рис. 9. Программа подсчета числа траекторий обратным ходом
#include <iostream>
using namespace std;
// Обратный ход подсчета числа траекторий
# define A(i,j) a[(i)*m+(j)]
int din (int n, int m)
{
int i,j, *a = new int [(n+1)*(m+1)];
for (i = 1; i<=n; i++)
for (j = 1; j<=m; j++)
A(i,j) = ((i==1)||(j==1))? 1: A(i-1,j) + A(i,j-1);
i = A(n, m);
free (a);
return i;
}
// Подсчет числа траекторий
int main ()
{
cout << din(10,10) << " " << din(15,15);
return 0;
}
Например, для вычисления числа траекторий L(8,3) будут получены только значения в затененной части (Таблица 1).



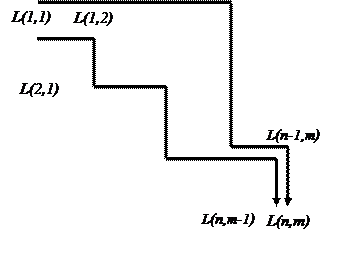 1
1


