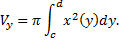Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов.
Несобственные интегралы 1-го рода
Пусть  определена на
определена на  и интегрируема на любом отрезке вида
и интегрируема на любом отрезке вида  . Зафиксируем
. Зафиксируем 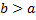 и рассмотрим определенный интеграл
и рассмотрим определенный интеграл  .
.
Опр. Несобственным интегралом 1 рода функции  от
от  до
до  называется предел при
называется предел при  определенного интеграла от
определенного интеграла от  до
до  :
:


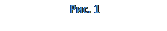
 Если
Если  конечный предел
конечный предел  , то несобственный интеграл от
, то несобственный интеграл от  до
до  называется сходящимся, в противном случае (т.е. если предел
называется сходящимся, в противном случае (т.е. если предел  равен
равен  или не существует) – расходящимся.
или не существует) – расходящимся.
Геометрический смысл – площадь бесконечной фигуры, ограниченной линиями 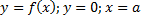 (см. рис. 8).
(см. рис. 8).

 Аналогично для функции
Аналогично для функции  , определенной на
, определенной на  по определению
по определению
 (см. рис. 9).
(см. рис. 9).
Свойство линейности.
Если  ,
, 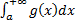 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы

 .
.
Аналогично для  .
.
Вычисление несобственного интеграла 1-го рода.
Пусть  – первообразная для
– первообразная для  на
на  , тогда
, тогда

Таким образом,  сходится
сходится 
 конечный предел первообразной
конечный предел первообразной 
Примеры.
 ,
, 

Рис. 10


Рис. 11
1. 

Рис. 12
2. 


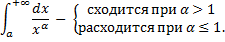

Исследование несобственных интегралов 1-го рода на сходимость.
 Признаки сходимости:
Признаки сходимости:
1. Признак сравнения.
Пусть 

a. Если  сходится, то
сходится, то  также сходится (см. рис. 13).
также сходится (см. рис. 13).
b. Если  расходится, то
расходится, то  также расходится.
также расходится.
2. Предельный признак сравнения:
пусть для 
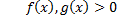 и
и  при
при  , т.е.
, т.е.  .
.
Тогда  и
и  оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
3. Если сходится  , то сходится и
, то сходится и  (обратное неверно!).
(обратное неверно!).
В качестве «образцов» интегралов для сравнения обычно используются интегралы
 (a>0).
(a>0).
Примеры.
1.  .
.
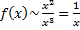 при
при 
 расходится
расходится  исходный интеграл расходится по предельному признаку.
исходный интеграл расходится по предельному признаку.

При 
 ;
;  ;
;  ,
,
 ;
;  интеграл сходится по предельному признаку.
интеграл сходится по предельному признаку.
3. 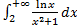
Т.к. при 
 (логарифм растет медленней степенной функции), то
(логарифм растет медленней степенной функции), то  исходный интеграл сходится по признаку сравнения.
исходный интеграл сходится по признаку сравнения.
 .
.
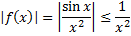
 – сходится
– сходится  сходится по признаку 3.
сходится по признаку 3.
Несобственные интегралы 2-го рода

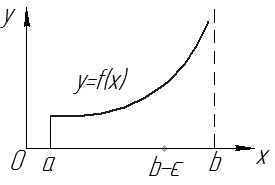 Пусть
Пусть  непрерывна на
непрерывна на  , но не ограничена в левой окрестности точки
, но не ограничена в левой окрестности точки  . Определенный интеграл
. Определенный интеграл  не существует, т.к.
не существует, т.к.  – неограниченная. Рассмотрим
– неограниченная. Рассмотрим  . Т.к.
. Т.к.  непрерывна на
непрерывна на  , то
, то  – определенный интеграл.
– определенный интеграл.
Опр. Несобственным интегралом 2 рода по 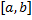 от функции
от функции  , неограниченной в окрестности точки
, неограниченной в окрестности точки  , называется предел
, называется предел

Если существует конечный предел (1.8.2), то несобственный интеграл 2-го рода называется сходящимся, в противном случае – расходящимся.
Геометрический смысл:
при 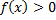 – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 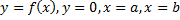 (см. рис. 15).
(см. рис. 15).
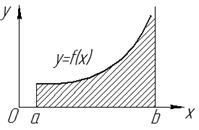
Рис. 15
 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой  .
.
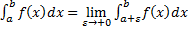 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 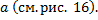

Рис. 16
Свойство линейности.
Если  ,
,  сходятся, то сходятся интегралы
сходятся, то сходятся интегралы

 .
.
Вычисление несобственного интеграла 2-го рода.
Случай функции с особой точкой 

 – первообразная для
– первообразная для 
Таким образом,  сходится
сходится 
 конечный предел первообразной
конечный предел первообразной  .
.
Примеры.



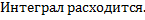
Рассмотрим интегралы

Рассмотрим случай интеграла с особой точкой в левом конце отрезка:
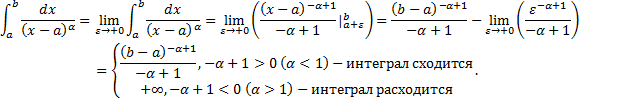
Случай 

Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом

 имеет при
имеет при 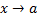 порядок роста
порядок роста  относительно
относительно  ).
).
Примеры несобственных интегралов с несколькими особыми точками
1. 
Исходный интеграл сходится, если сходятся оба интеграла в правой части:
a.  .
.

b. 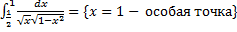 .
.

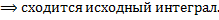
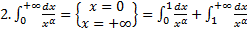 .
.
(несобственный интеграл 2-го рода  + несобственный интеграл 1-го рода
+ несобственный интеграл 1-го рода  ).
).
a.  – сходится при
– сходится при 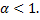
b.  – сходится при
– сходится при 
Значит,  расходится для любого
расходится для любого  .
.
 .
.
a. 
При 
b. 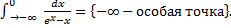
При  .
.
Таким образом исходный интеграл расходится.
Объемы тел вращения.

Рис. 26
Фигура, ограниченная линиями  , вращается вокруг оси
, вращается вокруг оси 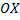 (см. рис. 26).
(см. рис. 26).
Найдем объем 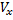 тела вращения. Зафиксируем
тела вращения. Зафиксируем  . Сечение тела плоскостью
. Сечение тела плоскостью  – круг радиуса
– круг радиуса 
 . Тогда
. Тогда

Ту же фигуру вращаем вокруг оси 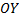 (см. рис. 27).
(см. рис. 27).
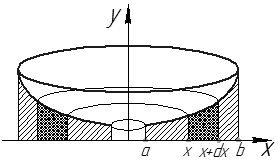
Рис. 27
Рассмотрим малый отрезок  , где
, где  . При вращении соответствующей части фигуры получаем тело объема
. При вращении соответствующей части фигуры получаем тело объема  , где
, где 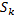 – площадь кольца радиусов
– площадь кольца радиусов  и
и  соответственно:
соответственно:
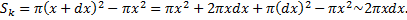
Тогда

Суммируя по тонким "слоям", получим
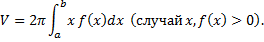
Общий случай:

Таким образом получаем для вращения фигуры, ограниченной линиями  , имеем
, имеем

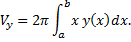
При вращении фигуры, ограниченной линиями 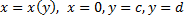 (см. рис. 28).
(см. рис. 28).

Рис. 28

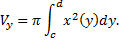
Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов.



 определена на
определена на  и интегрируема на любом отрезке вида
и интегрируема на любом отрезке вида  . Зафиксируем
. Зафиксируем  и рассмотрим определенный интеграл
и рассмотрим определенный интеграл  .
. до
до  называется предел при
называется предел при  определенного интеграла от
определенного интеграла от  :
:

 Если
Если  конечный предел
конечный предел  , то несобственный интеграл от
, то несобственный интеграл от  или не существует) – расходящимся.
или не существует) – расходящимся. (см. рис. 8).
(см. рис. 8).

 по определению
по определению (см. рис. 9).
(см. рис. 9). ,
, 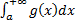 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы
 .
. – первообразная для
– первообразная для  на
на  , тогда
, тогда


 ,
, 








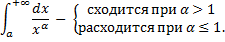

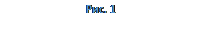
 Признаки сходимости:
Признаки сходимости:

 сходится, то
сходится, то  также сходится (см. рис. 13).
также сходится (см. рис. 13).
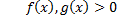 и
и  при
при  , т.е.
, т.е.  .
. , то сходится и
, то сходится и  (a>0).
(a>0). .
.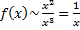 при
при 
 расходится
расходится  исходный интеграл расходится по предельному признаку.
исходный интеграл расходится по предельному признаку.
 ;
;  ;
;  ,
, ;
;  интеграл сходится по предельному признаку.
интеграл сходится по предельному признаку.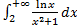

 (логарифм растет медленней степенной функции), то
(логарифм растет медленней степенной функции), то  исходный интеграл сходится по признаку сравнения.
исходный интеграл сходится по признаку сравнения. .
.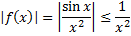
 – сходится
– сходится  сходится по признаку 3.
сходится по признаку 3.
 Пусть
Пусть  , но не ограничена в левой окрестности точки
, но не ограничена в левой окрестности точки  . Т.к.
. Т.к.  , то
, то  – определенный интеграл.
– определенный интеграл.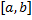 от функции
от функции 
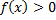 – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 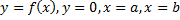 (см. рис. 15).
(см. рис. 15).
 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 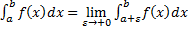 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 

 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы


 – первообразная для
– первообразная для  .
.



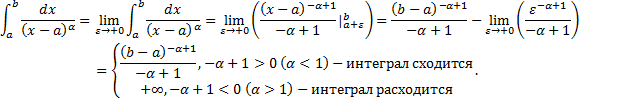



 имеет при
имеет при  порядок роста
порядок роста  относительно
относительно  ).
).
 .
.
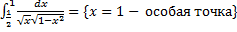 .
.
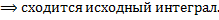
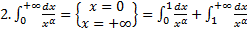 .
. + несобственный интеграл 1-го рода
+ несобственный интеграл 1-го рода  ).
). – сходится при
– сходится при 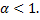
 – сходится при
– сходится при 
 расходится для любого
расходится для любого  .
.

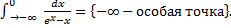
 .
.
 , вращается вокруг оси
, вращается вокруг оси  (см. рис. 26).
(см. рис. 26). тела вращения. Зафиксируем
тела вращения. Зафиксируем  . Сечение тела плоскостью
. Сечение тела плоскостью  – круг радиуса
– круг радиуса  . Тогда
. Тогда
 (см. рис. 27).
(см. рис. 27).
 , где
, где  , где
, где 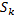 – площадь кольца радиусов
– площадь кольца радиусов  и
и  соответственно:
соответственно: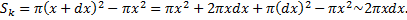

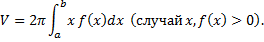

 , имеем
, имеем
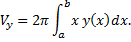
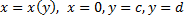 (см. рис. 28).
(см. рис. 28).