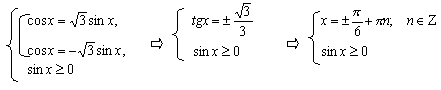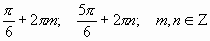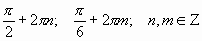При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа – число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.
1. Алгебраические уравнения относительно одной из тригонометрических функций.
Необходимо произвести замену неизвестных таким образом, чтобы тригонометрическое уравнение преобразовалось в «удобное» для решения алгебраическое уравнение.
Примеры
1) Решить уравнение 2sin2 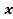 + 3sin
+ 3sin 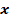 —2 = 0.
—2 = 0.
Это уравнение является квадратным относительно sin 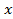 .
.
Его корни: sin 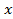 =
=  , sin
, sin 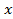 =—2. Второе из полученных простейших уравнений не имеет решений, так как Isin
=—2. Второе из полученных простейших уравнений не имеет решений, так как Isin 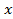 l
l 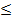 1, решения первого можно записать так:
1, решения первого можно записать так:
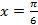 +2k
+2k 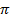 ,
, 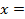 π
π 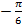 + 2k
+ 2k 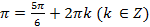
Если в уравнении встречаются разные тригонометрические функции, то надо заменить их все на какую-нибудь одну, используя тригонометрические тождества.
2) Решить уравнение 2sin 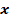 + cos
+ cos 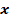 = 2.
= 2.
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используем формулы, выражающие синус и косинус через тангенс половинного угла:
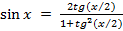 и
и 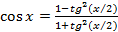 .
.
Делая замену, получаем уравнение относительно 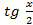 :
: 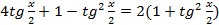 .
.
Квадратное уравнение 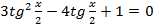 имеет корни
имеет корни 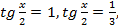 откуда
откуда
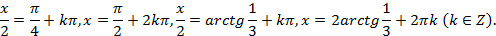
Это же уравнение можно решить другим способом, вводя вспомогательный угол:
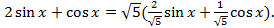
Пусть 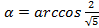 . Тогда можно продолжить преобразование:
. Тогда можно продолжить преобразование: 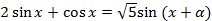 . Получаем простейшее уравнение
. Получаем простейшее уравнение 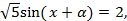 т. е.
т. е. 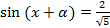 , откуда
, откуда 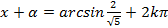 , или
, или 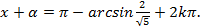
Ответ получился в другом виде, однако можно проверить, что решения на самом деле совпадают.
2. Понижение порядка уравнения.
Формулы удвоения 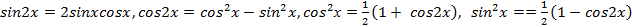 позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры
1) Решить уравнение 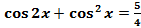 .
.
Можно заменить cos2 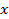 на 2cos2
на 2cos2 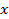 —1 и получить квадратное уравнение относительно cos
—1 и получить квадратное уравнение относительно cos 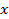 , но проще заменить
, но проще заменить 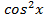 на
на 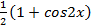 и получить линейное уравнение относительно
и получить линейное уравнение относительно 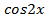 .
.
2) Решить уравнение 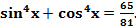
Подставляя вместо 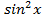 ,
, 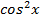 их выражения через
их выражения через 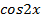 , получаем:
, получаем:
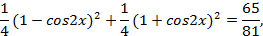
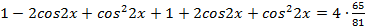 ,
,
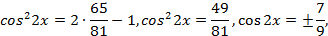
2 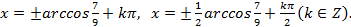
3. Использование тригонометрических формул сложения и следствий из них.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы сложения.
Примеры
1) Решить уравнение 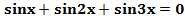 .
.
Сложим два крайних слагаемых: 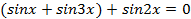 , откуда
, откуда 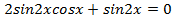 ,
, 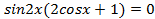 . Тогда
. Тогда 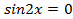 ,
, 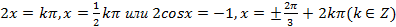 .
.
2) Решить уравнение 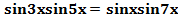 .
.
Преобразуем произведение синусов в сумму: 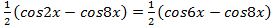 ,
,
откуда 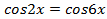 . Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать
. Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать 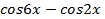 в произведение. Удобнее воспользоваться условием равенства косинусов двух углов
в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 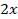 и
и 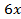 :
: 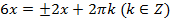 .
.
Получаем два уравнения: 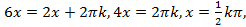
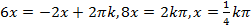 .
.
Здесь решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче: 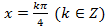 .
.
4. Однородные уравнения.
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решить, выполнив деление на старшую степень синуса (или косинуса).
Так как 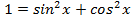 , то постоянные слагаемые можно считать членами второй степени.
, то постоянные слагаемые можно считать членами второй степени.
Пример: 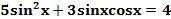 .
.
Заменяя 4 на 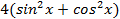 ,получаем:
,получаем: 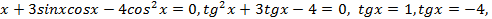
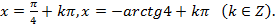
5. Переход к половинному углу
Рассмотрим этот метод на примере:
Пример 6. Решить уравнение: 3 sin x – 5 cos x = 7.
Решение.
6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =
= 7 sin ² (x / 2) + 7 cos ² (x / 2),
2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0,
tg ² (x / 2) – 3 tg (x / 2) + 6 = 0,
6. Введение вспомогательного угла
Рассмотрим уравнение вида:
a sin x + b cos x = c,
где a, b, c – коэффициенты; x – неизвестное.
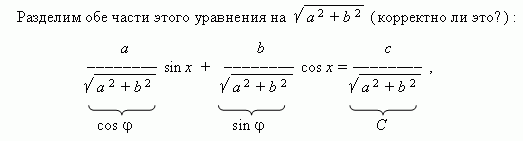
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos 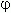 и sin
и sin 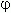 (здесь
(здесь 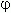 - так называемый вспомогательный угол), и наше уравнение принимает вид:
- так называемый вспомогательный угол), и наше уравнение принимает вид:
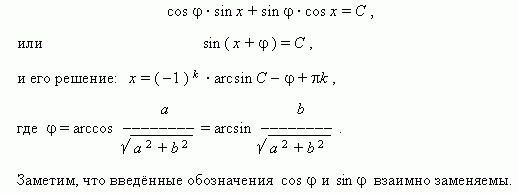
Пример. Решить уравнение: 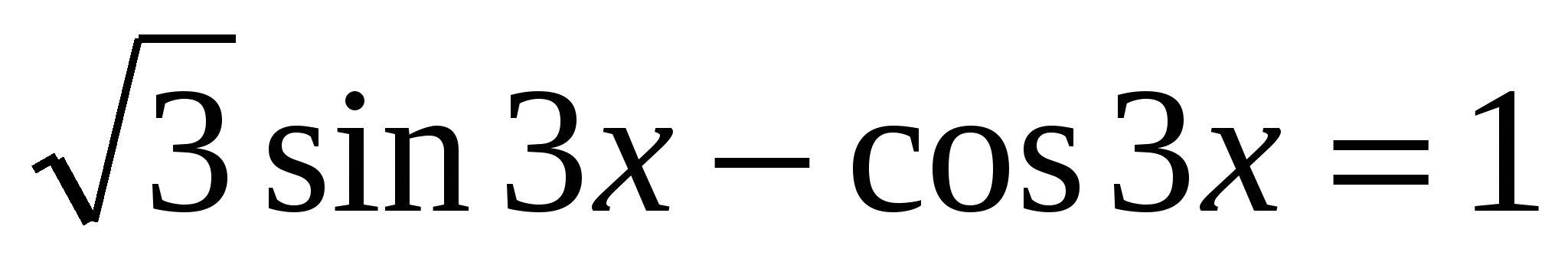
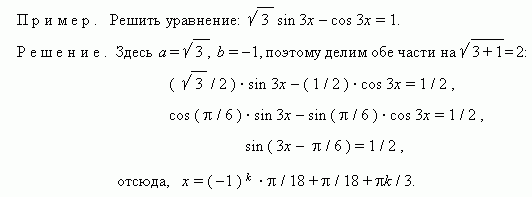
Приемы решения тригонометрических уравнений, требующих искусственных преобразований.
1. Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию.
Пример. Решите уравнение 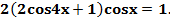
Решение. Раскроем скобки и преобразуем произведение
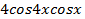 в сумму:
в сумму: 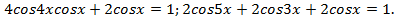
Умножим обе части уравнения на 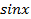 . Заметим, что
. Заметим, что 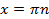 ,
,  не является решением данного уравнения.
не является решением данного уравнения. 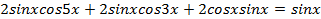 . Преобразуем левую часть уравнения:
. Преобразуем левую часть уравнения:
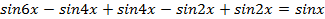 ;
; 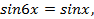 или
или 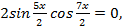 тогда
тогда
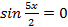 или
или 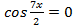 , т.е.
, т.е. 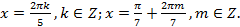
Исключим из найденных серий корни вида 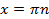 ,
,  :
:
а) 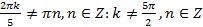 . Ясно, что
. Ясно, что 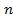 - четное число, т.е.
- четное число, т.е. 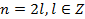 , а потому
, а потому 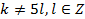 .
.
б) 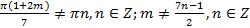 .Tax как
.Tax как 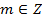 , то
, то 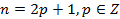 ,но тогда
,но тогда 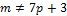 ,
, 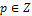 .
.
Ответ: 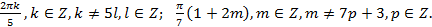
2. Прибавление к обеим частям уравнения одного и того же числа, одной и той же тригонометрической функции.
Пример. Решите уравнение 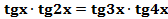 .
.
Решение. Область определения уравнения задается неравенствами:
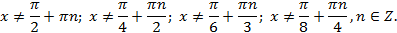
При6авим к обеим частям уравнения по единице. 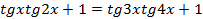 ;
;
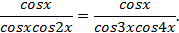
Разделим обе части уравнения на 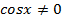 и после преобразований получим.
и после преобразований получим.
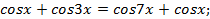
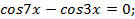
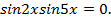
Тогда 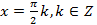 или
или 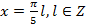 .
.
Из первой серии корней области определения принадлежит только  ,
, 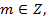 но это серия корней содержится в серии
но это серия корней содержится в серии 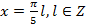 . Нетрудно убедиться, что
. Нетрудно убедиться, что 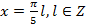 входит в область определения. Например:
входит в область определения. Например: 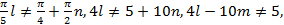 что верно, поскольку левая часть - число четное, а правая - нечетное.
что верно, поскольку левая часть - число четное, а правая - нечетное.
Ответ: 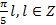 .
.
3. Тождественные преобразования одной из частей уравнения.
Пример. Решите уравнение 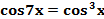 .
.
Решение. Преобразуем левую часть уравнения:
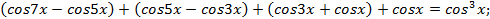
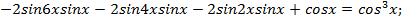
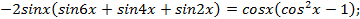
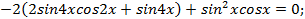
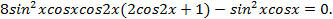
Откуда 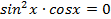 , тогда
, тогда 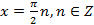 или
или 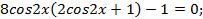
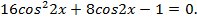
Легко видеть, что 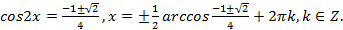
Ответ: 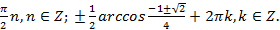
4. Использование свойств пропорции.
Необходимо помнить, что применение равенств
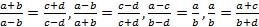 и т. д. приводит к изменению области определения уравнения. Так, у пропорции
и т. д. приводит к изменению области определения уравнения. Так, у пропорции 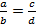 существует ограничение:
существует ограничение: 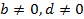 , а у пропорции
, а у пропорции 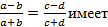 место другое ограничение:
место другое ограничение: 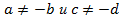 .
.
Пример. Решите уравнение 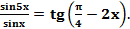
Решение. Применяя формулу тангенса разности, получим уравнение: 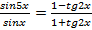 . Используем свойство пропорции:
. Используем свойство пропорции: 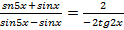 ;
; 
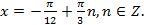 Область определения исходного уравнения:
Область определения исходного уравнения: 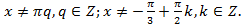
В ходе решения произошло сужение области определения, добавились новые, ограничения: 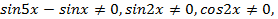 откуда
откуда 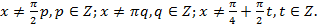
Проверим, удовлетворяют ли исходному уравнению значения
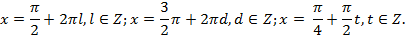
а) 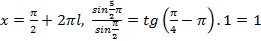 -верное равенство,
-верное равенство,
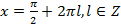 - решение исходного уравнения.
- решение исходного уравнения.
б) 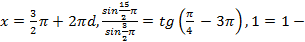 верное равенство.
верное равенство.
в) 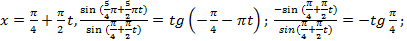 -1
-1 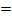 -1 - верное равенство, Ответ:
-1 - верное равенство, Ответ: 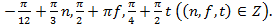
5. Решение тригонометрических уравнений методом экстремальных значений.
При решении некоторых тригонометрических уравнений бывает удобно использовать ограниченность функций, 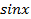 и
и 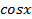 . Покажем это на конкретных примерах.
. Покажем это на конкретных примерах.
Пример 1. Решите уравнение 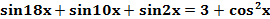 .
.
Решение. Так как 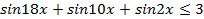 , то
, то 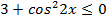 ,
, 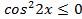 , откуда
, откуда 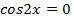 и возможные корни данного уравнения
и возможные корни данного уравнения 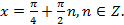 Подставив эти значения в левую часть уравнения, получим
Подставив эти значения в левую часть уравнения, получим 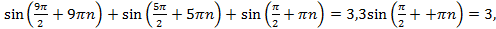 а последнее равенство возможно только при
а последнее равенство возможно только при 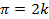 .
.
Следовательно, 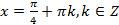 - решение данного уравнения.
- решение данного уравнения.
Ответ: 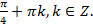
Пример 2. Решите уравнение 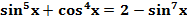 .
.
Решение. Легко видеть, что  и
и 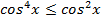 . Следовательно,
. Следовательно, 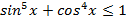 , но тогда
, но тогда 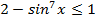 ,
,  , откуда
, откуда  ,
, 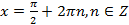 — возможные корни данного
— возможные корни данного
уравнения. Подстановка 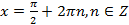 в данное уравнение показывает, что эти числа действительно являются его корнями.
в данное уравнение показывает, что эти числа действительно являются его корнями.
Ответ: 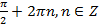 .
.
6. Уравнения, содержащие модуль функции и корень четной степени
Пример 1.


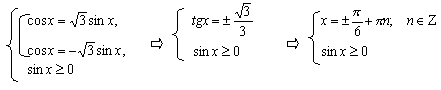
При отборе корней нет надобности решать неравенство, достаточно вынести корни на тригонометрический круг и выбрать нужные.
Ответ: 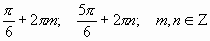
Пример 2.

Решение: Учитывая ОДЗ функций, получим:
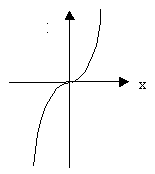
Ответ: 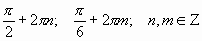



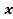 + 3sin
+ 3sin 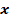 —2 = 0.
—2 = 0.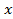 .
. , sin
, sin 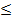 1, решения первого можно записать так:
1, решения первого можно записать так: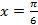 +2k
+2k 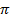 ,
, 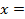 π
π 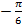 + 2k
+ 2k 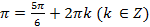
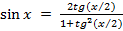 и
и 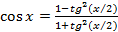 .
.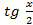 :
: 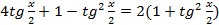 .
.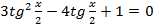 имеет корни
имеет корни 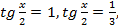 откуда
откуда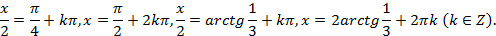
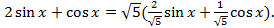
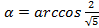 . Тогда можно продолжить преобразование:
. Тогда можно продолжить преобразование: 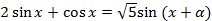 . Получаем простейшее уравнение
. Получаем простейшее уравнение 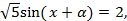 т. е.
т. е. 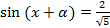 , откуда
, откуда 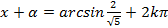 , или
, или 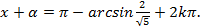
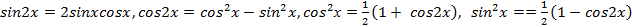 позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
позволяют квадраты синуса, косинуса и их произведения заменять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.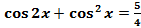 .
.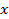 на 2cos2
на 2cos2 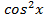 на
на 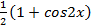 и получить линейное уравнение относительно
и получить линейное уравнение относительно 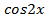 .
.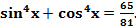
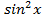 ,
, 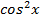 их выражения через
их выражения через 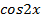 , получаем:
, получаем: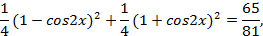
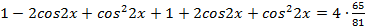 ,
,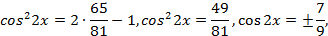
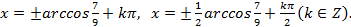
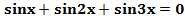 .
.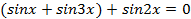 , откуда
, откуда 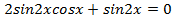 ,
, 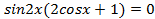 . Тогда
. Тогда 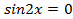 ,
, 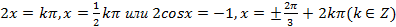 .
.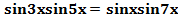 .
.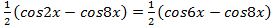 ,
,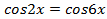 . Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать
. Полученное уравнение можно решить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать 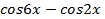 в произведение. Удобнее воспользоваться условием равенства косинусов двух углов
в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 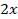 и
и 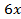 :
: 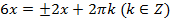 .
.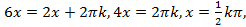
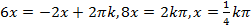 .
.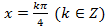 .
.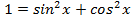 , то постоянные слагаемые можно считать членами второй степени.
, то постоянные слагаемые можно считать членами второй степени.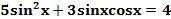 .
.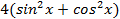 ,получаем:
,получаем: 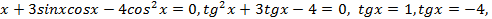
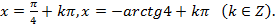
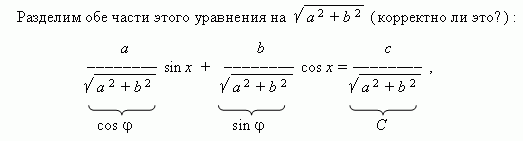
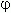 и sin
и sin 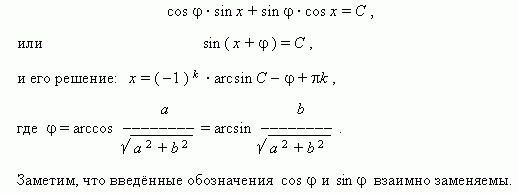
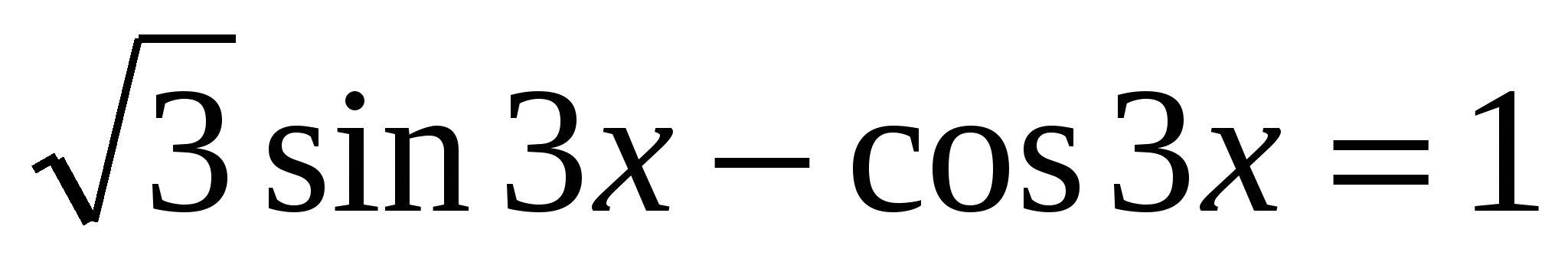
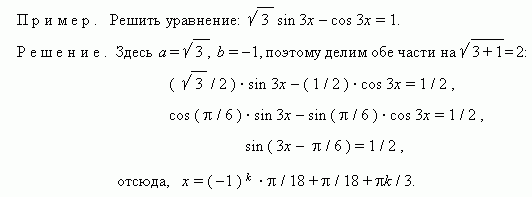
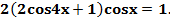
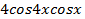 в сумму:
в сумму: 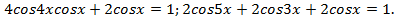
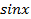 . Заметим, что
. Заметим, что 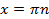 ,
,  не является решением данного уравнения.
не является решением данного уравнения. 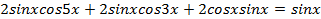 . Преобразуем левую часть уравнения:
. Преобразуем левую часть уравнения: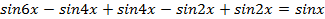 ;
; 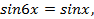 или
или 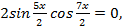 тогда
тогда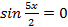 или
или 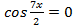 , т.е.
, т.е. 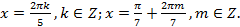
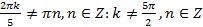 . Ясно, что
. Ясно, что 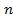 - четное число, т.е.
- четное число, т.е. 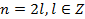 , а потому
, а потому 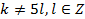 .
.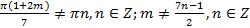 .Tax как
.Tax как 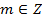 , то
, то 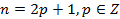 ,но тогда
,но тогда 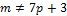 ,
, 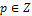 .
.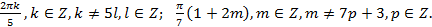
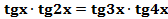 .
.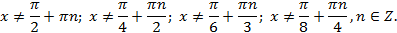
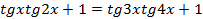 ;
;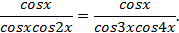
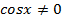 и после преобразований получим.
и после преобразований получим.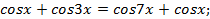
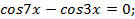
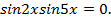
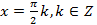 или
или 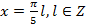 .
. ,
, 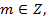 но это серия корней содержится в серии
но это серия корней содержится в серии 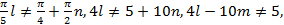 что верно, поскольку левая часть - число четное, а правая - нечетное.
что верно, поскольку левая часть - число четное, а правая - нечетное.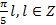 .
.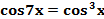 .
.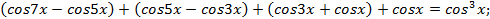
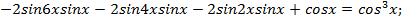
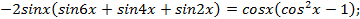
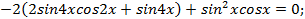
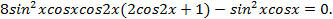
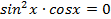 , тогда
, тогда 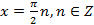 или
или 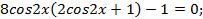
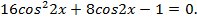
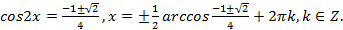
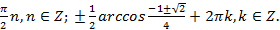
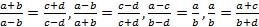 и т. д. приводит к изменению области определения уравнения. Так, у пропорции
и т. д. приводит к изменению области определения уравнения. Так, у пропорции 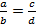 существует ограничение:
существует ограничение: 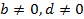 , а у пропорции
, а у пропорции 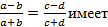 место другое ограничение:
место другое ограничение: 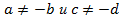 .
.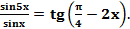
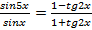 . Используем свойство пропорции:
. Используем свойство пропорции: 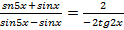 ;
; 
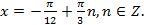 Область определения исходного уравнения:
Область определения исходного уравнения: 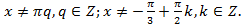
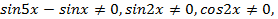 откуда
откуда 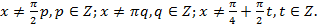
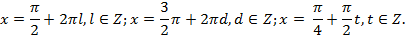
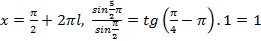 -верное равенство,
-верное равенство,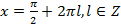 - решение исходного уравнения.
- решение исходного уравнения.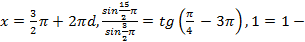 верное равенство.
верное равенство.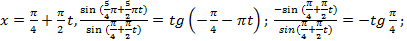 -1
-1 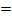 -1 - верное равенство, Ответ:
-1 - верное равенство, Ответ: 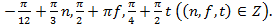
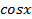 . Покажем это на конкретных примерах.
. Покажем это на конкретных примерах.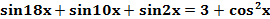 .
.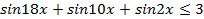 , то
, то 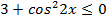 ,
, 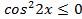 , откуда
, откуда 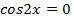 и возможные корни данного уравнения
и возможные корни данного уравнения 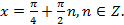 Подставив эти значения в левую часть уравнения, получим
Подставив эти значения в левую часть уравнения, получим 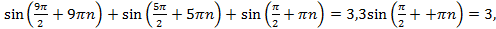 а последнее равенство возможно только при
а последнее равенство возможно только при 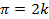 .
.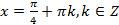 - решение данного уравнения.
- решение данного уравнения.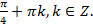
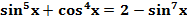 .
. и
и 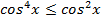 . Следовательно,
. Следовательно, 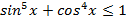 , но тогда
, но тогда 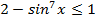 ,
,  , откуда
, откуда  ,
, 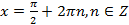 — возможные корни данного
— возможные корни данного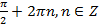 .
.