Если 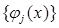 являются степенями {1, х, х2, …, хn}, то говорят об алгебраической интерполяции, а функцию
являются степенями {1, х, х2, …, хn}, то говорят об алгебраической интерполяции, а функцию  называют интерполяционным полиномом и обозначим как:
называют интерполяционным полиномом и обозначим как:
 (4)
(4)
Если
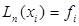 (
( ) (5),
) (5),
то можно построить интерполяционный полином степени n и притом только один.
Найдем интерполяционный полином из вида (4). В это время, на основе (5), для нахождения неопределённых коэффициентов используем систему линейных уравнений:
a0x0 + a1x0 + a2x02 + …+ anx0n= f0,
a0x0 + a1x1 + a2x12 + …+ anx1n= f1, (6)
………………………………………………………….
a0x0 + a1xn + a2xn2 + …+ anxnn= fn,
В этом случае определитель системы линейных алгебраических уравнений выглядит так:
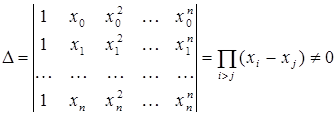 .
.
Этот определитель является определителем Вандермонда и отличен от нуля в случае, когда все узлы xi различны. Поскольку матрица системы невырождена, то решение системы существует и единственно.
Единственность интерполяционного полинома можно доказать следующим способом. Предположим, что есть два интерполяционных полинома
Ln и Pn ÎHn [1] : Ln ≠ Pn.
Из (5): Ln(xi) - Pn(xi) º0 и Ln(xi) º Pn(xi) ( ).
).
так, выходит противоречие. Единственность установлена. А так как полином единственный, то у соответствующей системы линейных алгебраических уравнений есть только одно решение.
Интерполяционный полином Лагранжа
Сейчас перед нами задача, которая состоит из нахождения такого многочлена, степени n, который совпадает с заданной f(x) в точках x1, x2, …, xn Î [a,b], т.е. чтобы выполнялось равенство
(6) f(xj)=Ln(xj) ( ).
).
Чтобы решить эту задачу, введем многочлены степени n, которые в точках при i≠j равны нулю, а в точке при i=j равны единице. Очевидно, что:
(7) fjÎHn, fj(x)=Aj(x-x0)(x-x1)…(x-xj-1)(x-xj+1)…(x-xn)=  ,
,
где постоянная А находится из условия fj(xj)=1, тогда

Таким образом, получаем, что
fj(x) 
Получаем, что поставленную задачу решает многочлен
(8) 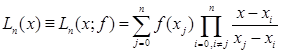
Многочлен (8) называется интерполяционным многочленом Лагранжа.
Задача 1.
Пусть задана интерполяционная таблица:
| i
| 0
| 1
| 2
| 3
|

| 0
| 2
| 3
| 5
|

| 1
| 3
| 2
| 5
|
Построить интерполяционный полином Лагранжа.
Решение. Из (8) следует:

Задача 2.
Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой, проходящей через точки Р0(х0, у0) и Р1(х1, у1), если х0=-1, у0=-3, х1=2, у1=4.
Решение. В данном случае многочлен Лагранжа примет вид
 .
.
Уравнение искомой прямой есть  .
.
Про погрешность полинома
По строению  (
( ). Но, в общем, это не так и
). Но, в общем, это не так и  (
( ,
,  ), так как интерполирование предполагает приближенное нахождение:
), так как интерполирование предполагает приближенное нахождение:
 (
(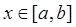 )
)
И в связи с этим необходимо говорить о погрешности интерполирования. Заранее сказав,  разность этого выражения нужно найти.
разность этого выражения нужно найти.
Замечание 1.
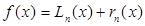 (
( )
)
чем постоянно записывать равенство, слагаемое  называют остаточным членом (или погрешность интерполяции).
называют остаточным членом (или погрешность интерполяции).
Теорема 1.
Если  [a,b] [2]
[a,b] [2]
(9)  (
( ,
,  ), где
), где 
 [a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций.
[a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций.
 [a,b] ó
[a,b] ó  [a,b];
[a,b];

Берем любую точку и зафиксируем ее ( ,
,  ), рассмотрим вспомогательную функцию:
), рассмотрим вспомогательную функцию:
(10) 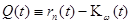 , (
, ( ).
).
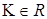 - свободный параметр, который открыто объясняет
- свободный параметр, который открыто объясняет  (
( ).
).
Значение  берем проходящим через равенство
берем проходящим через равенство 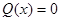 . В это время концы
. В это время концы  , будучи точками промежутка, можно использовать теорему Ролля.
, будучи точками промежутка, можно использовать теорему Ролля.
Существует  :
:  (
( )
)
Сейчас для этой теоремы берем точки  :
:
Существует  :
:  (
( )
)
Когда закончим этот процесс, то получим следующее:
$  :
: 
Итак, при t = x из (10) вытекает (9). Что и требовалось доказать.
Следствие 1:
Пусть  .
.
В то время  (
( ); над ними:
); над ними:  .
.
Задача 3:

С помощью узлов  построить полином
построить полином 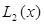 для этой функции, при:
для этой функции, при:
1)  . Оценить погрешность полинома;
. Оценить погрешность полинома;
2) в [a,b] найти максимальную погрешность полинома.
Решение: 



1) На основании Следствия 1 в непрерывном виде находим:
 2) Использовав второе равенство из Следствия 1 получаем:
2) Использовав второе равенство из Следствия 1 получаем:
 .
.
Замечание 2:


Полученные с помощью этой формулы множества полиномов называются полиномами Чебышева. В отдельных случаях: 
В теории приближения функции хорошо известен следующий факт: если в качестве узлов интерполяции взять корни полинома  , то
, то  (
( )
)

В этом случае из Следствия 1 следует, что
 . Если свободная интерполяция находится в отрезке [a,b], то с помощью замены
. Если свободная интерполяция находится в отрезке [a,b], то с помощью замены 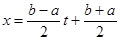 этот отрезок можно заменить на [-1;1]. В это время точки
этот отрезок можно заменить на [-1;1]. В это время точки
(11)  (
( ,
,  )
)
будут однородными с корнями  , а остаточный член записывается следующим образом:
, а остаточный член записывается следующим образом:
 .
.
Последнее неравенство полностью дает оптимальную оценку на отрезке [a,b], т.е. мы оцениваем погрешность интерполяции на отрезке [a,b], чтобы узлы (11) были оптимальными.



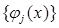 являются степенями {1, х, х2, …, хn}, то говорят об алгебраической интерполяции, а функцию
являются степенями {1, х, х2, …, хn}, то говорят об алгебраической интерполяции, а функцию  называют интерполяционным полиномом и обозначим как:
называют интерполяционным полиномом и обозначим как: (4)
(4)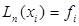 (
( ) (5),
) (5),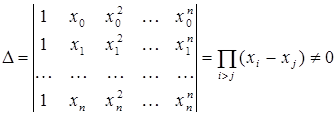 .
. ).
). ).
). ,
,

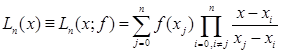



 .
. .
. (
( ). Но, в общем, это не так и
). Но, в общем, это не так и  (
( ,
,  (
(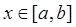 )
) разность этого выражения нужно найти.
разность этого выражения нужно найти.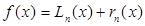 (
( )
) называют остаточным членом (или погрешность интерполяции).
называют остаточным членом (или погрешность интерполяции). [a,b] [2]
[a,b] [2] (
( ,
,  ), где
), где 
 [a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций.
[a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций. [a,b];
[a,b];
 ), рассмотрим вспомогательную функцию:
), рассмотрим вспомогательную функцию: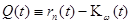 , (
, ( ).
).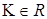 - свободный параметр, который открыто объясняет
- свободный параметр, который открыто объясняет  (
( берем проходящим через равенство
берем проходящим через равенство 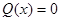 . В это время концы
. В это время концы  , будучи точками промежутка, можно использовать теорему Ролля.
, будучи точками промежутка, можно использовать теорему Ролля. :
:  (
( )
) :
: :
:  (
( :
: 
 .
. (
( ); над ними:
); над ними:  .
.
 построить полином
построить полином 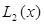 для этой функции, при:
для этой функции, при: . Оценить погрешность полинома;
. Оценить погрешность полинома;



 2) Использовав второе равенство из Следствия 1 получаем:
2) Использовав второе равенство из Следствия 1 получаем: .
.


 , то
, то  (
( )
)
 . Если свободная интерполяция находится в отрезке [a,b], то с помощью замены
. Если свободная интерполяция находится в отрезке [a,b], то с помощью замены 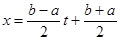 этот отрезок можно заменить на [-1;1]. В это время точки
этот отрезок можно заменить на [-1;1]. В это время точки (
( ,
,  )
) .
.


