Тема: «исследование способов формирования нечетких множеств и операций над ними».

Лабораторная работа № 1

Пример П5. Программа использования сигмоидных функций

х = 0: 0.1: 10

subplot (1, 3, 1);

y=sigmf (x, [2 4]);

plot (х, у);

xlabel ('sigmf, P = [2 4]')

subplot (1, 3, 2);

у = dsigmf (x, [5 2 5 7]);

plot (х, у);

xlabel ('dsigmf, Р = [5 2 5 7]')

subplot (1, 3, 3);

у = psigmf (x, [2 3 -5 8]);

plot (х, у);

xlabel ('psigmf, P= [2 3 -5 8]');

 

Рисунок 5 – Сигмоилные функции принадлежности

а – основная односторонняя; б – дополнительная двухсторонняя;

в — дополнительная несимметричная.

 

Инструментарий нечеткой логики (fuzzy logic toolbox) в составе Matlab предоставляет возможность формирования ФП на основе полиномиальных кривых. Соответствующие функции называются Z-функции (zmf), РI-функции (pimf) и S-функции (smf). Функция zmf представляет собой асимметричную полиномиальную кривую, открытую слева (рис. П5, а), функция smf – зеркальное отображение функции zmf (рис. П5, в). Соответственно функция pimf равна нулю в правом и левом пределах и принимает значение, равное единице, в середине некоторого отрезка.

Описание функции: у = zmf (x, [a b]).

Параметры а и b определяют экстремальные значения кривой.

Описание функции: у = pimf (x, [a b с d]).

Параметры а и d задают переход функции в нулевое значение, а параметры b и с – в единичное (рис. П5, б).

Описание функции: у = smf (х, [а b]).

Параметры а и b определяют экстремальные значения кривой.

 

Пример П6. Программа использования полиномиальных кривых

х = 0: 0.1: 10;

subplot (1, 3, 1);

у = zmf (x, [3 7]);

plot (х, у);

xlabel ('zmf, P = [3 7]');

subplot (1, 3, 2);

у = pimf (x, [1 4 5 10]);

plot (x, у);

xlabel ('pimf, P = [1 4 5 10]');

subplot (1, 3, 3);

у = smf (x, [1 8]);

plot (x, y);

xlabel ('smf, P = [1 8]').

 

(а)                   (б)                   (в)

Рисунок 6 – Полиномиальные функции принадлежности:

а – Z-функция; б – PI-функция; в – S-функция

 

Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в Mat l ab имеется возможность формировать собственные ФП или модифицировать встроенные.

 

Операции над нечеткими множествами. В операции над нечеткими множествами выделяют три основные логические операции над нечеткими множествами: конъюнкция, дизъюнкция и логическое отрицание. В среде Matlab существует возможность определять конъюнктивные и дизъюнктивные операторы с точки зрения минимаксной и вероятностной интерпретаций.

Рассмотрим минимаксную интерпретацию логических операторов, в которой конъюнктивный оператор представляет нахождение минимума – min (рис. П6, а), а дизъюнктивный – максимум – max (рис. П6, б).

Описание конъюнктивной функции: у = min ([у₁; у₂]).

Описание дизъюнктивной функции: у = mах ([у₁; у₂]).

Параметры у₁ и у₂ представляют собой исходные ФП. Функция min работает со списком ФП. В Matlab список оформляется квадратными скобками, а элементы списка разделяются точкой с запятой.

 

Пример П7. Программа использования операций min и max

x = 0: 0.1: 10;

subplot (1, 2, 1);

y1 = gaussmf (x, [3 5]);

у2 = gaussmf (x, [3 7]);

у3= min ([y1; y2]);

plot (x, [y1; у2],':');

hold on;

plot (x, у3);

hold off;

subplot (1, 2, 2);

у4 = max ([y1; у2]);

plot (x, [y1; у2], ':');

hold on;

plot (x, y4);

hold off.

 

 

(а)                                  (б)

Рисунок 7 – Пересечение (а) и объединение (б) нечетких множеств

(минимаксная интерпретация)

 

Пунктирной линией на графиках изображены исходные ФП, а сплошной линией – результат действия логических операторов.

Минимаксная интерпретация является наиболее распространенной при построении нечетких систем. Тем не менее, на практике довольно часто используется альтернативная вероятностная интерпретация конъюнктивных и дизъюнктивных операторов. Matlab содержит соответствующие функции.

В рамках данной интерпретации конъюнктивный оператор представляет собой оператор вычисления алгебраического произведения – prod (рис. П7, а), а дизъюнктивный оператор – оператор вычисления алгебраической суммы – рrоbоr (рис. П7, б).

Описание функции: у = prod ([y1; у2]).

Описание функции: у = probor ([y1; у2]).

Параметры y₁и у₂ представляют собой исходные ФП.

 

Пример П8. Программа использования вероятностных операторов конъюнкции и дизъюнкции.

х = 0: 0.1: 10;

subplot (1, 2, 1);

y1 = gaussmf (x, [3 5]);

y2 = gaussmf (x, [3, 7]);

у3 = prod ([y1; y2]);

plot (x, [y1; у2],':');

hold on;

plot (x, y3);

hold off;

subplot (1, 2, 2);

y4 = probor ([y1; y2]);

plot (x, [y1; y2], ':');

hold on;

plot (x, y4);

hold off.

 

(а)                                  (б)

Рисунок 8 – Пересечение (a) и объединение (б) нечетких множеств

(вероятностная интерпретация)

 

Дополнение нечеткого множества есть не что иное, как математическое представление вербального выражения «НЕ А»(рис. П8), где А – нечеткое множество, описывающее некоторое размытое суждение.

Описание функции дополнения: y = 1 – y*, где у* – исходная ФП.

 

Пример П9. Программа использования операции дополнения

х = 0: 0.1: 10;

y1 = gaussmf (x, [3 5]);

у = 1 - y1;

plot (х, y1, ':');

hold on;

plot (x, y);

hold off.

 

Рисунок 9 – Дополнение нечеткого множества.

Вывод: В данной практической работе изучили методы построения нечетких множеств с использованием различных типов функций принадлежности. Ознакомиться с наиболее распростра­ненными логическими операциями над нечеткими множе­ствами.

 

Лабораторная работа № 2

Теоретическая часть

Знакомство с методологией нечеткого моделирования. Описание предметной области может быть проведено посредством лингвистических переменных и правил естественного языка, содержащих качественную оценку ситуации. Основой для описания ситуации является нечеткое высказывание следующего вида:

xi есть Xi или xi = Xi,

где xi – некоторая величина, Xi – элемент терм-множества лингвистической переменной из исследуемой предметной области.

Нечеткая система выполняет отображение из входного пространства m A Ì Â в выходное пространство r B Ì Â. Такая система является системой типа «много_входов – много_выходов» (MIMO – multiple_input-multiple_output). Если система имеет m входов и r выходов и входное и выходное пространства являются многомерными, то входное пространство определяется как A = A ´ … ´ A_m, а выходное пространство – как B = B ´ … ´ B_r, где A_i,B_j Ì Â. Обозначим a = [a₁ a₂ … a_m]­^T и b = [b₁ b₂ … b_m]­^T как входной и выходной векторы, соответственно. Отображение вход/выход может быть представлено как множество нечетких правил типа «ЕСЛИ-ТО». Каждое правило состоит из двух частей: условной и заключительной. Антецедент или условная часть (ЕСЛИ-часть) содержит утверждение относительно значений входных переменных, в консеквенте или заключительной части (ТО-части) указываются значения, которые принимают выходные переменные. Таким образом, нечеткая система типа «много_входов – много_выходов» может быть задана нечеткими правилами следующего вида:

Правило 1: ЕСЛИ a₁ = A₁₁ И a₂ = A₂₁ … a_m = A_m1 ТО b₁ = B₁₁ И b₂ = B₂₁ И … И b_r = B_r1;

Правило 2: ЕСЛИ a₁ = A₁₂ И a₂ = A₂₂ … a_m = A_m2 ТО b₁ = B₁₂ И b₂ = B₂₂ И … И b_r = B_r2;

 ……….………………………………………………………………………

Правило n: ЕСЛИ a₁ = A_1n И a₂ = A_2n … a_m = A_mn ТО b₁ = B_1n И b₂ = B_2n И … И b_r = B_rn;

где a₁, a₂, …, a_m – входные переменные, b₁, b₂, …, b_r – выходные переменные, A_it и B_js – нечеткие области определения входных и выходных переменных, которые определены на универсальных множествах X₁, X₂,…, X_m, Y₁, Y₂, …, Y_r, соответственно. Каждая нечеткая область A_it связана с функцией принадлежности m_Ait(a_i).

Вход A нечеткой системы активизирует каждое из правил, хранимых в нечеткой ассоциативной памяти. Чем больше вход A соответствует антецеденту i-го правила, тем больше выход соответствует консеквенту этого правила.

Весьма популярными в практическом применении в настоящее время являются нечеткие системы типа «много_входов – один_выход». Система такого типа выполняет отображение из входного пространства A Ì Â^m в выходное пространство B Ì Â. Известно два основных типа нечетких систем «много_входов –один_выход».

Системы типа Мамдани имеют правила:

Правило i: ЕСЛИ a₁ = A_1i И a₂ = A_2i … И a_m = A_mi ТО b_i = B_i;

Другой тип – системы типа Сугено с правилами следующего вида:

Правило i: ЕСЛИ a₁ = A_1i И a₂ = A_2i … a_m = A_mi ТО b_i = f_i(a₁,… a_m); где f_i – функция, определенная на переменных a₁ … a_m.

Для описания отображения входного вектора a в значение b используются методы нечеткой логики, например, аппроксимация Мамдани или метод, основанный на формальном логическое доказательстве. В процессе вывода участвуют операции конъюнкции и дизъюнкции. Задание этих операций на основе триангулярных норм позволяет более гибко настраивать нечеткую систему на исследуемую предметную область.

В общем случае процесс создания нечетких систем состоит из следующих шагов:

1) определение входных и выходных переменных системы;

2) задание функций принадлежности каждой переменной;

3) определение нечетких правил;

4) настройка параметров функций принадлежности и нечетких правил.

При разработке базы правил необходимо руководствоваться следующими принципами:

1) в базе правил существует правило для всяких сочетаний A_1i, A_2i, …, A_mi, B_i;

2) нет двух и более правил с одинаковым антецедентом и различным консеквентом.

Для осуществления вывода в такой системе можно воспользоваться композиционным правилом. Однако предварительно нужно выполнить операции конъюнкции (И) и далее операцию объединения (агрегации) n правил.

Пусть на вход системы поступают четкие значений x₁, x₂. Требуется определить четкий выход y. Для этого необходимо выполнить следующие операции:

1) фаззификация – для каждого правила вычисляется значения  m_A1i(x₁) и m_A2i(x₂);

2) конъюнкция – объединение посылок в антецеденте каждого правила, используя t-нормальную функцию, получим T(m_A1i(x₁), m_A2i(x₂));

3) импликация – I(T(m_A1i(x₁), m_A2i(x₂)), m_Bi(y));

4) агрегация – получение нечеткого выходного значения из множества объединенных правил, то есть определение итоговой функции принадлежности m_Bi(y).

5) дефаззификация - преобразование итоговой функции принадлежности m_Bi(y) в четкое значение y.

Структура нечеткой системы моделирования представлена на рисунке 1.

Рисунок 1 – Структура нечеткой системы моделирования

Пример: Описание заданной нелинейной функции множеством правил вида ЕСЛИ-ТО.

Пусть дана функция F(x) = sin(x) и следующие области изменения 0<x<y (Рисунок 2).

Рисунок 2 – Пример нелинейной функции

Лингвистические переменные, описывающие x и F, определены на следующем множестве термов: {очень малая, малая, средняя, большая, очень большая}. Функции принадлежности для указанных термов приведены на рисунках 3 и 4. Тогда нечеткая система моделирования указанной нелинейной функции будет задана следующей базой правил:

ЕСЛИ x = очень малая ТО F = средняя,

ЕСЛИ x = малая ТО F = очень большая,

ЕСЛИ x = средняя ТО F = средняя,

ЕСЛИ x = большая ТО F = очень малая,

ЕСЛИ x = очень большая ТО F = средняя.

Рисунок 3 – Пример функций принадлежности для переменной x

Рисунок 4 – Пример функций принадлежности для переменной F

 

Практическая часть

Задание:

1. Используя пакет Matlab, построить график выбранной нелинейной функции.

2. Выбранную нелинейную функцию описать базой правил для лингвистических переменных, описывающих x и F, определенных на множестве из пяти и девяти термов.

Вариант 4 – функция z=x²-y²; Область изменения x=-4<x<4; y=-4<y<4; z=-4<z<4. Так как в области изменения была найдена не точность, z была изменена на z=-16<z<16.

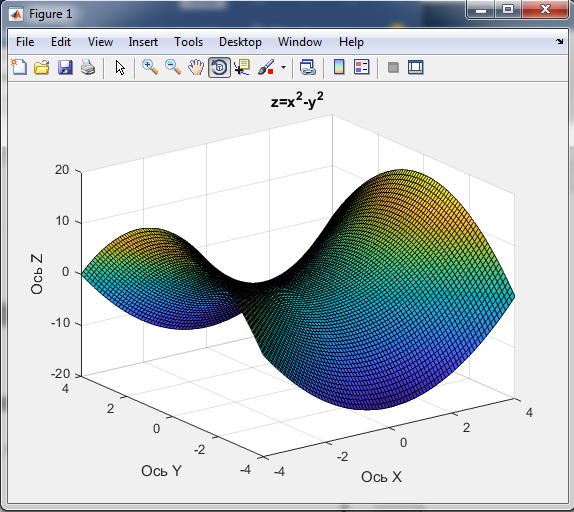
Рисунок 5

График функции построен с помощью MathLab:

%Построение графика функции z=x^2-y^2

[X,Y]=meshgrid(-4:0.1:4);

Z=X.^2.-Y.^2;

surf(X,Y,Z);

xlabel("Ось X");

ylabel("Ocь Y");

zlabel("Ось Z");

title("z=x^2-y^2");

Рисунок 6 – Модель Мамдани в Mathlab для функции z = x²-y²

 

 

 

Рисунок 7 – Параметры нечетких множеств для входа Х для 7 термов

 

 

Рисунок 8 – Параметры нечетких множеств для входа Y для 7 термов

 

 

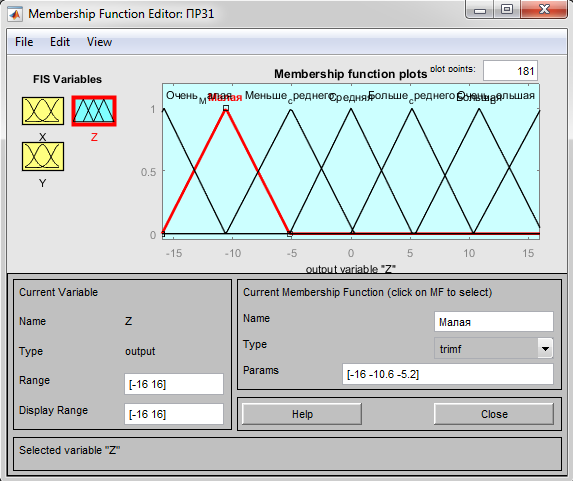
Рисунок 9 - Параметры дефазификации модели для 7 термов

 

 

Рисунок 9 – Правила вывода разрабатываемой модели

 

Рисунок 10 – Результат построения модели

 

Вывод:   В данной практической работе были изучены методологии нечеткого моделирования. Описание заданной нелинейной функции множеством правил вида ЕСЛИ-ТО по типу вывода Мамдани.

Практическая работа №4

Теоретическая часть

Система нечёткого вывода, созданные тем или иным образом с помощью пакета Fuzzy Logic Toolbox, допускают интеграцию с инструментами пакета Simulink, что позволяет выполнять моделирование систем в рамках последнего. Рассмотрим это на примере контроля уровня воды в баке.

Пример 1. Контроль уровня воды в баке.

На рисунке 1 изображен объект управления в виде бака с водой, к которому подходят две трубы: через одну трубу, снабженную краном, вода втекает в бак, через другую вытекает. Подачу воды в бак можно регулировать, больше или меньше открывая кран. Расход воды является неконтролируемым и зависит от диаметра выходной трубы (он фиксирован) и от текущего уровня воды в баке. Если понимать под выходной (регулируемой) переменной уровень воды, а под регулирующим элементом кран, то можно отметить, что подобный объект регулирования, с точки зрения его математического описания, является динамическим и существенно нелинейным.

Определим цель управления здесь как установление уровня воды в баке на требуемом (изменяющемся) уровне и попробуем решить соответствующую задачу управления средствами нечеткой логики. Очевидно, в регулятор, обеспечивающий достижение цели управления, должна поступать информация о несоответствии (разности) требуемого и фактического уровней воды, при этом данный регулятор должен вырабатывать управляющий сигнал на регулирующий элемент (кран).

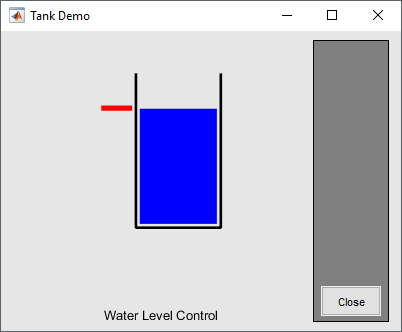
Рисунок 1 – Схематическое представление объекта управления
(бака с водой)

В первом приближении функционирование регулятора можно описать набором из следующих правил:

1. If (level is okay) then (valve is no_change) (1)

2. If (level is low) then (valve is open_fast) (1)

3. If (level is high) then (valve is closefast) (1)

 4. If (level is okay) and (rate is positive) then (valve is close_slow) (1)

5. If (level is okay and (rate is negative) then (valve is openslow) (1),

что в переводе означает:

1. Если (уровень соответствует заданному), то (кран без изменения) (1)

2. Если (уровень низкий), то (кран быстро открыть) (1) 3. Если (уровень высокий), то (кран быстро закрыть) (1)

4. Если (уровень соответствует заданному) и (его прирост положительный), то (кран надо медленно закрывать) (1)

5. Если (уровень соответствует заданному) и (его прирост отрицательный), то (кран надо медленно открывать) (1)

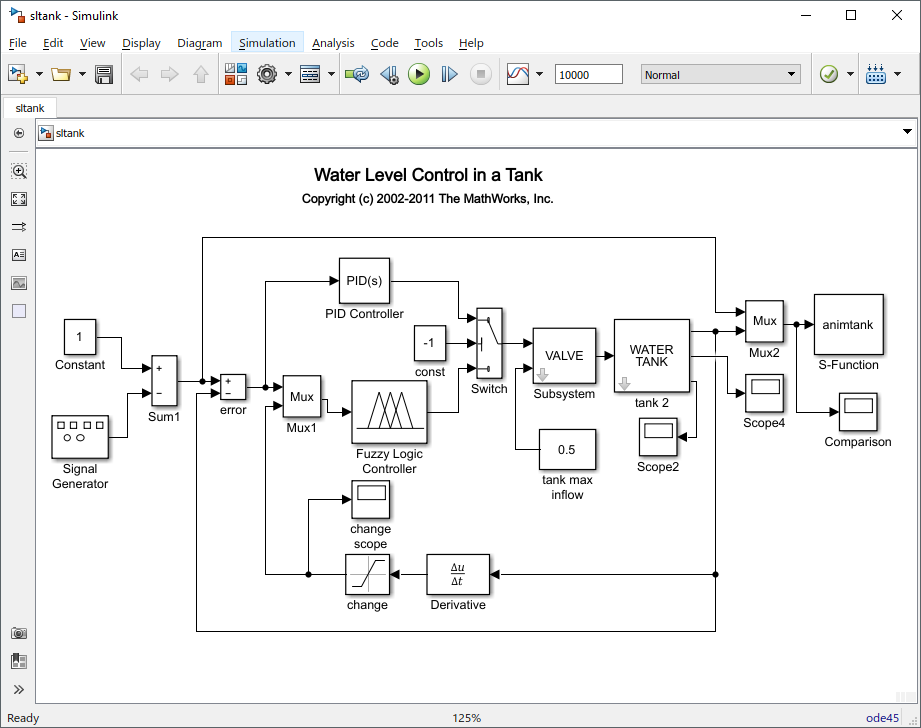
Рисунок 2 – Блок-диаграмма модели системы управления уровнем воды в баке нечётким регулятором

 Ее можно вызвать из командной строки командой sltank, что приведет к открытию окна Simulink с блок-диаграммой указанной модели (Рисунок 2). Одновременно блок Fuzzy Logic Controller будет сопоставлен с системой нечеткого вывода, записанной в файле tank.fis. Для изучения процесса функционирования системы необходимо нажать кнопку Start панели инструментов блок-диаграммы модели и дважды щелкнуть левой кнопкой мыши по блоку Comparison (Сравнение). В появившемся окне этого блока будут показаны изменяющиеся во времени сигналы заданного (последовательность импульсов прямоугольной формы) и фактического уровней воды (Рисунок 3). Как видно, переходный процесс в системе имеет апериодическую форму и заканчивается достаточно быстро, т. е. качество регулирования следует признать хорошим.

Построение нечеткой модели с использованием блоков Simulink.

Для построения какой-то собственной моделирующей системы с использованием средств нечеткой логики и блоков Simulink рекомендуется просто скопировать блок Fuzzy Logic Controller из рассмотренной системы sltank (или какого-либо другого демонстрационного примера MATLAB) и поместить его в блок-диаграмму разрабатываемой системы.

Отметим, что функционирование указанных блоков осуществляется с использованием системной S-функции sffis.mex.

Запись этой функции такова: output = sffis(t,x,u,nag,nsmat), где output – выход нечеткого регулятора, t, х и flag – стандартные аргументы системной функции Simulink, fismat – идентификатор (имя) нечеткой системы вывода, и входной сигнал (вектор входных сигналов) регулятора.

По смыслу данная функция аналогична рассмотренной выше функции evalfis, но она оптимизирована для работы в среде Simulink.

Рисунок 3 – Результаты моделирования системы управления с нечётким регулятором

Практическая часть

Задание: Опишите набором из правил функционирование регулятора, представленного в соответствующем демонстрационном примере, представьте результат моделирования.

Вариант 4: slcp – демонстрация нечеткой системы управления перевернутым маятником.

                                

Рисунок 4 –Демонстрация модели нечеткой системы управления перевернутым маятником в Simulink

Рисунок 5 – Схематичное представление задачи «нечеткой системы управления перевернутым маятником»

Рисунок 6 – Анализ переходного процесса модели slcp

Модель slcp описана правилами нечеткого вывода по Мамдани и содер-жит:

— Четыре входа:

1. in1[-0.3000 0.3000]={{in1mf1, gbellmf(0.3000 2 -0.3000 0)}, {in1mf2, gbellmf(0.3000 2 0.3000 0) }};

2. in2 [-1 1]={{in2mf1, gbellmf(1 2 -1 0)}, {in2mf2, gbellmf(1 2 1 0) }};

3. in3 [-3 3]={{in3mf1, gbellmf(3 2, 3 0)}, {in3mf2, gbellmf(3 2 3 0) }};

4. in4 [-3 3]={{in4mf1, gbellmf(3 2 -3 0)}, {in4mf2, gbellmf(3 2 3 0) }};

— Один выход: out [-10, 10] = {

— {outmf1, linear(41.3729 10.0298 3.1623 4.2875 0.3386)},

— {outmf2, linear(40.4085 10.0534 3.1623 4.2875 0.2068)},

— {outmf3, linear(41.3729 10.0298 3.1623 4.2875 0.3386)},

— {outmf4, linear(40.4085 10.0534 3.1623 4.2875 0.2068)},

— {outmf5, linear(38.5609 10.1774 3.1623 4.2875 -0.0489)},

— {outmf6, linear(37.5965 10.1537 3.1623 4.2875 -0.1807)},

— {outmf7, linear(38.5609 10.1774 3.1623 4.2875 -0.0489)},

— {outmf8, linear(37.5965 10.1537 3.1623 4.2875 -0.1807)},

— {outmf9, linear(37.5964 10.1537 3.1623 4.2875 0.1807)},

— {outmf10, linear(38.5608 10.1773 3.1623 4.2875 0.0489)},

— {outmf11, linear(37.5964 10.1537 3.1623 4.2875 0.1807)},

— {outmf12, linear(38.5608 10.1773 3.1623 4.2875 0.0489)},

— {outmf13, linear(40.4083 10.0534 3.1623 4.2875 -0.2068)},

— {outmf14, linear(41.3728 10.0297 3.1623 4.2875 -0.3386)},

— {outmf15, linear(40.4083 10.0534 3.1623 4.2875 -0.2068)},

— {outmf16, linear(41.3728 10.0297 3.1623 4.2875 -0.3386)}};

Правила нечеткого вывода по Мамдани описывающие модель slbb:

1. in1==in1mf1 & in2==in2mf1 & in3==in3mf1 & in4==in4mf1 => out=outmf1 (1)

2. in1==in1mf1 & in2==in2mf1 & in3==in3mf1 & in4==in4mf2 => out=outmf2 (1)

3. in1==in1mf1 & in2==in2mf1 & in3==in3mf2 & in4==in4mf1 => out=outmf3 (1)

4. in1==in1mf1 & in2==in2mf1 & in3==in3mf2 & in4==in4mf2 => out=outmf4 (1)

5. in1==in1mf1 & in2==in2mf2 & in3==in3mf1 & in4==in4mf1 => out=outmf5 (1)

6. in1==in1mf1 & in2==in2mf2 & in3==in3mf1 & in4==in4mf2 => out=outmf6 (1)

7. in1==in1mf1 & in2==in2mf2 & in3==in3mf2 & in4==in4mf1 => out=outmf7 (1)

8. in1==in1mf1 & in2==in2mf2 & in3==in3mf2 & in4==in4mf2 => out=outmf8 (1)

9. in1==in1mf2 & in2==in2mf1 & in3==in3mf1 & in4==in4mf1 => out=outmf9 (1)

10. in1==in1mf2 & in2==in2mf1 & in3==in3mf1 & in4==in4mf2 => out=outmf10 (1)

11. in1==in1mf2 & in2==in2mf1 & in3==in3mf2 & in4==in4mf1 => out=outmf11 (1)

12. in1==in1mf2 & in2==in2mf1 & in3==in3mf2 & in4==in4mf2 => out=outmf12 (1)

13. in1==in1mf2 & in2==in2mf2 & in3==in3mf1 & in4==in4mf1 => out=outmf13 (1)

14. in1==in1mf2 & in2==in2mf2 & in3==in3mf1 & in4==in4mf2 => out=outmf14 (1)

15. in1==in1mf2 & in2==in2mf2 & in3==in3mf2 & in4==in4mf1 => out=outmf15 (1)

16. in1==in1mf2 & in2==in2mf2 & in3==in3mf2 & in4==in4mf2 => out=outmf16 (1)

 

Вывод: были приобретены навыки работы Fuzzy Logic с блоками Simulink.

 

Практическая работа №5

 Тема: «ИЗУЧЕНИЕ СВОЙСТВ ЛИНЕЙНОГО НЕЙРОНА И ЛИНЕЙНОЙ НЕЙРОННОЙ СЕТИ»

Цель работы: изучить свойства линейного нейрона.

 

Теоретическая часть

Искусственные нейронные сети (НС) представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов). Очень грубо структуру биологического нейрона можно описать следующим образом. Нейрон имеет сому – тело, дерево входов – дендриты, выход – аксон. На соме и на дендритах распола­гаются окончания аксонов других нейронов, называемых си­напсами. Принятые синапсами входные сигналы стремятся либо возбудить нейрон, либо затормозить. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. В соответствии с приведенным описа­нием математическая модель нейрона представляет собой суммирующий пороговый элемент (рис. 1).

 

 

Рис. 1. Искусственный нейрон

 

 

Формула срабатывания нейрона:

 

 

Описание основных функций

Для работы с нейронными сетями необходимо инсталли­ровать MATLAB и обладать первоначальными знаниями относи­тельно языка системы. Поскольку MATLAB представляет собой интерпретатор, то обучение инструментарию нейронных сетей заключается в основном в изучении функций и их параметров. Узнать возможности нейрона как классификатора простых линейно сепарабельных задач можно путем проведения экс­периментов с моделью одного линейного нейрона.

Функция newp. Для того чтобы создать нейрон, используют функцию newp, имеющую следующий синтаксис:

где PR – матрица минимальных и максимальных R входных эле­ментов; S – количество нейронов (при создании одного нейрона S =1); TF – функция активации (transfer function); LF – имя функции обучения нейрона.

В случае если параметры функции newp не заданы, их зна­чения определяются посредством ввода значений в диалого­вые окна. Построенный нейрон характеризуется функциями весов (weight function), входов сети (net input function) и оп­ределенной функцией активации. Функция весов – это ум­ножение весов на входной сигнал, функция входов сети – их сумма. Веса задаются как для входов нейрона, так и для фик­сированного входа, задающего порог срабатывания (bias). Вектор весов инициализируется нулями. Для обучения ис­пользуются функции, рассмотренные ниже.

Функция learnp настраивает веса нейрона. Синтаксис функции обучения довольно сложен:

 

 

Функция lea rn p (W, P, Z, N, A, T, E, gW, gA, D, LP, LS) имеет несколько входов, где вектор W – вектор весов; Р – вектор входов; Z – вектор взвешенных входов; N – вектор сети; А – вектор выхода; Т – вектор желаемых выходов; Е – вектор ошибок; gW – вектор изменения весов; gA – изменения вы­ходов. Функция возвращает значения: dW – изменения мат­рицы весов; LS – новый уровень обученности.

Функция learnp может быть использована с параметрами по умолчанию:

 

 

Использование пустого списка [ ] означает параметр по умолчанию.

Функция learnp вычисляет изменение весов dW для задан­ного нейрона в соответствии с правилом обучения персептрона:

 

 

т. е. .

Функция learnpn настраивает нормализованные веса:

 

 

Функция learnpn вычисляет изменение весов dW для дан­ного нейрона и его входа Р и ошибки Е в соответствии с нор­мализованным правилом обучения персептрона:

 

 

т. е. .

 

Линейный нейрон имеет одно существенное ограничение. Входные векторы должны быть линейно разделимы. Если векторы невозможно отделить прямой или гиперплоскостью, то персептрон не способен решить задачу классификации.

Функция adapt адаптирует НС к условиям задачи:

 

 

Параметры функции adapt: net – имя сети; Р – входы сети; T – желаемый выход; Р _i – исходные условия задержки; A _i – ис­ходные условия задержки для слоя. Функция возвращает па­раметры адаптированной сети net.adaptParam: net – изменен­ная сеть; Y – выход сети; Е – ошибки сети; Pf – условия за­держки входов; Af – условия задержки слоя. Параметры Р _i и Pf необязательные и необходимы только для сетей, имеющих задержки на входах и слое.

Функция train также обучает НС и использует следующий синтаксис:

 

 

Функция train имеет следующие парамет­ры: net – сеть; Р – входы сети; Т – желаемый выход; Р _i – исходные условия задержки входа; A _i – исходные условия за­держки слоя.

Функция sim имитирует нейронную сеть:

 

 

где net – сеть; Р – входы сети; P _i — исходные условия задержки входов сети; A _i – исходные условия задержки слоя. Функция возвращает Y – выходы сети; Pf – окончательные условия задержки входов; Af – окончательные условия задержки слоя.

Функции активации. Ниже представлены назначения этих функций.

 

Функция	Назначение
hardlim	Возвращает 1, если на входе положительное число и 0 в противном случае.
tansig	Вычисляет гиперболический тангенс от входа.
purelin	Вычисляет выход слоя от сетевого входа.

 

Функции графического интерфейса и вспомогательные функции. Назначение этих функций представлено ниже.

 

Функция	Назначение
axis([Xmin Xmax Ymin Ymax)	Устанавливает диапазоны координатных осей.
title(‘ строка ’)	Выводит в графическое окно рисунков заголовок графика.
rand(M, N)	Возвращает матрицу размерности М на N сослу­чайными значениями.
xlabel (‘ строка ’) ylabel (‘ строка ’)	Подписывают наименование координатных осей.
cla reset	Очищает координатную сетку в окне рисунков.
hold on hold off	Включают и отключают режим добавления графи­ков на координатную сетку.
text(X, Y, ‘ строка ’)	Выводит строку, начиная с указанных координат в поле рисунков.
pause (n)	Ожидает пользовательского ответа п секунд.
plot (X, Y, ‘цвет и символ’)	Изображает на координатной сетке точки с коор­динатами, заданными векторами X, Y, с помощью указанного символа и цвета.
plotpv(P, V)	Изображает точки Р указанными маркерами Т, где Р – матрица входных векторов размерностью R на Q (R должен быть 3 или меньше), Т – матрица дво­ичных векторов размерностью 5 на Q (S должен быть 3 или меньше).
plotes (WV, BV, ES, V)	Изображает поверхность ошибки на отдельном входе, где WV – вектор строк значений весов W размерности N, BV – вектор строк значений поро­гов В размерности М, ES – матрица ошибки раз­мерности М на N, V – угол зрения по умолчанию [-37, 5, 30].
plotsom(POS)	Изображает позицию нейрона красной точкой, связывая синей линией нейроны, находящиеся друг от друга на расстоянии 1. POS – матрица S N -размерных нейронов.
ind2vec vec2ind	Позволяют представить индексы либо собственно значениями индексов, либо векторами, строки ко­торых содержат 1 в позиции индекса.
full	Преобразует разреженную матрицу в полную.
maxlinlr(P)	Функция возвращает максимальный уровень обученности линейного слоя без bias, который обучал­ся только на векторе Р.
trainlm	Выполняет обучение многослойной НС методом Левенберга-Марквардта.
netprod	Входная сетевая функция, которая вычисляет вы­ход сетевого слоя, умножая входной вектор на веса и прибавляя bias.
init	Итеративно инициализирует НС.

 

Структура данных описания нейронных сетей. Структура данных net – это описание обученной НС. Обучение осу­ществляется в соответствии со следующими параметрами, значения которых либо устанавливаются пользователем, либо по умолчанию.

 

Структура данных	Комментарий
net.trainParam. epochs 100	Максимальное количество эпох обучения.
net. trainParam.goal 0	Целевое значение ошибки.
net.trainParam.max_fail 5	Максимальное значение ошибки.
net.trainParam.mem reduc 1	Фактор оптимизации процесса обучения: оптимизация использования памяти или времени процессора.
net. trainParam. min_grad 1e-10	Минимальное значение градиента.
net.trainParam.show 25	Количество эпох между показами.
net.trainParam.time inf	Максимальное время обучения в секундах.
TR	Структура данных, содержащая значения об обученности НС в текущую эпоху.
TR. epoch	Номер эпохи.
TR.perf	Уровень обученности (Trainingperformance).
TR.vperf	Степень качества (Validation performance).
TR.tperf	Результативность обработки теста (Testper ­ formance).
TR.mu	Значение адаптивности.

 

Структура данных описания адаптированной НС net. adaptfcn включает в себя следующие поля net. adapt. param: NET – адаптированная НС; Y – выходы НС; Е – ошибки НС; Pf – окончательные входные значения задержек; Af – окончательные выходные задержки; TR – результат обучения (эпохи и целевая ошибка). Проведем в среде Matlab toolbox эксперименты, используя рассмотренные функции.

Ход работы

Создание нейронов, реализующих функ­ции логического И и логического ИЛИ

Создадим нейрон с одним двухэлементным входом (интервалы первого и второго элементов [0; 1]). Определим два первых параметра функции newp, а в качестве значений третьего и четвертого параметра (типа функции активации и имени процедуры обучения) воспользуемся значениями по умолчанию.

Код нейрона выполняющего функцию логического И:

>> net = newp([0 1; -2 2], 1);

>> % создание последовательности значений входа

P1 = {[0; 0] [0; 1] [1; 0] [1; 1]};

% имитация работы нейрона net на последовательности входов Р

% желаемых выходов – Т1, которая позволит нам провести адаптацию

% нейрона (обучить его) через 20 проходов.

Y = sim (net, P1);

% создание последовательности выходов

T1 = {0, 0, 0, 1};

% установка количества проходов (циклов) адаптации

net.trainParam.passes = 20;

% адаптация нейрона net для обучающей выборки <Р1; Т1>

net = train (net, P1, T1);

% симуляция работы нейрона net на последовательности входов P1

Y = sim (net, P1);

 

Рисунок 1 – Результат обучения сети

 

Для переобучения нейрона на выполнение функции ИЛИ переопределим входы Р и выходы Т.

 

Код для логического ИЛИ:

% создание последовательности входов

P2 = [0 0 1 1; 0 1 0 1];

% создание последовательности выходов (реакций) для нейрона,

% выполняющего функцию логического ИЛИ

T2 = [0, 1, 1, 1];

% Инициализируем нейрон, обучим его на 20 проходах (эпохах)

% инициализация нейрона net

net = init (net);

% имитация работы нейрона net на последовательности входов Р2

Y = sim (net, P2);

% установка количества проходов

net.trainParam.epochs = 20;

% обучение нейрона net на обучающей выборке <Р2, Т2>

net = train(net, P2, T2);

% имитация работы нейрона net на последовательности входов Р2

Y = sim (net, P2);

 

Рисунок 2 – Результат обучения сети

 

Обучение нейрона классификации векто­ров на две категории

Начнем с классификации векторов на основе двухвходового нейрона. Будем использовать функцию newp для создания нейрона, sim для имитации его работы, adapt для адаптации (обучения) нейронной сети. Обучим двухвходовый нейрон классифицировать входные векторы на две категории.

Код:

>> % определение четырех двухэлементных входов

P = [ -0.5 -0.5 0.4 -0.2; -0.5 0.5 -0.4 1.0];

% зададим желаемые выходы нейрона для определенных векторов

T = [1 1 0 0];

% изобразим входные векторы (точки) на плоскости:

plotpv(P, T);

 

Рисунок 3 - Входные векторы (точки) на плоскости

 

Создадим один линейный нейрон с двумя входами, значения которых лежат в интервале [-1, 1].

Нейрон по умолчанию имеет функцию активации hardlim и такой нейрон разделяет входные векторы прямой линией.

Определим координаты линии классификации: веса (IW) и порог срабатывания нейрона (b).

Код:

% получение управляющей структуры linehandle для изображения

% разделяющей линии в координатах весов (IW) и порога

% срабатывания нейрона (b)

linehandle = plotpc (net.IW{1}, net.b{1});

% изображение разделяющей прямой

plotpc(net.IW{1}, net.b{1});

Если исходным весам задать нулевые значения, то любые входы дадут одинаковые выходы, и линия классификации не будет видна на плоскости. Проведем обучение:

>> % очистка координатных осей

cla;

% изображение входных векторов двух категории, категория задается

% элементами вектора Т

plotpv(P, T);

% получение управляющей структуры linehanctle

linehandle = plotpc(net.IW{1}, net.b{1});

% присвоение начального значения ошибки

E = 1;

% инициализация нейрона

net = init (net);

% получение управляющей структуры linehandle

linehandle = plotpc (net.IW{1}, net.b{1});

% организация цикла пока ошибка не равна 0

while (mse(E))',

% адаптация нейрона net на обучающей выборке <Р, Т>,

% функция возвращает адаптированный нейрон net,

% выход Y, ошибку Е

[net, Y, E] = adapt (net, P, T);

% изображение разделяющей прямой нейрона после адаптации

linehandle = plotpc(net.IW{1}, net.b{1}, linehandle);

% очистка окна графиков

drawnow;

% конец цикла while

end;