А=  [1.10]- основная матрица, её элементами являются коэффициенты при неизвестных;
[1.10]- основная матрица, её элементами являются коэффициенты при неизвестных;
В=  [1.11]- матрица столбец свободных членов; Х=
[1.11]- матрица столбец свободных членов; Х= 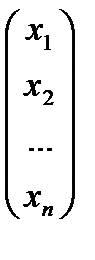 [1.12]- матрица столбец неизвестных; С=
[1.12]- матрица столбец неизвестных; С=  [1.13]- расширенная матрица.
[1.13]- расширенная матрица.
Пример
 , А=
, А= 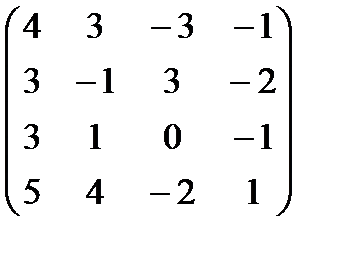 - основная матрица;
- основная матрица;
В=  - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х=  - матрица столбец неизвестных; С=
- матрица столбец неизвестных; С=  - расширенная матрица.
- расширенная матрица.
Решение систем линейных уравнений матричным методом
 , А=
, А= 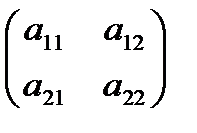 - основная матрица; В=
- основная матрица; В=  - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х= 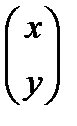 - матрица столбец неизвестных.
- матрица столбец неизвестных.
Х= А-1В [1.14]- формула для решения систем линейных уравнений матричным методом.
Пример
1) 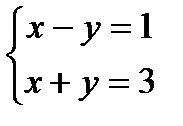 , А=
, А=  , В=
, В=  , Х=
, Х=  , А-1=
, А-1= 
 ;
;
применим формулу: Х= А-1В= 

 =
=  , значит х=2, у=1.
, значит х=2, у=1. 
2)  , А=
, А= 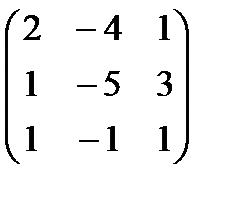 , В=
, В=  , Х=
, Х=  , А-1=-
, А-1=- 
 ;
;
применим формулу: Х= А-1В=- 

 =
=  , значит х1=2, х2=0, х3=-1.
, значит х1=2, х2=0, х3=-1.
Решение систем линейных уравнений методом Крамера
Для решения система n линейных уравнений с n неизвестными применяются формулы: х1=  , х2=
, х2=  , …, х n=
, …, х n=  [1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.
[1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.
Частные случаи
1) Пусть Д≠0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система имеет единственное решение.
2) Пусть Д=0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система не имеет решений.
3) Пусть Д=0, ДХ1=0, ДХ2=0, …, ДХn=0- тогда система имеет бесконечное множество решений (см. метод Гаусса).
Однородная система линейных уравнений
1) Пусть Д≠0, ДХ1=0, ДХ2=0, …, ДХn=0- тогда система имеет единственное решение (х1=х2=…=хn=0).
2) Пусть Д=0, ДХ1=0, ДХ1=0, …, ДХn=0- тогда система имеет бесконечное множество решений (см. метод Гаусса).
Пример
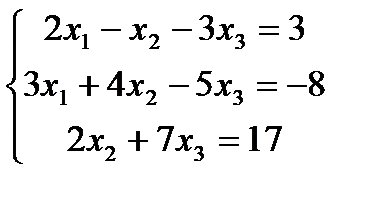 , Д=
, Д=  =79, ДХ1=
=79, ДХ1=  =395, ДХ2=
=395, ДХ2=  =-158, ДХ3=
=-158, ДХ3=  =237, х1 =
=237, х1 =  = 5, х2 =
= 5, х2 =  =- 2, х3=
=- 2, х3=  =3.
=3.
Решение систем линейных уравнений методом Гаусса
Расширенную матрицу (в данном случае система из 3 уравнений с тремя неизвестными) при помощи элементарных преобразований строк приводим к виду:  [1.16],
[1.16],
тогда х1=  , х2=
, х2= 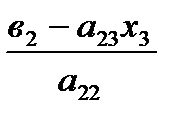 , х1=
, х1=  [1.17].
[1.17].
Пример
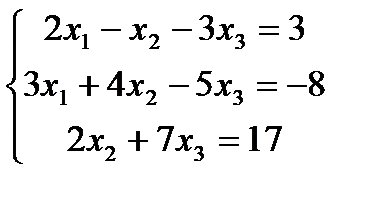 ;
;
составим расширенную матрицу; при помощи элементарных преобразований строк получим нули во втором столбике, для этого: 2стр.+1стр.  4, 3стр.+1стр
4, 3стр.+1стр  2;
2;
затем получим нули в третьем столбике, для этого: 1стр.+3стр.  3, 2стр.+3стр.
3, 2стр.+3стр.  17;
17;
преобразованную матрицу запишем при помощи системы; из системы выражаем х1, х2, х3. 
 ~
~  ~
~  =
=  , х1=5, х2=-2, х3=3.
, х1=5, х2=-2, х3=3.
Теорема Кронекера- Капелли
Пусть А- основная матрица, В- расширенная матрица, тогда, если rangА= rangВ, то система имеет решения:
1) если rangА= rangВ=n, (где n-число неизвестных), то система имеет единственное решение,
2) если rangА= rangВ<n, (где n-число неизвестных), то система имеет бесконечное множество решений;
если rangА≠ rangВ, то система не имеет решений.
Пример
Проверить системы на совместность и решить их методом Гаусса
1)  ,
,
составим расширенную матрицу; при помощи элементарных преобразований строк получим нули во втором столбике, для этого: 2стр.+1стр.  2, 3стр.+1стр;
2, 3стр.+1стр;
затем получим нули в третьем столбике, для этого: 2стр.+3стр; rangА= rangВ=n- система имеет единственное решение; преобразованную матрицу запишем при помощи системы; из системы выражаем х1, х2, х3.  ~
~  ~
~  =
=  , х1=-1, х2=-1, х3=-1.
, х1=-1, х2=-1, х3=-1.
2)  ,
,
составим расширенную матрицу; при помощи элементарных преобразований строк получим нули в третьем столбике, для этого: 2стр.+1стр. 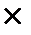 3, 3стр.+1стр
3, 3стр.+1стр 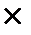 2;
2;
затем 3стр.-2стр; rangА=2, rangВ=3, rangА≠rangВ - система не имеет решений.
 ~
~  ~
~  .
.
3)  ,
,
составим расширенную матрицу; при помощи элементарных преобразований строк получим нули в третьем столбике, для этого: 2стр.+1стр.  5, 3стр.+1стр
5, 3стр.+1стр  4;
4;
затем 2стр.-3стр; rangА=rangВ=2<n (n=3) - система имеет бесконечное множество решений; преобразованную матрицу запишем при помощи системы; из системы выражаем х1, х2, х3.
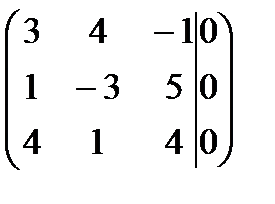 ~
~  ~
~  =
=  , х1=
, х1= 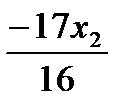 , х2, х3=
, х2, х3=  .
.



 [1.10]- основная матрица, её элементами являются коэффициенты при неизвестных;
[1.10]- основная матрица, её элементами являются коэффициенты при неизвестных; [1.11]- матрица столбец свободных членов; Х=
[1.11]- матрица столбец свободных членов; Х=  [1.12]- матрица столбец неизвестных; С=
[1.12]- матрица столбец неизвестных; С=  [1.13]- расширенная матрица.
[1.13]- расширенная матрица. , А=
, А= 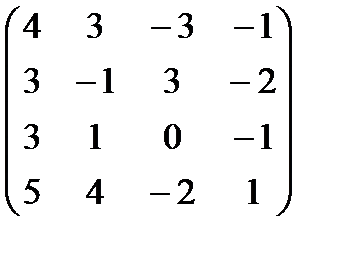 - основная матрица;
- основная матрица; - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х=  - матрица столбец неизвестных; С=
- матрица столбец неизвестных; С=  - расширенная матрица.
- расширенная матрица. , А=
, А= 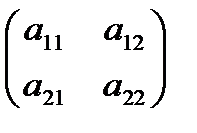 - основная матрица; В=
- основная матрица; В=  - матрица столбец свободных членов; Х=
- матрица столбец свободных членов; Х= 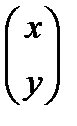 - матрица столбец неизвестных.
- матрица столбец неизвестных.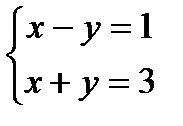 , А=
, А=  , В=
, В=  , Х=
, Х=  , А-1=
, А-1= 
 ;
; , значит х=2, у=1.
, значит х=2, у=1. 
 , А=
, А= 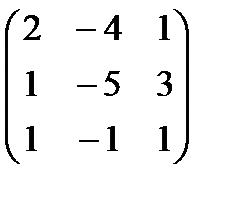 , В=
, В=  , Х=
, Х=  , А-1=-
, А-1=- 
 ;
;
 , значит х1=2, х2=0, х3=-1.
, значит х1=2, х2=0, х3=-1. , х2=
, х2=  , …, х n=
, …, х n=  [1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.
[1.15]; где х1, х2, …, хn- неизвестные, Д- определитель основной матрицы; ДХ1- определитель основной матрицы в котором первый столбец заменили столбцом свободных членов, ДХ2- определитель основной матрицы в котором второй столбец заменили столбцом свободных членов, …., ДХn- определитель основной матрицы в котором n-ый столбец заменили столбцом свободных членов.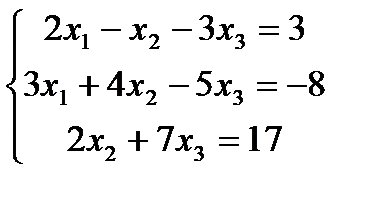 , Д=
, Д=  =79, ДХ1=
=79, ДХ1=  =395, ДХ2=
=395, ДХ2=  =-158, ДХ3=
=-158, ДХ3=  =237, х1 =
=237, х1 =  =3.
=3. [1.16],
[1.16], , х2=
, х2= 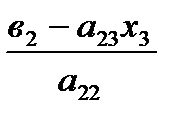 , х1=
, х1=  [1.17].
[1.17]. 4, 3стр.+1стр
4, 3стр.+1стр  2;
2; ~
~  ~
~  =
=  , х1=5, х2=-2, х3=3.
, х1=5, х2=-2, х3=3. ,
, ~
~  ~
~  =
=  , х1=-1, х2=-1, х3=-1.
, х1=-1, х2=-1, х3=-1. ,
, 3, 3стр.+1стр
3, 3стр.+1стр  ~
~  ~
~  .
. ,
,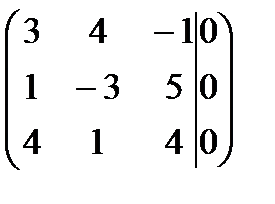 ~
~  ~
~  =
=  , х1=
, х1= 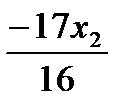 , х2, х3=
, х2, х3=  .
.

