КОНТРОЛЬНАЯ РАБОТА № 4
Теория вероятностей. Случайные события.
Случайные величины.
Методические указания и задания
Задание к разделу 2.
а) Студент знает k вопросов из n вопросов программы. Экзаменатор задает три произвольных вопроса из имеющихся. Найти вероятность того, что студент знает ответы а) на все три вопроса; б) только на два вопроса; в) только на один вопрос; г) не знает ответа ни на один из заданных вопросов.
б) Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 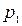 , вторым -
, вторым - 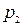 , третьим -
, третьим - 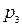 . Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.
. Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.
| №
|
|
|
|
|
|
|
|
|
|
|

| 0,9
| 0,6
| 0,7
| 0,9
| 0,7
| 0,6
| 0,5
| 0,4
| 0,5
| 0,7
|

| 0,8
| 0,7
| 0,6
| 0,5
| 0,8
| 0,4
| 0,7
| 0,7
| 0,6
| 0,4
|

| 0,7
| 0,8
| 0,5
| 0,7
| 0,7
| 0,5
| 0,8
| 0,9
| 0,9
| 0,9
|
Задание к разделу 3.
Куплено n лотерейных билетов. Вероятность выигрыша на один лотерейный билет р=0,3. Найти а) вероятность того, что из n билетов k билетов выиграют; б) наивероятнейшее число выигрышных билетов.
Задание к разделу 4.
Дискретная случайная величина может принимать только два значения: 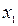 и
и 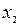 , причем
, причем 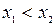 . Известны вероятность
. Известны вероятность 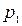 возможного значения
возможного значения 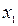 , математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
, математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
| №
|
|
|
|
|
|
|
|
|
|
|
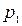
| 0,1
| 0,3
| 0,5
| 0,7
| 0,9
| 0,9
| 0,8
| 0,6
| 0,4
| 0,2
|
| М(Х)
| 3,9
| 3,7
| 3,5
| 3,3
| 3,1
| 2,2
| 3,2
| 3,4
| 3,6
| 3,8
|
| D(X)
| 0,09
| 0,21
| 0,25
| 0,21
| 0,09
| 0,36
| 0,16
| 0,24
| 0,24
| 0,16
|
Раздел 5. Непрерывные случайные величины.
В теории вероятностей и ее приложениях часто встречаются такие случайные величины, возможные значения которых сплошь заполняют некоторый интервал (a,b) конечный или бесконечный. Такие случайные величины называются непрерывными. Закон распределения вероятностей непрерывной случайной величины Х должен позволять находить вероятность попадания ее значений в любой интервал, Лежащий внутри (a,b). При этом вероятность попадания случайной величины в интервал (х,х+Dх) малой длины Dх>0 можно приближенно считать пропорциональной длине этого интервала: Р(х<X<x+Dх)» f(x)Dх, где функция 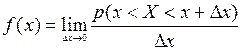 называется функцией плотности распределения вероятностей случайной величины Х, а произведение f(x)Dх = f(x)dx – элементом вероятности.
называется функцией плотности распределения вероятностей случайной величины Х, а произведение f(x)Dх = f(x)dx – элементом вероятности.
Свойства функции плотности:
1) f(x) ³, xÎ(-¥,+¥);
2) вероятность попадания случайной величины Х в интервал ( ) равна
) равна  ;
;
3) 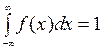 .
.
Плотность распределения вероятностей вполне определяет закон распределения непрерывной случайной величины Х.
Так как  , то функция F(x) является первообразной функции f(x): F¢(x)=f(x), откуда следует, что для непрерывной случайной величины Х функция распределения F(x) является непрерывной. Если задана функция плотности f(x), то функция распределения может быть найдена по формуле
, то функция F(x) является первообразной функции f(x): F¢(x)=f(x), откуда следует, что для непрерывной случайной величины Х функция распределения F(x) является непрерывной. Если задана функция плотности f(x), то функция распределения может быть найдена по формуле
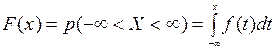 .
.
Функция F(x) называется интегральной функцией, а функция f(x) – дифференциальной.
Математическим ожиданием (средним значением, центром распределения) М(Х) непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
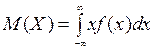
Дисперсию непрерывной случайной величины удобно вычислять по той же упрощенной формуле, что и в дискретном случае
 , где
, где  .
.
Укажем некоторые из наиболее часто встречающихся законов распределения непрерывных случайных величин.
Равномерное распределение в интервале (а,b). Говорят, что случайная величина распределена равномерно в конечном интервале (а,b), если все ее возможные значения сосредоточены на этом интервале, и плотность распределения ее вероятностей на этом интервале постоянна. Функция плотности распределения задается формулой:

Числовые характеристики:  ,
, 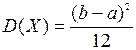 ;
; 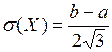 .
.
Нормальный закон распределения. Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
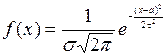 ,
,  , где
, где 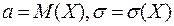 .
.
Вероятность того, что случайная величина Х примет значения из интервала 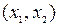 определяется с помощью интегральной функции Лапласа
определяется с помощью интегральной функции Лапласа
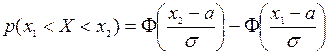 .
.
Справедливо «правило трех сигм»: R(½C-а½<3s)=,9973, которое позволяет при решении практических задач применять нормальный закон распределения к случайным величинам, заданным на конечном интервале. К нормальному распределению обычно приводят задачи, связанные с распределением сумм большого числа случайных величин.
Показательный закон распределения. Плотность вероятностей определяется формулой
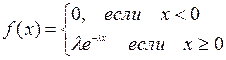 .
.
Формула распределения показательного закона
 .
.
Числовые характеристики:  .
.
К показательному закону распределения вероятностей приводит задача о распределении промежутка времени Х между двумя последовательными событиями в простейшем потоке.
Пример. Случайная величина Х задана функцией распределения

Требуется:
1) определить коэффициент А;
2) найти функцию распределения F(x);
3) схематично построить графики функций f(x) и F(x);
4) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х;
5) определить вероятность того, что Х примет значения из интервала (8; 11).
Решение. 1)Коэффициент А можно определить из условия 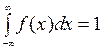 .
.
 ,
,
откуда 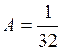 ;
; 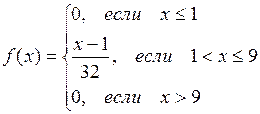 .
.
2) Функцию распределения найдем из соотношения  . Если x£1, то
. Если x£1, то 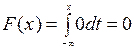 ; если 1<x£9, то
; если 1<x£9, то 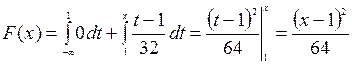 ; если х>9, то
; если х>9, то 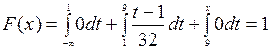 . Таким образом, функция распределения имеет вид
. Таким образом, функция распределения имеет вид 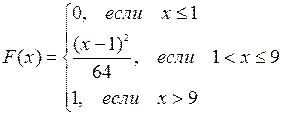 .
.
3) Графики функций f(x) и F(x) изображены на рисунках.
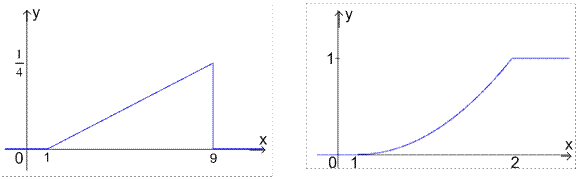
Рис 4. Функция плотности. Рис. 5. Функция распределения.
4) Найдем математическое ожидание и дисперсию случайной величины Х:  . Для вычисления дисперсии найдем
. Для вычисления дисперсии найдем 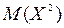 :
:  Воспользуемся формулой
Воспользуемся формулой  :
: 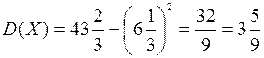 . Среднее квадратическое отклонение случайной величины Х:
. Среднее квадратическое отклонение случайной величины Х: 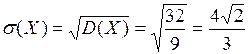 .
.
5). Вероятность того, что случайная величина попадет в некоторый интервал, можно найти или с помощью функции плотности, или с помощью функции распределения. Рассмотрим оба варианта: 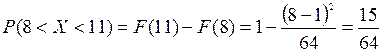 ;
; 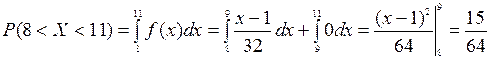 .
.
Теоретические вопросы к разделу 5.
1. Функция плотности распределения вероятностей.
2. Числовые характеристики непрерывных случайных величин.
3. Функция распределения вероятностей непрерывной случайной величины.
4. Равномерное распределение.
5. Показательный закон распределения.
6. Нормальный закон распределения.
Задание к разделу 5.
Непрерывная случайная величина Х задана своей плотностью распределения вероятностей f(x). Требуется:
1) определить коэффициент А;
2) найти функцию распределения F(x);
3) схематично построить графики функций f(x) и F(x);
1) вычислить математическое ожидание, дисперсию и среднее
квадратическое отклонение случайной величины Х;
2) определить вероятность того, что Х примет значения из интервала
(a, b).
1. 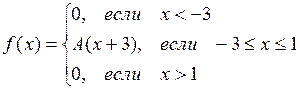 ,
,  .
.
2. 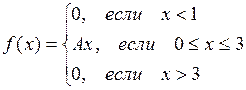 ,
,  .
.
3.  ,
,  .
.
4.  ,
,  .
.
5.  ,
,  .
.
6.  ,
, 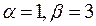 .
.
7.  ,
, 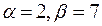 .
.
8. 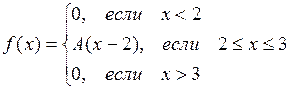 ,
,  .
.
9.  ,
, 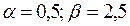 .
.
10.  ,
,  .
.
КОНТРОЛЬНАЯ РАБОТА № 4
Теория вероятностей. Случайные события.
Случайные величины.
Методические указания и задания



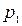 , вторым -
, вторым - 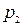 , третьим -
, третьим - 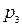 . Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.
. Найти вероятность того, что: а) только два стрелка попали в цель; б) все три стрелка попали в цель.


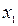 и
и 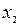 , причем
, причем 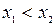 . Известны вероятность
. Известны вероятность 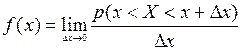 называется функцией плотности распределения вероятностей случайной величины Х, а произведение f(x)Dх = f(x)dx – элементом вероятности.
называется функцией плотности распределения вероятностей случайной величины Х, а произведение f(x)Dх = f(x)dx – элементом вероятности. ) равна
) равна  ;
;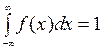 .
. , то функция F(x) является первообразной функции f(x): F¢(x)=f(x), откуда следует, что для непрерывной случайной величины Х функция распределения F(x) является непрерывной. Если задана функция плотности f(x), то функция распределения может быть найдена по формуле
, то функция F(x) является первообразной функции f(x): F¢(x)=f(x), откуда следует, что для непрерывной случайной величины Х функция распределения F(x) является непрерывной. Если задана функция плотности f(x), то функция распределения может быть найдена по формуле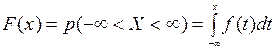 .
.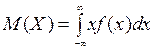
 , где
, где  .
.
 ,
, 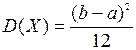 ;
; 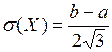 .
.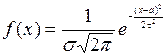 ,
,  , где
, где 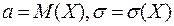 .
.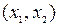 определяется с помощью интегральной функции Лапласа
определяется с помощью интегральной функции Лапласа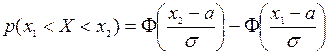 .
.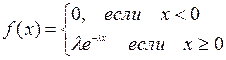 .
. .
. .
.
 ,
,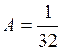 ;
; 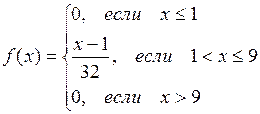 .
. . Если x£1, то
. Если x£1, то 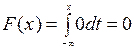 ; если 1<x£9, то
; если 1<x£9, то 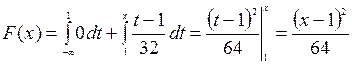 ; если х>9, то
; если х>9, то 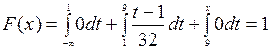 . Таким образом, функция распределения имеет вид
. Таким образом, функция распределения имеет вид 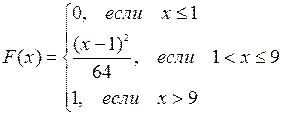 .
.
 . Для вычисления дисперсии найдем
. Для вычисления дисперсии найдем 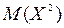 :
:  Воспользуемся формулой
Воспользуемся формулой 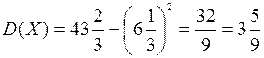 . Среднее квадратическое отклонение случайной величины Х:
. Среднее квадратическое отклонение случайной величины Х: 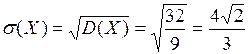 .
.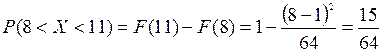 ;
; 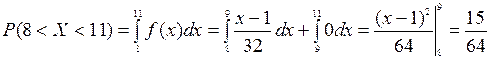 .
.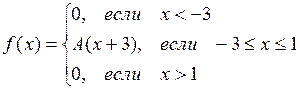 ,
,  .
.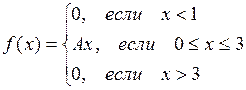 ,
,  .
. ,
,  .
. ,
,  .
. ,
,  ,
, 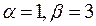 .
. ,
, 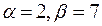 .
.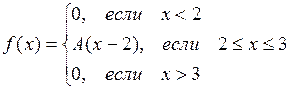 ,
,  .
. ,
, 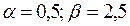 .
. ,
,  .
.


