

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1.Численное дифференцирование.
2.Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.
3.Погрешность в определении производной.
Дифференциал аргумента равен приращению аргумента 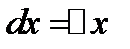 . Поэтому дифференциал функции равен произведению от производной на дифференциал аргумента
. Поэтому дифференциал функции равен произведению от производной на дифференциал аргумента 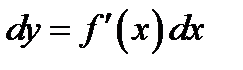 .
.
Рассмотрим функцию 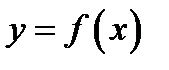 . Предположим, что величина
. Предположим, что величина 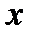 получена непосредственным измерением или в результате приближенного вычисления. Тогда при нахождении величины
получена непосредственным измерением или в результате приближенного вычисления. Тогда при нахождении величины 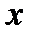 мы допускаем не зависящую от нас погрешность
мы допускаем не зависящую от нас погрешность 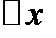 . Пусть
. Пусть 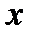 – приближенное значение аргумента,
– приближенное значение аргумента, 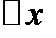 -абсолютная погрешность величины
-абсолютная погрешность величины 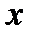 ,
, 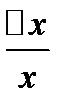 - относительная погрешность
- относительная погрешность
величины 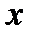 ,
, 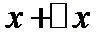 -истинное значение измеряемой величины. Тогда
-истинное значение измеряемой величины. Тогда 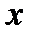 определяет приближенное значение
определяет приближенное значение 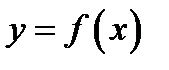 , а
, а 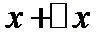 -ее истинное значение
-ее истинное значение 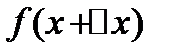 , откуда следует, что абсолютная погрешность функции
, откуда следует, что абсолютная погрешность функции 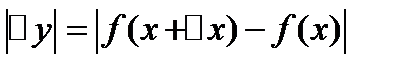 . При малых значениях
. При малых значениях 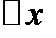 величину
величину 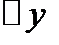 можно приближенно заменить дифференциалом
можно приближенно заменить дифференциалом 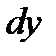 :
: 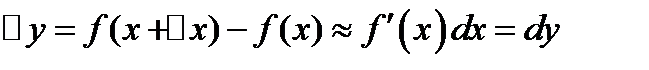 .
.
Выгода замены приращения функции 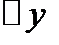 ее дифференциалом
ее дифференциалом 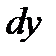 состоит в том, что
состоит в том, что 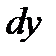 зависит от
зависит от 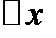 линейно, а
линейно, а 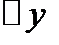 представляет собой обычно более сложную зависимость от
представляет собой обычно более сложную зависимость от 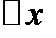 .
.
Полагая  , получим выражение для относительной погрешности
, получим выражение для относительной погрешности 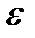 величины
величины 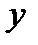
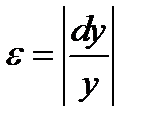 .
.
Пример: Найти абсолютную и относительную погрешность при замене приращения функции  ее дифференциалом в точке
ее дифференциалом в точке 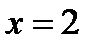 при
при 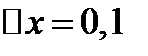 .
.
Решение.
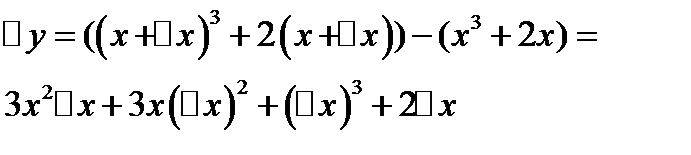
 ;
; 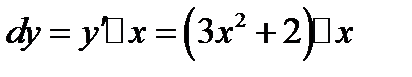 ;
;
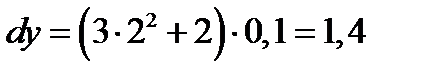 ;
; 
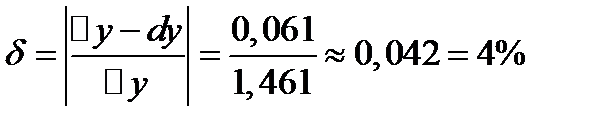
Вопросы для самопроверки:
1.В чем заключается смысл численного дифференцирования.
2.Что называется дифференциалом функции, чему он равен, как обозначается и каков его геометрический смысл?
3.Назовите формулу приближенного дифференцирования, основанные на интерполяционных формулах Ньютона.
4.Какая погрешность называется абсолютной?
5. Какая погрешность называется относительной?
|
|
Тема 3.3. Численное решение обыкновенных
Дифференциальных уравнений.
1.Метод Эйлера для решения задачи Коши.
Рассмотрим приближенное решение уравнения (1)  на отрезке
на отрезке  .удовлетворяющее начальному условию
.удовлетворяющее начальному условию  при
при  . Разделим отрезок
. Разделим отрезок  точками
точками  на
на 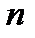 равных частей (здесь
равных частей (здесь  ). Обозначим
). Обозначим  , следовательно,
, следовательно, 
Пусть  есть некоторое приближенное решение уравнения(1) и
есть некоторое приближенное решение уравнения(1) и 
Обозначим 
В каждой из точек  в уравнении (1) производную заменим отношением конечных разностей: (2)
в уравнении (1) производную заменим отношением конечных разностей: (2)  ; (2.1)
; (2.1) 
При  будем иметь
будем иметь  ,
,  или
или 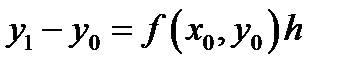
В этом равенстве  известны, следовательно находим
известны, следовательно находим 
При 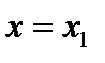 уравнение (2.1) примет вид
уравнение (2.1) примет вид  или
или  ;
;
 где
где  -известны. Аналогично находим
-известны. Аналогично находим
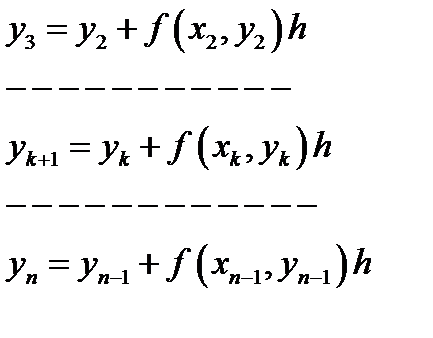
Т.О. приближенные значения решения в точках  найдены. Соединяя на координатной плоскости точки
найдены. Соединяя на координатной плоскости точки  отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.
отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.
Пример: При  найти приближенное значение решения уравнения у
найти приближенное значение решения уравнения у 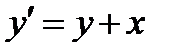 удовлетворяющего начальному условию
удовлетворяющего начальному условию  при
при  .
.
Решение
Разделим отрезок  на 10 равных частей точками
на 10 равных частей точками 
Следовательно,  значения
значения  будем искать по формуле (2.1)
будем искать по формуле (2.1) 
 или
или 
Таким образом, получаем 
В процессе решения составим таблицу

| 
| 
| 
|
 =0 =0
| 1,000 | 1,000 | 0,100 |
 =0,1 =0,1
| 1,100 | 1,200 | 0,120 |
 =0,2 =0,2
| 1.220 | 1,420 | 0.142 |
 =0,3 =0,3
| 1,362 | 1,620 | 0,162 |
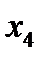 =0,4 =0,4
| 1,524 | 1,924 | 0,1924 |
 =0,5 =0,5
| 1,7164 | 2,2164 | 0,2216 |
 =0,6 =0,6
| 1.9380 | 2.5380 | 0.2538 |
 =0,7 =0,7
| 2,1918 | 2.8918 | 0,2892 |
 =0.8 =0.8
| 2.4810 | 3.2810 | 0.3281 |
 =0,9 =0,9
| 2,8091 | 3,7091 | 0,3709 |
 =1,0 =1,0
| 3,1800 |
Мы нашли приближенное значение

Точное решение данного уравнения, удовлетворяющее укзанным начальным условиям, будет

Следовательно
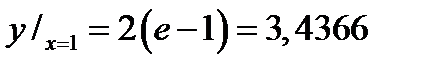
Вопросы для самопроверки:
1. В чем заключается метод Эйлера для решения задачи Коши?
Тема занятия: Численное решение обыкновенных дифференциальных уравнений (метод Эйлера для решения задачи Коши)
Рассмотрим приближенное решение уравнения (1)  на отрезке
на отрезке  .удовлетворяющее начальному условию
.удовлетворяющее начальному условию  при
при  . Разделим отрезок
. Разделим отрезок  точками
точками  на
на 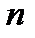 равных частей (здесь
равных частей (здесь  ). Обозначим
). Обозначим  , следовательно,
, следовательно, 
Пусть  есть некоторое приближенное решение уравнения(1) и
есть некоторое приближенное решение уравнения(1) и 
|
|
Обозначим 
В каждой из точек  в уравнении (1) производную заменим отношением конечных разностей: (2)
в уравнении (1) производную заменим отношением конечных разностей: (2)  ; (2.1)
; (2.1) 
При  будем иметь
будем иметь  ,
,  или
или 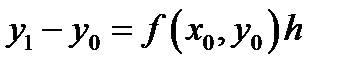
В этом равенстве  известны, следовательно находим
известны, следовательно находим 
При 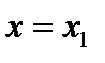 уравнение (2.1) примет вид
уравнение (2.1) примет вид  или
или  ;
;
 где
где  -известны. Аналогично находим
-известны. Аналогично находим
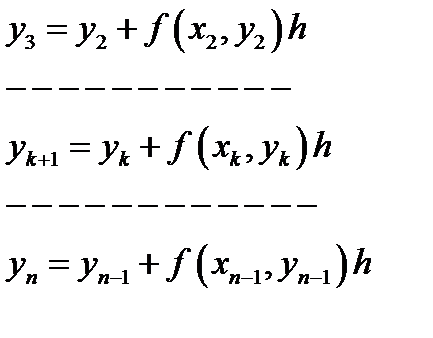
Т.О. приближенные значения решения в точках  найдены. Соединяя на координатной плоскости точки
найдены. Соединяя на координатной плоскости точки  отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.
отрезками прямой, получим ломаную - приближенное изображение интегральной кривой. Эта ломаная называется ломаной Эйлера.
Пример: При  найти приближенное значение решения уравнения у
найти приближенное значение решения уравнения у 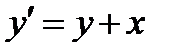 удовлетворяющего начальному условию
удовлетворяющего начальному условию  при
при  .
.
Решение
Разделим отрезок  на 10 равных частей точками
на 10 равных частей точками 
Следовательно,  значения
значения  будем искать по формуле (2.1)
будем искать по формуле (2.1) 
 или
или 
Таким образом, получаем 
В процессе решения составим таблицу

| 
| 
| 
|
 =0 =0
| 1,000 | 1,000 | 0,100 |
 =0,1 =0,1
| 1,100 | 1,200 | 0,120 |
 =0,2 =0,2
| 1.220 | 1,420 | 0.142 |
 =0,3 =0,3
| 1,362 | 1,620 | 0,162 |
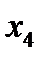 =0,4 =0,4
| 1,524 | 1,924 | 0,1924 |
 =0,5 =0,5
| 1,7164 | 2,2164 | 0,2216 |
 =0,6 =0,6
| 1.9380 | 2.5380 | 0.2538 |
 =0,7 =0,7
| 2,1918 | 2.8918 | 0,2892 |
 =0.8 =0.8
| 2.4810 | 3.2810 | 0.3281 |
 =0,9 =0,9
| 2,8091 | 3,7091 | 0,3709 |
 =1,0 =1,0
| 3,1800 |
Мы нашли приближенное значение

Точное решение данного уравнения, удовлетворяющее укзанным начальным условиям, будет

Следовательно
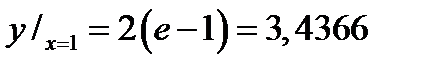
Контрольная работа
1.Материальная точка массой m кг движется прямолинейно по закону S(t).
Найти силу, действующую на нее в момент времени t.
Вариант 1 m= 2 кг 
 с;
с;
Вариант 2 m= 3 кг  (м)
(м)  с;
с;
Вариант 3 m= 4 кг 
 с.;
с.;
Вариант 4 m= 3 кг  (м)
(м)  с;
с;
Вариант 5 m= 2 кг  (м)
(м)  с;
с;
Вариант 6 m= 4 кг  (м)
(м) 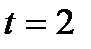 с;;
с;;
Вариант 7 m= 2 кг 
 с;
с;
Вариант 8 m= 2 кг 
 с;
с;
Вариант 9 m= 2 кг 
 с;
с;
Вариант 10 m= 2 кг 
 с;
с;
2. Вариант 1.Напишите уравнение касательной к графику функции  в точке
в точке  .
. 
Вариант 2. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 3. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 4. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 5. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 6. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
;  .
.
Вариант 7. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 8. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 9. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
Вариант 10. Напишите уравнение касательной к графику функции  в точке
в точке  .
.  ;
; 
3.Исследуйте функцию и постройте ее график:
|
|
Вариант 1.  Вариант 2.
Вариант 2.  ;
;
Вариант 3.  ; Вариант 4.
; Вариант 4.  ;
;
Вариант 5.  ; Вариант 6.
; Вариант 6.  ;
;
Вариант 7.  ; Вариант 8.
; Вариант 8.  ;
;
Вариант 9.  ; Вариант 10.
; Вариант 10.  .
.
4. Решите задачу:
Вариант 1.
Два тела движутся по прямой из одной и той же точки. Первое тело движется со скоростью  м/с, второе – со скоростью
м/с, второе – со скоростью  м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?
м/с. В какой момент и на каком расстоянии от начальной точки произойдет их встреча?
Вариант 2.
Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью  м/с, второе – со скоростью
м/с, второе – со скоростью  м/с. На каком расстоянии друг от друга они окажутся через 10 с?
м/с. На каком расстоянии друг от друга они окажутся через 10 с?
Вариант 3.
Скорость движения точки  м/с. Найдите путь, пройденный за 5 с. от начала движения.
м/с. Найдите путь, пройденный за 5 с. от начала движения.
Вариант 4.
Скорость движения точки  м/с. Найдите ее путь за 2-ю секунду.
м/с. Найдите ее путь за 2-ю секунду.
Вариант 5.
Скорость движения точки  м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.
м/с. Найдите путь, пройденный точкой от начала движения до ее остановки.
Вариант 6.
Скорость движения точки  м/с. Найдите: 1)Путь пройденный точкой за 3 с. от начала движения; 2)Путь пройденный точкой за 3-ю секунду.
м/с. Найдите: 1)Путь пройденный точкой за 3 с. от начала движения; 2)Путь пройденный точкой за 3-ю секунду.
Вариант 7.
Пружина растягивается на 0,02 м под действием силы 60 Н. Какую работу производит эта сила, растягивая пружину на 0,12?
Вариант 8.
Под действием силы 80 Н пружина растягивается на 0,02 м. Первоначальная длина пружины равна 0,15 м. Какую работу надо совершить, чтобы растянуть ее до 0,2 м.
Вариант 9.
Пружина в спокойном состоянии имеет длину 0,1 м. сила в 20 Н растягивает ее на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,12 до 0,14 м?
Вариант 10.
При сжатии пружины на 0,05 м совершается работа 30 Дж. Какую работу необходимо совершить чтобы сжать пружину на 0.08 м?
5. Найдите общие решения уравнений:
Вариант 1.  ; Вариант 2.
; Вариант 2.  ;
;
Вариант 3.  ; Вариант 4.
; Вариант 4.  ;
;
Вариант 5.  ; Вариант 6.
; Вариант 6.  ;
;
Вариант 7.  ; Вариант 8.
; Вариант 8.  ;
;
Вариант 9.  ; Вариант 10.
; Вариант 10. 
6. Используя признак Даламбера, исследуйте сходимость ряда:
Вариант 1.  ; Вариант 2.
; Вариант 2.  ;
;
Вариант 3. 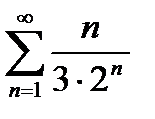 ; Вариант 4.
; Вариант 4.  ;
;
Вариант 5.  ; Вариант 6.
; Вариант 6. 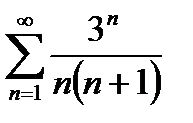 ;
;
Вариант 7.  ; Вариант 8.
; Вариант 8. 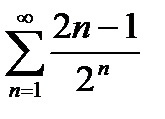 ;
;
Вариант 9. 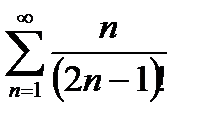 ; Вариант10.
; Вариант10.  .
.
7. Дискретная величина распределяется по закону.
1.Начертить график (т. е. построить многоугольник распределения):
2.Найти математическое ожидание:
3.Найти дисперсию и среднее квадратичное ожидание:
|
|
Вариант 1 Х 2 4 7 9 Вариант 2. Х 2 4 5 6
Р 0,1 0,6 0,2 0,1 Р 0,3 0,1 0,2 0,4
Вариант 3. Х 10 15 20 Вариант 4. Х 2 4 6
Р 0,1 0,7 0,2 Р 0,1 0,7 0,2
Вариант 5. Х 2 3 4 9 Вариант 6. Х 12 14 16
Р 0,3 0,1 0,2 0,4 Р 0,2 0,6 0,2
Вариант 7. Х 1 3 5 7 Вариант 8. Х 2 4 6 8
Р 0,3 0,1 0,2 0,4 Р 0,5 0,1 0,3 0,1
Вариант 9. Х 1 3 7 2 Вариант 10. Х 2 4 6
Р 0,3 0,1 0,2 0,4 Р 0,1 0,7 0,2
Методические указания
по изучению дисциплины Математика
для специальности 140414.51 Техническая эксплуатация
и обслуживание электрического
и электромеханического
оборудования (по отраслям)
Уровень подготовки базовый
Тольятти 2012
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!