Рекурсивные фильтры осуществляют обработку сигналов в соответствии с разностным уравнением и основными формами реализации фильтров являются: прямая (рис. 9.3), каноническая (рис. 9.4), каскадная (рис. 9.6) и параллельная (рис. 9.7).
РФ порядка выше второго (по числу полюсов N) реализуется, чаще всего, путем последовательного или параллельного соединения базовых звеньев второго порядка, что соответствует каскадной и параллельной формам реализации. Базовые звенья РФ выполняются в соответствии с прямой или канонической формами реализации РФ, (рис. 9.5).
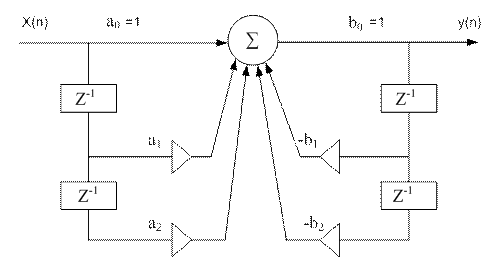
Рис. 9.5 Биквадратное звено
Число последовательных или параллельных звеньев k при четном порядке фильтра N находится как k =  , а при нечетном – как k =
, а при нечетном – как k =  , при этом одно звено фильтра является звеном первого порядка для него (a2=0, b2=0).
, при этом одно звено фильтра является звеном первого порядка для него (a2=0, b2=0).
Передаточная функция каскадной структуры РФ, (рис. 9.6) определяется как произведение передаточных функций всех звеньев.

Рис. 9.6 Каскадная структура РЦФ

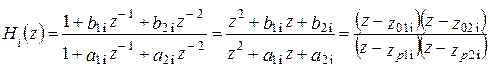 (9.9)
(9.9)
Здесь Hi(z) - передаточная функция i-го биквадратного звена (т.е звена второго порядка) при bоi = 1;
C0 – масштабирующий или нормирующий множитель. Входным сигналом i-го звена xi(n) в такой структуре является выходной сигнал yi-1(n) предыдущего звена: xi(n) = yi-1(n).
Последовательная форма реализации ЦФ часто используется на практике, поскольку она позволяет ослабить нежелательные эффекты, связанные с ошибками округления и коэффициенты получаются более однородные [4].
Коэффициенты звеньев РФ могут быть найдены через полюсы и нули передаточной функции следующим образом:

 (9.10)
(9.10)
Пары нулей и полюсов, определяющие значения коэффициентов i-го звена могут быть вещественными разными, равными, а при (b1i2 – 4b2i) < 0 и (a1i2 – 4a2i) < 0 – комплексно-сопряженными

В этом случае соотношения (9.10) примут вид:

 (9.11)
(9.11)
где Ωоi = ωоiТд, Ωpi = ωpiТд – нормированные частоты нулей и полюсов.
В случае звена первого порядка a1 = -zpi, b1 = -zоi.
Передаточная функция при параллельной форме реализации РФ (рис. 9.7) определяется суммой передаточных функций звеньев Hi(z), а также константы C0.
 (9.12)
(9.12)

Рис. 9.7 Параллельная структура РЦФ
Для звена первого порядка коэффициенты b1i = 0, a2i = 0.
Выходной сигнал фильтра будет определятся как сумма выходных сигналов всех звеньев:

Передаточная функция, для этой структуры РФ, получается разложением на простые дроби передаточной функции фильтра, представленной в полиномиальной или нуль-полюсной форме. А порядок числителя передаточной функции звеньев параллельной структуры Hi(z) (9.12) на единицу меньше порядка знаменателя этой функции. Коэффициенты a1i и a2i в формуле (9.12) определяются по тем же соотношениям, что и для каскадной формы реализации. Коэффициенты bоi и b1i связаны с нулями и полюсами фильтра через вычеты его передаточной функции в полиномиальной или нуль-полюсной форме, вычисляемых в полюсах передаточной функции zpi:
 (9.13)
(9.13)
А в случае комплексно-сопряженных полюсов zp1i=  = zpi выражение (9.13) преобразуется к виду:
= zpi выражение (9.13) преобразуется к виду:
 (9.14)
(9.14)
Сами вычеты в полюсах zpi могут быть найдены следующим образом:

i = 1, 2, …, N
Коэффициент C0 в выражении для передаточной функции связан с нулями и полюсами фильтра и может быть определен так  .
.
Однако коэффициенты Co, boi, b1i могут быть выражены через коэффициенты каскадной формы реализации ЦФ, которые связаны с полюсами и нулями фильтра более простой зависимостью. Остальные формы реализации используются реже, и с ними можно познакомиться в соответствующей литературе [1, 2].






 , а при нечетном – как k =
, а при нечетном – как k =  , при этом одно звено фильтра является звеном первого порядка для него (a2=0, b2=0).
, при этом одно звено фильтра является звеном первого порядка для него (a2=0, b2=0).

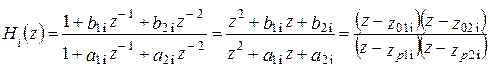 (9.9)
(9.9)
 (9.10)
(9.10)

 (9.11)
(9.11) (9.12)
(9.12)

 (9.13)
(9.13) = zpi выражение (9.13) преобразуется к виду:
= zpi выражение (9.13) преобразуется к виду: (9.14)
(9.14)
 .
.


