Переходим к рассмотрению типового задания.
Пример: Найти область сходимости степенного ряда 
Решение: Задание часто формулируют эквивалентно: Найти интервал сходимости степенного ряда и исследовать его сходимость на концах найденного интервала.
1) На первом этапе находим радиус сходимости ряда по формуле:
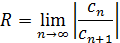

2) Записываем интервал сходимости ряда  :
:
 .
.
3) Проверяем сходимость ряда на концах интервала:
а) Рассматриваем правый конец интервала  , подставляем это значение в наш степенной ряд
, подставляем это значение в наш степенной ряд  :
:
При  – сходится (случай обобщенного гармонического ряда).
– сходится (случай обобщенного гармонического ряда).
б) Берём левый конец интервала  и подставляем его в наш степенной ряд
и подставляем его в наш степенной ряд  :
:
При 
Получен числовой знакочередующийся ряд, и нам нужно исследовать его на сходимость.
Используем признак Лейбница:
1) Члены ряда убывают по модулю: каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно – первое условие выполняется.
2)  – второе условие выполняется.
– второе условие выполняется.
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость:
 – сходится (случай обобщенного гармонического ряда).
– сходится (случай обобщенного гармонического ряда).
Таким образом, полученный числовой ряд сходится абсолютно.
Таким образом, степенной ряд  сходится на обоих концах найденного интервала.
сходится на обоих концах найденного интервала.
Ответ: Область сходимости исследуемого степенного ряда: 
Имеет право на жизнь и другое оформление ответа: Ряд сходится, если 
!!! Иногда в условии задачи требуют указать радиус сходимости. Очевидно, что в рассмотренном примере  .
.
Пример: Найти область сходимости ряда  .
.
Решение: Найдем радиус сходимости данного ряда.

Итак, ряд сходится при 
Раскрываем модуль:

И прибавляем ко всем частям единицу:

 – интервал сходимости исследуемого степенного ряда.
– интервал сходимости исследуемого степенного ряда.
Исследуем сходимость степенного ряда на концах найденного интервала:
1) Если x=-8, то получается следующий числовой ряд:
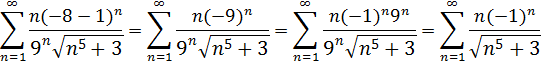
Получен числовой знакочередующийся ряд, и нам нужно исследовать его на сходимость.
Используем признак Лейбница:
1) Члены ряда убывают по модулю: каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно – первое условие выполняется.
2)  – второе условие выполняется.
– второе условие выполняется.
Вывод: ряд сходится.
Исследуем ряд на абсолютную сходимость.
Составим ряд из абсолютных членов:
 .
.
По всем признакам для полученного числового ряда  следует применить предельный признак сравнения.
следует применить предельный признак сравнения.
Определяем старшую степень знаменателя, для этого мысленно или на черновике отбрасываем под корнем всё, кроме самого старшего слагаемого:  . Таким образом, старшая степень знаменателя равна
. Таким образом, старшая степень знаменателя равна 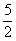 . Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:
. Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:  .
.
Таким образом, наш ряд нужно сравнить со сходящимся рядом  .
.
Используем предельный признак сравнения:
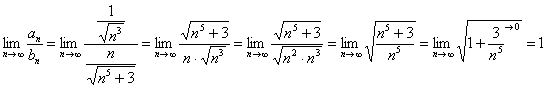
Получено конечное, отличное от нуля число, значит, ряд  сходится вместе с рядом
сходится вместе с рядом  .
.
Таким образом, полученный числовой ряд сходится абсолютно.
2) Что происходит на другом конце интервала?
При x=10. Получаем ряд
 – сходится (Получился точно такой же числовой ряд, сходимость которого мы только что доказали).
– сходится (Получился точно такой же числовой ряд, сходимость которого мы только что доказали).
Ответ: область сходимости исследуемого степенного ряда:
 или
или 






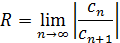

 :
: .
. , подставляем это значение в наш степенной ряд
, подставляем это значение в наш степенной ряд  – сходится (случай обобщенного гармонического ряда).
– сходится (случай обобщенного гармонического ряда). и подставляем его в наш степенной ряд
и подставляем его в наш степенной ряд 
 – второе условие выполняется.
– второе условие выполняется. – сходится (случай обобщенного гармонического ряда).
– сходится (случай обобщенного гармонического ряда).

 .
. .
.



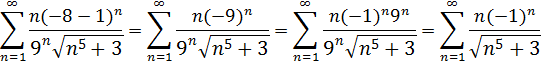
 – второе условие выполняется.
– второе условие выполняется. .
. . Таким образом, старшая степень знаменателя равна
. Таким образом, старшая степень знаменателя равна 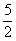 . Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:
. Старшая степень числителя, очевидно, равна 1. Из старшей степени знаменателя вычитаем старшую степень числителя:  .
. .
.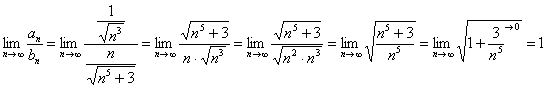
 .
. – сходится (Получился точно такой же числовой ряд, сходимость которого мы только что доказали).
– сходится (Получился точно такой же числовой ряд, сходимость которого мы только что доказали). или
или 



