

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Введение
Исследование - универсальный способ познания действительности, который помогает развитию личности в динамично изменяющемся мире. Руководство научно-исследовательской деятельностью школьников - одно из направлений в работе современного учителя. Организация данного вида деятельности опирается на ряд условий. И главным из них можно считать наличие у педагога и учащегося общей точки соприкосновения в какой-либо области, интересной для исследования. Именно отсутствие этого общего интереса делает многие темы научной работы бесперспективными.
Исследовательская и проектная деятельность учащихся является результативным способом достижения одной из важнейших целей образования: научить детей самостоятельно мыслить, ставить и решать проблемы, привлекая знания из разных областей; уметь прогнозировать вариативность результатов.
Организация и дальнейшее развитие научно-исследовательской работы школьников - одна из основных форм творческой работы с молодежью. Она требует применения современных информационных технологий, обеспечивающих доступ к необходимым профильным базам, банкам данных, источникам информации по теме исследования.
Как показывает опыт, метод проектов и деятельностный подход к обучению как нельзя лучше решают задачи новой школы. Раннее приобщение детей к научно-исследовательской и поисковой деятельности позволяет наиболее полно определять и развивать интеллектуальные и творческие способности, причем не только в старшей школе, но и в начальной. Исследовательская работа обучающихся как самостоятельный вид учебной деятельности осуществляется на всех уровнях образовательной системы в разном объёме.
|
|
Сейчас в РБ сложилась и успешно действует практика научно-практических конференций, на которых юные исследователи выступают с сообщениями об исследованиях, выполненных самостоятельно или под руководством школьных учителей, преподавателей вузов, научных сотрудников институтов. Подобные мероприятия не замыкаются в рамках страны, а выходят международный уровень.
Цель данной работы - создать т. н. пособие для учителей и студентов, желающих заниматься данным видом творческой работы со школьниками.
Исследовательская деятельность учащихся во многих учреждениях становится средством интеграции образовательных программ общего среднего и дополнительного образования. Это позволяет объединять преимущества, свойственные образовательным программам этих двух типов: ориентированность общего среднего образования на выполнение государственного и социального заказа общества на воспроизводство профессионально-кадрового потенциала и направленность дополнительного образования на свободный выбор ребенком и его семьей видов и форм деятельности, формирование его собственных представлений о мире, развитии познавательной мотивации, способностей и склонностей.
Работа состоит из 3 разделов. В первом разделе идет речь о формах и содержании научно-исследовательской работы школьников в РБ, приведены примеры (Республиканская летняя научно-исследовательская школа учащихся и учителей, турнир юных математиков). Второй раздел посвящен методам и приемам научно-исследовательской деятельности школьников, а именно: неполная индукция, обобщение, аналогия, специализация. В третьем разделе представлены примеры задач исследовательского характера.
1. Научно-исследовательская работа школьников в РБ. Формы и содержание
Турнир юных математиков
Турнир юных математиков - командные соревнования учащихся в умении решать исследовательские задачи, убедительно представлять полученные результаты и аргументировано отстаивать свою точку зрения в публичных дискуссиях.
|
|
Основные цели турнира состоят в привлечении учащихся к исследовательской работе и привитии им навыков проведения научных исследований, представления и защиты своих результатов, ведения научной дискуссии. Задачами турнира являются:
популяризация новых форм работы с талантливой молодежью;
развитие и укрепление контактов между учреждениями образования, способными учащимися, учителями, преподавателями вузов и учеными республики и других стран;
обмен опытом в сфере дополнительного образования, изучение и использование лучших форм и методов внеклассного обучения, апробированного и используемого в различных странах;
привлечение ведущих ученых и преподавателей вузов к дополнительному образованию учащихся, предоставление талантливым школьникам благоприятных возможностей для общения с ними и получения советов и консультаций профессионального и профориентационного характера.
Организацию и проведение турнира осуществляет организационный комитет (далее - оргкомитет). Состав оргкомитета утверждается Министерством образования. Оргкомитет определяет и утверждает состав специального жюри, обеспечивающего подготовку заданий, отбор команд, судейство и правильность ведения соревнований.
Информационное сообщение о проведении турнира и условия заданий публикуются в республиканской периодической печати не менее чем за два месяца до начала турнира.
К участию в турнире юных математиков допускаются команды учащихся старших классов общеобразовательных учреждений, а также учащихся профессионально-технических или средних специальных учреждений образования. Кроме команд-участниц на турнир могут приглашаться наблюдатели.
Команда - участник турнира может либо представлять одно учреждение образования, либо быть сборной города, района или нескольких учреждений образования. Не допускается участие в турнире двух и более команд от одного учреждения образования, а также включение учащихся одного учреждения образования в две и более команд.
В состав команды может входить не более шести учащихся. Команду возглавляет капитан, назначаемый из числа участников команды. Каждая команда должна сопровождаться руководителем, который является официальным представителем соответствующего учреждения образования на турнире и несет ответственность за все действия команды во время проведения турнира.
|
|
Общий порядок проведения турнира зависит от числа участвующих команд. При наличии не менее 9 команд, он определяется следующим расписанием:
| 1-й день | Конкретные даты см. в Приложении В | Открытие турнира и жеребьевка отборочных боев первого тура | См. пп.8,16 | |
| 2-й день | Письменный (нулевой) тур | См. п.10 | ||
| 3-й день | Отборочные бои первого тура | См. пп.8,11,13 | ||
| 4-й день | Отборочные бои второго тура | См. пп.8,11,13 | ||
| 5-й день | Финальные бои (основной и малый финалы) | См. пп.8,11,14 | ||
| Закрытие турнира |
Для планирования турнира и разрешения спорных ситуаций, возникающих при его проведении, используется корректируемый рейтинг команд.
Рейтинг каждой команды - это величина, аккумулирующая результаты, полученные командой в ходе турнира, и призванная отражать ее относительную силу в ряду других участников. Он вычисляется по следующим правилам:
На основе рассмотрения предварительных материалов (см. п.4) каждая команда получает свой предварительный рейтинг Rпредв, который определяется следующим образом: суммируются баллы команды за все решения (находится сумма баллов команды Sком), после этого по суммарным баллам всех команд, приглашенных на турнир, вычисляется средний балл Sср и предварительный рейтинг каждой команды
Rпредв = 0,5· Sком/ Sср.
После проведения письменного (нулевого) тура происходит корректировка рейтингов команд. Для этого определяется приращение рейтинга каждой команды за нулевой тур R0, равный отношению суммы баллов команды к среднему баллу всех команд, набранных в письменном туре. Скорректированный рейтинг команды равен:
R: = Rпредв + R0.
После подведения итогов боя для каждой команды, участвовавшей в нем, производится корректировка текущего рейтинга. Для этого по итоговым суммам баллов всех команд (Sк, см. п. 20.2) находится средний итоговый балл команд в этом бою Sбоя и приращение рейтинга каждой команды, равное отношению Sк/ Sбоя. Приращения рейтингов команд, полученные ими в отборочных боях первого и второго тура и в финальных боях, обозначаются соответственно: R1, R2, Rф. Скорректированные рейтинги, которые становятся после пересчета текущими, вычисляются по правилам:
|
|
после отборочных боев первого тура:
R: = Rпредв + R0 + R1, после отборочных боев второго тура:
R: = Rпредв + R0 + R1 + R2, после финальных боев (основного и малого финала):
R: = Rпредв + R0 + R1 + R2 + Rф.
Победителями турнира юных математиков (первое, второе и третье место) признаются команды, занявшие соответствующие места в финальном бое. Победители турнира награждаются дипломами Министерства образования соответствующих степеней.
Победителям малого финала (командам, занявшим в малом финале первое, второе и третье места) присуждаются соответствующие места, непосредственно следующие за местами команд - участников основного финала. Победители малого финала награждаются грамотами специального жюри.
Кроме этого, отдельные команды и участники могут быть отмечены поощрительными свидетельствами или похвальными отзывами.
Математический бой - главная составная часть турнира юных математиков. Под математическим боем понимается организованная дискуссия нескольких команд, в которой каждая участвующая команда поочередно выступает в качестве докладчика своих результатов, оппонента по выступлению докладывавшей команды и рецензента, оценивающего качество дискуссии двух других команд.
Команды,участвующие в математическом бое, называются участниками боя. Как правило, число команд-участников боя три или четыре (в исключительных случаях возможно участие пяти или шести команд в одном бое, см. пп.7 и 8). Все участники боя образуют состав боя.
Математический бой состоит из нескольких раундов, в каждом из которых обсуждается одна задача, отличная от задач других раундов. Количество раундов совпадает с числом команд, участвующих в этом бое. В каждом раунде команда-участник исполняет только одну из ролей: Докладчика (Д), Оппонента (О), Рецензента (Р) или Наблюдателя (Н1, Н2 или Н3) (см. п. 19). Оппонент, Рецензент и Наблюдатели называются оппонирующими командами (участниками). Смена ролей команд в последовательных раундах определяется циклической перестановкой в ряду "Д, Н3, Н2, Н1, Р, О". В наиболее полном случае шестикомандного боя эта смена определяется следующей таблицей:
| Раунд → | 1 | 2 | 3 | 4 | 5 | 6 |
| Команда 1 | Д | Н3 | Н2 | Н1 | Р | О |
| Команда 2 | О | Д | Н3 | Н2 | Н1 | Р |
| Команда 3 | Р | О | Д | Н3 | Н2 | Н1 |
| Команда 4 | Н1 | Р | О | Д | Н3 | Н2 |
| Команда 5 | Н2 | Н1 | Р | О | Д | Н3 |
| Команда 6 | Н3 | Н2 | Н1 | Р | О | Д |
Первое место в математическом бое присуждается команде, имеющей наибольшую итоговую сумму баллов за бой. Последующие места присуждаются командам с меньшими итоговыми суммами баллов в порядке убывания.
|
|
Если расхождение итоговых сумм баллов двух или более команд невелико, должна быть вычислена относительная разность итоговых баллов этих команд, равная разности их баллов, выраженной в процентах от наибольшей итоговой суммы баллов в этом бое. Если относительная разность итоговых баллов команд не превосходит 5%, им присуждается одинаковое место в бое.
Если первое место в бою присуждено только одной команде, то такое первое место называется единоличным, а команда, занявшая его, считается одержавшей в этом бою чистую победу.
Неполная индукция
Неполная индукция - тип индуктивных умозаключений, посылки которых являются единичными суждениями, содержащими эмпирические данные об исследованных объектах некоторой области, а заключение - общим суждением обо всех предметах данной области или о некоторых, неисследованных предметах этой же. Доказательная сила Неполной индукции ограничена, поскольку связь между её посылками и заключением носит вероятностный, проблематичный характер. И тем не менее, именно Неполная индукция есть основной путь получения новых знаний, в отличие от так называемой полной индукции, посылки и заключение которой содержат в точности одну и ту же информацию.
Неполная индукция - индуктивный вывод о том, что всем представителям изучаемого множества принадлежит свойство Р на том основании, что Р принадлежит некоторым представителям этого множества. Так, напр., узнав о том, что инженер А работает продавцом, инженер B работает продавцом и инженер С также работает продавцом, вы можете сделать индуктивный вывод, что все инженеры ныне работают продавцами. Множество инженеров велико, трудно или даже невозможно установить, чем сейчас занимается каждый из них, поэтому ваше индуктивное заключение связано с риском: оно может оказаться ошибочным.
Неполная индукция дает вероятностное заключение и применяется при невозможности рассмотрения всех без исключения случаев. К неполной индукции относится перечислительная, аналитическая, научная.
Перечислительная (популярная) индукция осуществляется на основании повторяемости одного и того же признака у ряда факторов и отсутствия противоречивого случая, выводом что, все факторы этого рода имеют указанный признак. Так, обнаруживая массу у всех известных ему предметов, Ньютон обобщил: "Все тела имеют массу". Но подобные обобщения не всегда правомерны. Примером поспешного обобщения служат лебеди: европейцы считали что, все лебеди белые, пока не обнаружили в Австралии черных. Поскольку перечислительная индукция допускает исключения из правил, ее выводы лишь правдоподобны, а не достоверны. Уверенность в их истинности растет с появлением новых подтверждений, но утверждение ее возможно лишь через другие способы умозаключений.
Аналитическая индукция с целью исключить случаи поспешного обобщения предполагает выбор наиболее типичных факторов, разнородных по времени и другим возможным условиям. Например, о качестве партии товара судят по образцам из разных вагонов и разных мест вагона (при перечислительной индукции, проверяющие полностью проверили бы 2 вагона из 50 и, уморившись, решили бы: "Да че там проверять - вся партия такая!" - а в следующем вагоне могла бы начаться другая картина).
Научная индукция обобщает путем отбора необходимых и исключения случайных обстоятельств, учитывая важнейшую из необходимых связей - причинную и, при условии что, выбранная связь сочтена причинной не ошибочно, дает абсолютно достоверную информацию обо всех явлениях, какого либо класса на основании изучения некоторого их числа. При этом возможность установления причинной связи обусловлена тем что, если достоверно известно что, во всяких ситуациях, при всяких стечениях обстоятельств, только одно, в своем отличии, необходимо для отличия в исследуемом явлении, то оно и есть его причина.
Обобщение
Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Например, мы делаем обобщение, когда переходим от рассмотрения треугольников к рассмотрению многоугольников с произвольным числом сторон. Мы делаем обобщение и когда переходим от изучения тригонометрических функций острого угла к изучению тригонометрических функции произвольного угла.
Обобщение - как метод научного познания, во-первых, логический процесс перехода от единичного к общему, от менее общего к более общему знанию, установления общих свойств и признаков предметов, во-вторых, - результат этого процесса: обобщенное понятие, суждение, закон, теория. Получение обобщенного знания означает более глубокое отражение действительности, проникновение в ее сущность. Принято различать два вида научных обобщений: выделение любых признаков (абстрактно-общее) или существенных (конкретно-общее, т.е. закон).
По другому основанию можно выделить обобщения:
а) от отдельных фактов, событий к их выражению в мыслях (индуктивное обобщение);
б) от одной мысли к другой, более общей мысли (логическое обобщение). Мысленный переход от более общего к менее общему есть процесс ограничения.
Обобщение не может быть беспредельным. Его пределом являются философские категории, которые не имеют родового понятия и потому обобщить их нельзя.
Аналогия
Аналогия есть некоторого рода сходство. Она, можно сказать, есть сходство, но на более определенном и выражаемом с помощью понятий уровне. Однако мы можем выразиться несколько более точно. Существенное различие между аналогией и другими видами сходства заключается, как мне кажется, в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении. Если вы намереваетесь свести это отношение, в котором они согласуются, к определенным понятиям, то вы рассматриваете эти сходные предметы как аналогичные. Если вам удается добраться до ясных понятий, то вы выяснили аналогию.
Сравнивая молодую женщину с цветком, поэты ощущают, я надеюсь, некоторое сходство, но обычно они не имеют в виду аналогии. Действительно, они едва ли намериваются покинуть мир эмоций и свести это сравнение к чему-то измеримому или определимому с помощью понятий.
Рассматривая в музее естественной истории скелеты различных млекопитающих, вы можете обнаружить, что все они страшны. Если в этом все сходство, которое вы между ними обнаружили, то вы видите не такую уж сильную аналогию. Однако вы можете подметить удивительно много говорящую аналогию, если рассмотрите руку человека, лапу кошки, переднюю ногу лошади, плавник кита и крыло летучей мыши - эти столь различно используемые органы, как состоящие из сходных частей, имеющих сходное отношение друг к другу.
Аналогия есть умозаключение о принадлежности единичному явлению определенного признака на основе сходства этого явления в существенных признаках с другим уже известным единичным явлением. Она рассматривается в качестве разновидности индукции.
Приведем следующий пример умозаключения по аналогии: Для существования живых существ необходимы вода, воздух, соответствующая температура и т.д. На Марсе есть вода, воздух, соответствующая температура и т.д. Следовательно, на Марсе, возможно, существуют живые существа. Поскольку в данном силлогизме содержится ошибка, заключающаяся в том, что среднее понятие не распределено (ложность нераспределенного среднего термина), ценность заключения находится на уровне вероятности. Однако если среднее понятие будет распределенным (то есть, если будут установлены все условия, необходимые для существования живых существ), то и заключение станет определенным.
Другими словами, аналогия - это подобие, сходство предметов или явлений в каких-либо свойствах, признаках, отношениях, причем сами эти предметы, вообще говоря, различны. В математике часто рассматривают умозаключение по аналогии, сходству отдельных свойств (признаков) при сравнении двух множеств (фигур, отношений, объектов и т.д.).
Аналогия весьма доступна и проста как прием рассуждения, но она в первую очередь позволяет выдвинуть гипотезу, которую потом требуется строго доказать.
Специализация
Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном.
Например, мы специализируем, когда переходим от рассмотрения многоугольников к рассмотрению правильных многоугольников, п специализируем еще дальше, когда переходим от правильных многоугольников с п сторонами к правильному, т.е. равностороннему треугольнику.
Эти два последовательных перехода осуществлялись в двух характерно различных направлениях. В первом переходе, от многоугольников к правильным многоугольникам, мы ввели ограничение, именно потребовали, чтобы все стороны и все углы многоугольника были равны. Во втором переходе мы заменили переменный предмет конкретным, поставили 3 вместо переменного целого числа п.
Очень часто мы производим специализацию, переходя от целого класса предметов к одному предмету, содержащемуся в этом классе. Например, когда мы хотим проверить некоторое общее утверждение относительно простых чисел, мы выбираем какое-нибудь простое число, скажем 17, и исследуем, справедливо ли это общее утверждение или нет именно для этого числа 17.
Пример задачи исследовательского характера для школьников
Пример 1: неприводимые многочлены
Многочлен h (x) с целыми коэффициентами положительной степени называется неприводимым, если он не представим в виде произведения двух многочленов положительных степеней с целыми коэффициентами.
Пусть g (x) = (x - a 1) … (x - an), где a 1,…, an - различные целые числа.
Пусть f (x) = mx +1, где m - целое число. Найдите все значения m, для которых многочлен f (g (x)) неприводим.
Пусть f (x) = mx 2+1, где m - натуральное число. Докажите, что многочлен f (g (x)) неприводим.
Исследуйте неприводимость многочленов вида f (g (x)) для других неприводимых многочленов f (x) (например, для неприводимых квадратичных многочленов ax 2+ bx +1).
Решение.
1. Предположим, что многочлен f (g (x)) приводим, то есть для некоторых двух многочленов f 1 (x) и f 2 (x) положительной степени с целыми коэффициентами
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x).
Это верно для всех x, в том числе и для x = a 1, …, x = an. Получаем,
f 1 (a 1) f 2 (a 1) =1,…,
f 1 (an) f 2 (an) =1.
Рассмотрим первое из этих равенств. Оно возможно для целого a 1 и многочленов f 1 (x), f 2 (x) с целыми коэффициентами только если f 1 (a 1) = f 2 (a 1) =1 или f 1 (a 1) = f 2 (a 1) =-1. Аналогично и для остальных равенств. Пусть в i случаях будет 1, в j будет - 1. Тогда i + j = n.
Покажем, что n - четное и i = j =  . Допустим, что i >
. Допустим, что i > 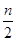 (т.е. j = n - i <
(т.е. j = n - i < 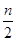 ). Тогда многочлены f 1 (x) - 1 и f 2 (x) - 1 имеют не менее i корней, а, следовательно, их степень больше
). Тогда многочлены f 1 (x) - 1 и f 2 (x) - 1 имеют не менее i корней, а, следовательно, их степень больше  . Поэтому и степени многочленов f 1 (x) и f 2 (x) соответственно больше
. Поэтому и степени многочленов f 1 (x) и f 2 (x) соответственно больше 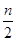 . Таким образом степень f 1 (x) f 2 (x) = m (x - a 1) … (x - an) +1 больше n. Противоречие показывает, что допущенное не верно. Аналогично, j не больше
. Таким образом степень f 1 (x) f 2 (x) = m (x - a 1) … (x - an) +1 больше n. Противоречие показывает, что допущенное не верно. Аналогично, j не больше 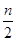 .
.
Два числа не превосходящие  в сумме дают n. Значит, i = j =
в сумме дают n. Значит, i = j = 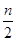 и n - четное число. При этом степени f 1 (x) и f 2 (x) также равны i =
и n - четное число. При этом степени f 1 (x) и f 2 (x) также равны i =  , иначе, рассуждая как и выше, получим противоречие.
, иначе, рассуждая как и выше, получим противоречие.
Не ограничивая общности, можно считать, что f 1 (a 1) =…= f 1 (ai) =1, f 1 (ai +1) =…= f 1 (an) =-1. (При перестановке местами a k и a l условие задачи не изменится, поэтому можно считать, что изначально их порядок такой, что f 1 (x) обращается в 1 в первых i). Тогда f 1 (x) = t 1× (x - a 1) … … (x - ai) +1 = t 2× (x - ai +1) … (x - an) -1. Аналогично, f 2 (x) = d 1× (x - a 1) … (x - ai) +1 = d 2× (x - ai +1) … (x - an) -1.
Рассмотрим равенства
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x) = (t 1× (x - a 1) … (x - ai) +1) × (d 1× (x - a 1) … (x - ai) +1);
m (x - a 1) … (x - an) +1 = f 1 (x) f 2 (x) = (t 1× (x - a 1) … (x - ai) +1) × (d 2× (x - ai +1) … (x - an) -1).
Приравнивая коэффициенты при старшей степени (xn) левой и правой части, получаем m = t 1 d 1 и m = t 1 d 2. Отсюда d 1 = d 2. Аналогично получаем, что t 1 = t 2. Таким образом, получаем, что m = t × d для некоторых целых t и d, причем:
f 1 (x) = t × (x - a 1) … (x - ai) +1 = t × (x - ai +1) … (x - an) -1
f 2 (x) = d × (x - a 1) … (x - ai) +1 = d × (x - ai +1) … (x - an) -1.
Вычтем из первого равенства второе
t × (x - a 1) … (x - ai) - d × (x - a 1) … (x - ai) = t × (x - ai +1) … (x - an) - d × (x - ai +1) … (x - an),
откуда, преобразовывая, получим
t × ((x - a 1) … (x - ai) - (x - ai +1) … (x - an)) = d × ((x - a 1) … (x - ai) - (x - ai +1) … (x - an)).
Это равенство выполнено для всех x, поэтому можно считать, что
(x - a 1) … (x - ai) - (x - ai +1) … (x - an) ¹ 0, и t = d.
Таким образом,
f 1 (x) = f 2 (x) = t × (x - a 1) … (x - ai) +1 = t × (x - ai +1) … (x - an) -1.
Применим к этому равенству обобщенную теорему Виета и рассмотрим свободные члены
(-1) i × t × a 1×…× ai +1 = (-1) i × t × ai +1×…× an -1.
Перенесем слагаемые с t влево, без t вправо. Вынесем t за скобки
t × (a 1×…× ai - ai +1×…× an) = ±2.
Выражение в скобках - целое число. Поэтому t может принимать только 4 различные значения: ±1 и ±2. Но как показано выше, m = t × t. Следовательно только для двух целых значений m многочлен f (g (x)) приводим. Это m = 1 и m = 4.
Приведем примеры приводимых многочленов для этих m.
(x -1) (x -2) (x -3) (x -4) + 1 = ((x -1) (x -4) +1) × ((x -2) (x -3) -1)
Действительно, ((x -1) (x -4) +1) × ((x -2) (x -3) -1) = (x -1) (x -2) (x -3) (x -4) - x 2+5 x - 4 + x 2 - 5 x +6-1= = (x -1) (x -2) (x -3) (x -4) + 1.
Для m = 4
4 x (x -1) +1 = 4 x 2 - 4 x + 1 = (2 x -1) (2 x -1)
Ответ: f (g (x)) неприводим при всех целых m Ï{1; 4}.
2. Допустим, что m (x - a 1) 2… (x - an) 2+1 приводим, тогда
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) f 2 (x).
Как и выше, f 1 (x) = f 2 (x) =1 либо f 1 (x) = f 2 (x) = - 1 для всех x из { a 1; …; an }. Если f 1 (x) принимает значения и 1 и - 1, то в силу непрерывности многочлена, f 1 (x) = 0 для некоторого x. Но тогда для этого x выполнено равенство
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) f 2 (x) = 0,
чего быть не может ни при одном натуральном m. Поэтому для определенности будем считать, что f 1 (ai) = f 2 (ai) =1 для всех i от 1 до n. (В случае, когда, f 1 (ai) = f 2 (ai) =-1 для всех i от 1 до n доказательство проводится аналогично) Как и в пункте 1, получаем
f 1 (x) = t × (x - a 1) … (x - an) +1;
f 2 (x) = d × (x - a 1) … (x - an) +1.
Отсюда,
m (x - a 1) 2… (x - an) 2+1 = f 1 (x) × f 2 (x) = t × d × (x - a 1) 2… (x - an) 2+ (t + d) × (x - a 1) … (x - an) +1.
Из равенства многочленов получаем m = t × d и (t + d) × (x - a 1) … (x - an) = 0. Последнее равенство выполнено при всех значениях x, поэтому из него следует, что t + d = 0, то есть t = - d. Откуда натуральное m = - t 2. Противоречие показывает, что многочлен m (x - a 1) 2… (x - an) 2+1 неприводим. Утверждение доказано.
3. Рассмотрим неприводимый многочлен ax 2+ bx +1. Допустим, дискриминант b 2-4 a <0, а многочлен a × (x - a 1) 2… (x - an) 2 + b × (x - a 1) … (x - an) +1 = f 1 (x) × f 2 (x) приводим. Как и в пункте 2, учитывая, что при отрицательном дискриминанте многочлен не будет обращаться в 0, получаем:
f 1 (x) = t × (x - a 1) … (x - an) +1;
f 2 (x) = d × (x - a 1) … (x - an) +1.
Отсюда,
a × (x - a 1) 2… (x - an) 2 + b × (x - a 1) … (x - an) +1 =
= f 1 (x) × f 2 (x) = t × d × (x - a 1) 2… (x - an) 2+ (t + d) × (x - a 1) … (x - an) +1.
Из равенства многочленов получаем, что a = t × d и b = t + d. Значит t и d являются корнями уравнения x 2 - bx + a = 0. Но согласно предположению дискриминант этого уравнения b 2-4 a <0. Уравнение не имеет корней. Таким образом допущение не верно и при отрицательном дискриминанте многочлен a × (g (x)) 2+ b × g (x) +1 неприводим.
Пример 2: волнистые числа
Назовем девятизначное число  волнистым числом первого типа, если
волнистым числом первого типа, если


Например, число 162539581 волнистое число первого типа. Назовем девятизначное число волнистым числом второго типа, если


а) Найдите количество девятизначных волнистых чисел первого и второго типа.
б) Найдите формулу для вычисления количества волнистых п -значных чисел первого и второго типа.
Назовем девятизначное число  волнистым числом третьего типа, если
волнистым числом третьего типа, если


Назовем девятизначное число волнистым числом четвертого типа, если


а) Найдите количество девятизначных волнистых чисел третьего и четвертого типа.
б) Найдите формулу для вычисления количества волнистых п -значных чисел третьего и четвертого типа.
Предложите свои обобщения этой задачи и исследуйте их.
Решение
Лемма 1. Обозначим через f (n, k 1, k 2) - количество n -значных волнистых чисел первого типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2, g (n, k 1, k 2) - количество n -значных волнистых чисел второго типа, начинающихся с цифры k 1 и заканчивающиеся на цифру k 2. Тогда
 и
и
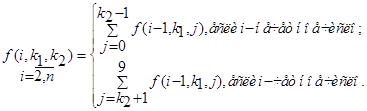
Также,  и
и

Доказательство. Рассмотрим n -значные волнистые числа первого типа.
Нетрудно заметить, как они получаются. Берутся все n -1-значные волнистые числа и, в зависимости от текущего знака (“<" или ”>”), дописывается каждому числу цифра, меньшая или большая последней, т.е. чтобы найти количество n -значных волнистых чисел, заканчивающихся на k, надо найти сумму всех количеств n -1-значных чисел заканчивающихся на цифры от 0 до k- 1 или от k +1 до 9.Т. к. на каждом шаге мы корректно вычисляем волнистые числа, то нет необходимости знать всё число: все зависит от последней цифры.
Следовательно, можно составить рекуррентную формулу, которая будет корректно вычислять количество n -значных волнистых чисел первого типа начинающихся на цифру k 1 и заканчивающихся на цифру k 2.
Рассмотрим рекуррентную формулу для волнистых чисел первого типа.
Начальные её значения 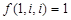 , т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i (
, т.е. есть только по одному однозначному волнистому числу, начинающемуся на i и заканчивающемуся на i ( ).
).
Пусть  , тогда по четности/нечетности i (
, тогда по четности/нечетности i ( ) определяем текущий знак “<” или “>”:
) определяем текущий знак “<” или “>”:
Если i -нечетное, то 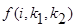 является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра меньше k 2.
Если i -четное, то  является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
является суммой всех количеств i -1-значные волнистых чисел первого типа, которые начинаются на k 1 и у которых последняя цифра больше k 2.
Аналогично, выводится рекуррентное соотношение для волнистых чисел второго типа.
Теорема 1. Количество n -значных волнистых чисел первого типа:

и количество n -значных волнистых чисел второго типа:
 .
.
Составим таблицу некоторых значений f (n, k, k 2)
| k |
|
|
|
|
| |
| 0 | 1 | 0 | 0 | 0 | 0 | |
| 1
 Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...  Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...  Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...  Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов... © cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста. | ||||||