Рассмотрим одномерную периодическую цепочку атомов – одномерный кристалл с одним атомом в элементарной ячейке. Пусть период этой цепочки равен a. Тогда в состоянии равновесия координата n -го атома цепочки xn равна na.
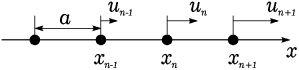
Рис. 1.1. Одномерная цепочка с одним атомом в элементарной ячейке.
Обозначим через un смещение n -го атома из положения равновесия. Будем считать, что атомы взаимодействуют только с ближайшими соседями. Сила, с которой (n +1)–й атом действует на n -й зависит от разности смещений этих двух атомов un +1– un. При небольших смещениях эту силу можно считать пропорциональной разности смещений: Fn , n +1 = γ (un +1– un), где γ – коэффициент пропорциональности. Удобно представить, что атомы связаны друг с другом пружинками с жесткостью γ.
На рис.1.1 пружинка между n -м и n +1 -м атомами растянута, так что она действует на n -й атом в положительном направлении. Растянутая пружинка между n –1-м и n -м атомом действует на n -й атом в отрицательном направлении: Fn , n –1 = – γ (xn – xn –1).
Запишем закон Ньютона для n -го атома цепочки:
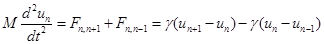 (1).
(1).
Первое слагаемое в правой части – сила, действующая на n -й атом со стороны n +1-го атома, второе – сила, действующая со стороны n –1-го атома.
После упрощения получим:
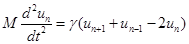 (2).
(2).
Система таких уравнений, записанных для каждого атома, полностью описывает колебания цепочки.
Если рассматривать только длинноволновые колебания, т. е. колебания с длиной волны много большей периода цепочки a, то можно заменить разность un +1– un на (∂ un /∂ x) a, а величину, стоящую в правой части (2) – на γ a 2(∂2 u /∂ x 2). В результате получим волновое уравнение:
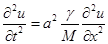 (3).
(3).
Решением которого являются волны u = A exp(ikx – iω t) с линейным законом дисперсии ω = 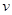 | k | (звуковые волны). Здесь
| k | (звуковые волны). Здесь 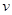 - скорость звука:
- скорость звука: 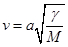 . Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.
. Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.
Будем искать колебания, зависящие от времени по гармоническому закону: un = Cne – iω t (5).
Здесь ω – частота колебаний, одна и та же для всех атомов (такие колебания называются гармоническими). Cn – комплексная амплитуда колебаний n -го атома. Напомним, что колебания описывает вещественная часть уравнения (5), но технически удобно пользоваться комплексным решением.
Такая подстановка – стандартный метод решения линейных систем уравнений с постоянными коэффициентами. В силу линейности уравнений, колебание с произвольной временной зависимостью может быть разложено в интеграл (ряд) Фурье по гармоническим колебаниям.
Из уравнения (2) для амплитуды Cn получаем уравнение:
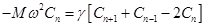 (6).
(6).
Эти уравнения образуют бесконечную систему линейных уравнений. Если применить к цепочке граничные условия Борна-Кармана, то система будет конечной. (Заметим, что условия Борна-Кармана в одномерном случае эквивалентны тому, что цепочка достаточно большой длины L замкнута в кольцо). Тогда, приравняв определитель нулю, можно найти частоты колебаний, а затем, решив систему уравнений для каждой из найденных частот – соответствующие амплитуды.
Но мы поступим иначе. Будем искать решение в виде плоской волны:
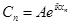 (7).
(7).
Подставив это выражение в (6), получим:
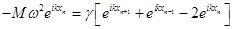 (8)
(8)
Разделим последнее уравнение на exp(ikxn) и воспользуемся тем, что xn +1 = xn + a, xn –1 = xn – a: – M ω 2 = γ (eika + e – ika –2) (9).
Таким образом, подстановка в виде плоской волны оказалась верной: мы избавились от номера атома n и получили уравнение, связывающее ω и k, то есть уравнение, определяющее закон дисперсии волн.
Поскольку: 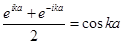 (10), то
(10), то 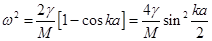 (11).
(11).
Мы получаем закон дисперсии для упругих колебаний одномерной цепочки: 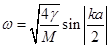 (12).
(12).
Итак, мы пришли к выводу, что смещения атомов при колебании одномерной цепочки описываются плоской гармонической волной:
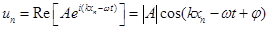 (13).
(13).
Точнее, колебания представляют собой произвольную сумму таких волн. Здесь φ – фаза комплексной амплитуды A: A = | A |exp(iφ). Смещение – вещественная величина, которая описывается вещественной частью комплексной плоской гармонической волны, что явно записано в (13). В дальнейшем, при описании вещественных колебаний комплексной плоской волной, будем для краткости опускать обозначение вещественной части.
Волновой вектор k в плоской волне (13) может, вообще говоря, быть любым. Но вследствие дискретности цепочки (xn может принимать лишь дискретный набор значений na) плоские волны, волновые вектора которых отличаются друг от друга на произвольный вектор обратной решетки 2 π l / a, описывают одно и то же колебание. (Здесь l — любое целое число).
Действительно, так как xn = na, т:
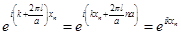 (14).
(14).
Поэтому достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна – π / a < k < π / a. Крайние значения волнового вектора ± π / a соответствуют одному и тому же колебанию с минимальной длиной волны λ = 2 π / k = 2 a. При такой длине волны соседние атомы цепочки движутся в противофазе. Интуитивно ясно, что короче длина волны быть уже не может.
График зависимости ω (k) для одномерной цепочки с одним атомом в примитивной ячейке изображен на рис. 1.2.
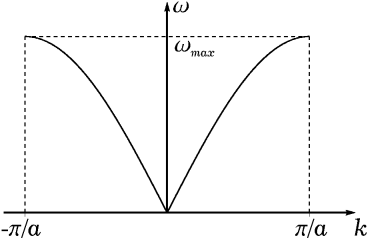 Рис. 1.2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке.
Рис. 1.2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке.
|
Обсудим теперь особенности закона дисперсии (12).
Важным его свойством является то, что частота волн, распространяющихся по цепочке, ограничена частотой 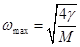 . Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
. Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
Посмотрим на размерность γ. Сила F равна произведению γ на смещение u, поэтому:
 (15).
(15).
Характерная длина, межатомное расстояние a, имеет порядок 1A = 10–8 cм. Характерная энергия – энергия, которую приобретает атом при смещении на расстояние порядка a. Ее можно оценить как энергию химической связи, которая по порядку величины равна 10 эВ. Таким образом:
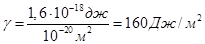 (16).
(16).
В качестве массы для оценки можно подставить величину 10 Mp, где Mp ≈ 1,67· 10–27 кг – масса протона.
Для ωmax получаем:
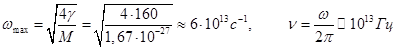 (17).
(17).
Найдем длину волны электромагнитного излучения такой частоты:
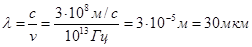 (18).
(18).
Электромагнитные волны с такой длиной принадлежат инфракрасному диапазону.
При ka /2<<1, когда длина волны λ = 2 π / k много больше a, sin(ka /2)≈ ka /2, поэтому:
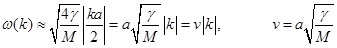 (19).
(19).
Таким образом, длинноволновые колебания – это звуковые волны с линейным законом дисперсии ω = 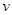 | k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука
| k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука 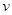 зависит только от макроскопических характеристик цепочки: линейной плотности, M / a, и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения:
зависит только от макроскопических характеристик цепочки: линейной плотности, M / a, и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения:
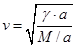 (20).
(20).
Рассмотренные нами колебания одномерной цепочки называют акустическими, поскольку при k → 0 (λ →∞) они соответствуют звуковым волнам.
Ниже мы увидим, что в цепочке с двумя (и более) атомами в элементарной ячейке наряду с акустическими могут распространяться волны другого типа.
При квантовомеханическом описании каждому колебанию соответствует квазичастица с импульсом p = ħ k и энергией 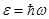 . Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами. Фононы, соответствующие акустическим колебаниям, также называются акустическими.
. Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами. Фононы, соответствующие акустическим колебаниям, также называются акустическими.
Оценим максимальную энергию акустического фонона в одномерной цепочке:
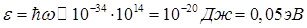 (21)
(21)
Экспериментальные значения ħ ωmax в реальных кристаллах составляют 30 ÷ 40 мэВ.
Эта величина намного меньше большинства характерных электронных энергий (~ 1 эВ) и близка к тепловой энергии при комнатной температуре (kT ≈ 0.025эВ, здесь k – постоянная Больцмана).




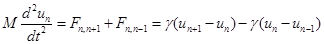 (1).
(1).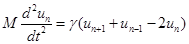 (2).
(2).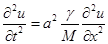 (3).
(3).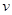 | k | (звуковые волны). Здесь
| k | (звуковые волны). Здесь 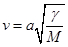 . Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.
. Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.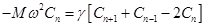 (6).
(6).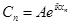 (7).
(7).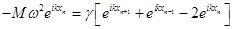 (8)
(8)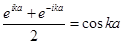 (10), то
(10), то 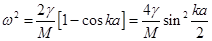 (11).
(11).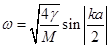 (12).
(12).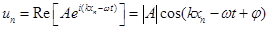 (13).
(13).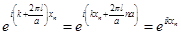 (14).
(14). Рис. 1.2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке.
Рис. 1.2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке.
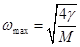 . Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
. Чтобы оценить эту частоту, надо знать порядок величины постоянной γ. (15).
(15).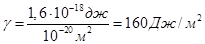 (16).
(16).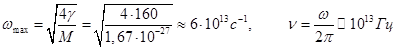 (17).
(17).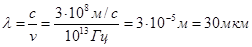 (18).
(18).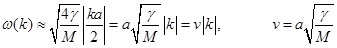 (19).
(19).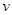 | k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука
| k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука 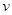 зависит только от макроскопических характеристик цепочки: линейной плотности, M / a, и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения:
зависит только от макроскопических характеристик цепочки: линейной плотности, M / a, и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения: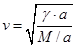 (20).
(20).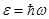 . Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами. Фононы, соответствующие акустическим колебаниям, также называются акустическими.
. Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами. Фононы, соответствующие акустическим колебаниям, также называются акустическими.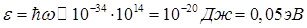 (21)
(21)


