Построение точечного и интервального прогнозов

(7.8)

Если в ходе проверки разрабатываемая модель признана достаточно надёжной, на её основе разрабатывается точечный прогноз. Он получается путём подстановки в модель значений времени t, соответствующих периоду упреждения k: t=n+k. Так, в случае трендовой модели полинома первой степени – линейной модели роста – экстраполяция на k шагов вперёд имеет вид:

.

Для учёта случайных колебаний при прогнозировании рассчитываются доверительные интервалы (интервальный прогноз), зависящие от стандартной ошибки (7.6), горизонта прогнозирования k, длины временного ряда n и уровня значимости прогноза α. В частности, для прогноза (7.8) будущие значения y_n+k с вероятностью (1 – α) попадут в интервал

(7.9)

 

Пример расчета ВР и прогноза по этому ряду

Рассмотрим разработку трендовой модели и получение прогнозных оценок динамики изменения параметра на основе временного ряда, представленного в таблице 7.8.

Таблица 7.8

Исходные данные ВР

t	Параметр
	419,08
	379,8
	410,7

 

Простой анализ данных таблицы 7.8 позволяет сделать вывод о том, что значение параметр y_t монотонно возрастает, т.е. имеется положительный тренд, близкий к линейному, т.к. первый средний прирост примерно одинаков (таблица 7.4). Кроме того среди значений параметра y_t нет аномальных. Все вышеизложенное позволяет сразу перейти к выбору модели ВР. Выбираем в качестве кривой роста линейную модели вида:

и определяем неизвестные значения коэффициентов а₀ и а₁ по методу наименьших квадратов (§ 7.4).

(7.10)

Заполним рабочую таблицу 7.9, где в первой нижней строке таблицы записаны суммы соответствующих граф, во второй – соответствующие средние значения и . Следуя формулам из метода наименьших квадратов, оценим параметры линейной модели роста: а ₀ = 256,36 и а ₁ = 14,32. Таким образом, искомая модель принимает вид:

Последовательно подставляя в (7.10) вместо фактора t его значения от 1 до n =14, заполним остальные графы расчётных уровней таблицы 7.9.

Таблица 7.9

Расчетные данные для ВР

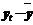
t	yt							Точ. пов
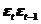
	238,00	-6,5	42,25	-125,76	817,44	270,68	-32,68	-	1067,98	-	-	-
	249,00	-5,5	30,25	-114,76	631,18	285,00	-36,00		1296,00	-3,32	11,02	1176,48
	287,00	-4,5	20,25	-76,76	345,42	299,32	-12,32		151,78	23,68	560,74	443,52
	340,00	-3,5	12,25	-23,76	83,16	313,64	26,36		694,85	38,68	1496,14	-324,76
	342,00	-2,5	6,25	-21,76	54,4	327,96	14,04		197,12	-12,32	151,78	370,09
	373,00	-1,5	2,25	9,24	-13,86	342,28	30,72		943,72	16,68	278,22	431,31
	360,00	-0,5	0,25	-3,76	1,88	356,60	3,40		11,56	-27,32		104,45
	380,00	0,5	0,25	16,24	8,12	370,92	9,08		82,45	5,68	32,26	30,87
	403,00	1,5	2,25	39,24	58,86	385,24	17,76		315,42	8,68	75,34	161,26
	419,10	2,5	6,25	55,34	138,35	399,56	19,54		381,81	1,78	3,16	347,03
	451,00	3,5	12,25	87,24	305,34	413,88	37,12		1377,89	17,58	309,05	725,32
	460,00	4,5	20,25	96,24	433,08	428,20	31,80		1011,24	-5,32	28,30	1180,42
	379,80	5,5	30,25	16,04	88,22	442,52	-62,72		3933,80	-94,52	8934,03	-1994,50
	410,70	6,5	42,25	46,94	305,1 1	456,84	-46,14	-	2128,90	• 16,58	274,89	2893,90
Σ		5092,6		227,50	-0,04	3256,70	5092,64	-0,04		13594,52	-	12901,31	5545,40
ср.	7,5	363,76

 

Для проверки адекватности модели в соответствии с ви­дом формул (7.1), (7.4) и (7.4а) организуем и заполним графы 9 – 13, и строим график (рис. 7.3).

Рис. 7.3. Экспериментальный и теоретический ряды

 

1. Легко убедиться, что математическое ожидание ряда остатков равно нулю, т.е. | | = 0, что следует из суммы 8-ого столбца (-0,04).

2. Проверка случайности ряда остатков по критерию пи­ков дает положительный результат, т.к. р = 7 (9 столбец таблицы 7.9), а критическое число поворотных точек, рассчитанное по формуле (7.3) равно 5. Таким образом, выполняется условие 7>5.

3. При проверке независимости уровней ряда остатков друг от друга значение d = 0,95, вычисленное по формуле (7.4), при уровне значимости α = 0,025 попадает в интервал между d ₁ = 0,920 и d ₂ = 1,060, т.е. в область неопределенности. Поэтому придется воспользоваться формулой (7.4а): r ₁ = 0,41. Сопоставляя это число с табличным значением первого коэффициента ав­токорреляции 0,485, взятым для уровня значимости α = 0,01 и n = 14, увидим, что расчетное значение меньше табличного. Это означает, что с ошибкой в 1% ряд остатков можно считать не­коррелированным, т.е. свойство взаимной независимости уров­ней остаточной компоненты подтверждается.

4. Соответствие ряда остатков нормальному распределению установим с помощью формулы (7.5). Вычислим вари­ационный размах ε _max– ε _max = 99,84 и среднеквадратическое отклонение δ_ε = 32,34. По этим данным рассчитаем критерий R/S =3,09. Для n = 14 и α = 0,05 найдем критическим интервал: [2,92; 4,05]. Вычисленное значение 3,09 попадает между табулированными границами с заданным уровнем вероятности. Значит, закон нормального распределения выполняется, и можно строить до­верительный интервал прогноза.

5. Так как модель оказалась адекватной, оценим ее точность. По формуле (7.7) рассчитаем среднюю относительную ошибку: Е _отн = 7,7%. Такую ошибку можно считать приемлемой, 7,7<15.

6. Экстраполяция уравнения = 256,36 + 14,32 t на шаг впе­ред, т.е. на момент времени n + 1 = 15, дает прогнозное значе­ние параметра, равное 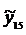= 471,12.

7. Для построения интервального прогноза рассчитаем доверительный интервал (7.9). Примем значение уровня значимости α = 0,3, а значит, доверительную вероятность – 70 %. В этом случае критерий Стьюдента (при v = n –2 = 12) равен t_α,v= 1,083. Вычислив среднеквадратическую ошибку тренда (7.6), с учетом значения t_α,v получим интервальный прогноз (см. рис. 7.3):

где

Таким образом, построенная нами модель является полно­стью адекватной динамике параметра и достаточно надежной для крат­косрочных прогнозов. Поэтому с вероятностью 0,7 (70%) можно утверждать, что при сохранении сложившихся закономерностей развития значения параметра y_t, прогнозируемое на t= 15 с помощью линейной модели роста, попадет в промежуток, обра­зованный нижней и верхней границей доверительного интервала (429,25; 512,99).

 

Адаптивное прогнозирование

Адаптивными методами прогнозирования принято назы­вать такие методы, процесс реализации которых заключается в вычислении последовательных во времени значений прогнози­руемого показателя с учетом степени влияния предшествующих уровней. При краткосрочном прогнозировании наиболее важным является не тенденция развития исследуемого процесса, сложив­шаяся в среднем на всем периоде предыстории, а последние зна­чения этого процесса. Свойство динамичности развития эконо­мического явления здесь преобладает над свойством его инерци­онности. Поэтому при краткосрочном прогнозировании, как правило, более эффективными оказываются адаптивные методы, учитывающие неравноценность уровней временного ряда и бы­стро приспосабливающие свою структуру и параметры к изме­няющимся условиям.

Наиболее распространенным из адаптивных методов является метод Брауна, в котором расчетное значение y_р в момент времени t находится по формуле:

y_p (t) = a ₀ (t – 1 ) + a ₁ (t – 1 )k

где k – количество шагов прогнозирования (обычно k = 1).

Это значение сравнивается с фактическим уровнем, и по­лученная ошибка прогноза

Е (t) = y (t) – y_p(t)

используется для корректировки модели. Корректировка параметров осуществляется по формулам:

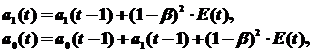
где β – коэффициент дисконтирования данных (уровень значимости), отражающий большую степень доверия к более поздним данным. Его значе­ние должно быть в интервале от 0 до 1. Процесс модификации модели (t = 1, 2,..., n) в зависи­мости от текущих прогнозных качеств обеспечивает ее адап­тацию к новым закономерностям развития. Для прогнозиро­вания используется модель, полученная на последнем шаге (при t = n).

Воспользуемся схемой адаптивного прогнозирования для примера, рассмотрен­ного в §7.7. Начальные оценки параметров получим по первым пяти значениям y_t при помощи метода наименьших квадратов (рис. 7.4).

y5

y4

y3

y2

y1

Рис. 7.4. Получение начальных значений параметров a₀ (0) и a₁ (0)

 

(7.10)

(7.10)

(7.10)

Линейная модель для y ₁ – y ₅ имеет вид: y = 29,9 x + 201,5. Откуда

a ₀(0) = 201,5, a ₁(0) = 29,9.

Возьмём α = 0,8, k = 1 и β = 1 – α = 0,2 и по формулам адаптирования

получим скорректированные значения параметров a ₀(t) и a ₁(t) (таблица 7.10).

Таблица 7.10

Расчет скорректированных значений a₀(t) и a₁(t)

Время	Факт yt	a 0	a 1	Расчет yt	Отклонение Е(t)
		201,50	29,90
		237,74	34,12	231,40	6,600
		249,91	19,49	271,86	-22,860
		286,30	30,75	269,41	17,592
		339,08	45,44	317,05	22,951
		343,70	18,23	384,52	-42,523
		372,56	25,31	361,93	11,073
		361,51	1,08	397,87	-37,870
		379,30	12,22	362,59	17,409
		402,54	19,56	391,52	11,478
	419,1	419,22	17,64	422,10	-3,005
		450,43	26,69	436,86	14,139
		460,68	15,73	477,12	-17,124
	379,8	383,66	-46,10	476,42	-96,615
	410,7	407,77	0,71	337,56	73,139
				408,48

 

Прогнозные оценки по модели расчета y_p (t) получаются путем подстановки в нее значения k = 1, а интервальные – по тем же формулам, что и для кривых роста:

y_p (15) = 407,11 + 0,71 1 = 408,48.

k = 1 (t = 15)

Нижняя граница: 408,48 – 51,26 = 357, 21.

Верхняя граница: 408,48 + 51,26 = 459,75.

Сведем все полученные результаты в таблицу (таблица 7.11) и покажем на графике (рис. 7.5).

Таблица 7.11