Всякое число представляется набором цифр. Способ представления чисел цифрами характеризует систему счисления (код). Наибольшее распространение получили позиционные системы счисления, в которых число, эквивалентное записанной цифре, определяется как значением этой цифры, так и ее положением (позицией) среди других цифр. Основание системы — это число, равное количеству цифр, необходимых для выражения всех чисел в пределах одного разряда. Десятичная (децимальная) система счисления — типичный пример позиционной системы.
Положительное число из i разрядов в позиционной системе с основанием а может быть представлено как
 (1.1)
(1.1)
где х — любая цифра от 0 до а -1; первый член представляет собой старший разряд числа, а последний — младший.
В десятичной системе например, число 573 можно представить как 57310=5×102+7×101+3×100.
В цифровой аппаратуре применяют приборы, которые имеют два рабочих состояния. Здесь наиболее удобными оказались двоичные (бинарные) коды. Существует ряд двоичных кодов, каждый из которых обладает определенными свойствами. В цифровой технике наибольшее применение получил так называемый натуральный двоичный код, в котором i -разрядное число представляется как
 (1.2)
(1.2)
Здесь x может иметь два значения - 0 и 1.
Порядок счета в натуральном двоичном коде совпадает с порядком счета внутри каждого десятичного разряда, что упрощает взаимный перевод чисел десятичного и двоичного кодов. Этот двоичный код называют еще кодом 8421 — по весовым коэффициентам (или короче весам) первых четырех разрядов числа. В дальнейшем при упоминании двоичного кода подразумевается код 8421. В табл. 1.1 приведены десятичные числа от 0 до 15 и их эквиваленты в коде 8421. Из таблицы следует, что для представления десятичных цифр от 0 до 9 (одного десятичного разряда) требуются четыре двоичные цифры, т. е. двоичные числа длиннее эквивалентных десятичных.
Двоичные числа, представленные в таблице, и им подобные характеризуют прямой код. Кроме этого применяются и другие коды, с помощью которых упрощаются арифметические действия. К ним относятся, в частности, обратный и дополнительный коды.
Таблица 1.1
| Код
| Код
| Код
|
| десятичный
|
| десятичный
|
| десятичный
|
|
|
|
|
|
|
|
|
Двоичное число в обратном коде отличается от числа в прямом коде тем, что в каждом разряде имеет 0 вместо 1 и наоборот. Дополнительный код числа образуется из обратного кода добавлением 1 к младшему разряду. Так, десятичному числу - 9 в обратном двоичном коде соответствует число 0110, а в дополнительном - 0111.
Широко применяется двоично-десятичный код, в котором цифры каждого разряда десятичного числа представляются четырехразрядным двоичным числом (тетрадой). Так, число N10=573 в двоично-десятичном коде имеет вил N2-10=0101 0111 0011. Основное достоинство двоично-десятичного кода — в простоте взаимного перевода десятичных и двоичных чисел, так как непосредственное схемное преобразование десятичных чисел в двоичные и наоборот связано с большими аппаратурными затратами. Это важный момент с точки зрения взаимодействия человека с машиной, поскольку в большинстве случаев цифровая информация, подлежащая переработке и преобразованию, задается в десятичном коде и в этом же коде должны быть представлены окончательные результаты. Главный недостаток двоично-десятичного кода — громоздкость и избыточность, так как шесть двоичных комбинаций (от 10102=1010 до 11112 =1510) при этом не используются.
Булева алгебра
Математический аппарат, описывающий действия дискретных устройств, базируется на алгебре логики, или, как ее еще называют по имени автора английского математика Джорджа Буля (1815 - 1864 гг.), булевой алгебре. В практических целях первым применил его американский ученый Клод Шеннон в 1938 г. при исследовании электрических цепей с контактными выключателями.
Булева алгебра оперирует двоичными переменными, которые условно обозначаются как 0 и 1 и подчиняются условиям: x=1, если x¹0, и x=0, если x¹1. В ее основе лежит понятие переключательной, или булевой, функции вида f (x1, x2,..., xn) относительно аргументов x1, x2,..., xn, которая, как и ее аргументы, может принимать только два значения — 0 и 1. Как частный случай, двоичные переменные могут постоянно сохранять одно из значений — 0 либо 1. Логическая функция может быть задана словесно, алгебраическим выражением и таблицей, которая называется таблицей истинности.
Действия над двоичными переменными производятся по правилам логических операций. Между обычной, привычной нам алгеброй и алгеброй логики имеются существенные различия в отношении количества и характера операций, а также законов, которым они подчиняются.
Простейших логических операций три: отрицание (инверсия, операция НЕ), логическое умножение (конъюнкция, операция И) и логическое сложение (дизъюнкция, операция ИЛИ). Более сложные логические преобразования можно свести к указанным операциям.
Операция отрицания выполняется над одной переменной и характеризуется следующими свойствами: функция y =1 при аргументе x=0 и y =0, если x=1. Обозначается отрицание чертой над переменной, с которой производится операция:  (игрек равен не икс). Соответственно
(игрек равен не икс). Соответственно  .
.
Операция логического умножения (конъюнкция) для двух переменных характеризуется табл. 1.2 и обозначается следующим образом: 0×0=0; 0×1=0; 1×0=0; 1×1=1, т. е. нулевое значение хотя бы одного из аргументов обеспечивает нулевой результат операции. Операция может быть распространена на большее число переменных.
Таблица 1.2
Операцию логического сложения (дизъюнкции) определяет табл. 1.3. Обозначают ее таким способом:  , либо
, либо  . Первый способ предпочтителен, так как позволяет отличать логическое сложение от арифметического. Для двух переменных
. Первый способ предпочтителен, так как позволяет отличать логическое сложение от арифметического. Для двух переменных 


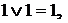 т. е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции.
т. е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции.
Таблица 1.3
Дизъюнкция, как и конъюнкция, может осуществляться с многими переменными.
Совокупность различных значений переменных называют набором. Булева функция n аргументов может иметь до N=2n наборов. Поскольку функция принимает только два значения, общее число булевых функций n аргументов  . Таким образом, функция одного аргумента может иметь четыре значения: у=x; у=
. Таким образом, функция одного аргумента может иметь четыре значения: у=x; у= 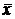 ; у=1 (константа 1); у=0 (константа 0).
; у=1 (константа 1); у=0 (константа 0).
Два аргумента дают 16 значений функции (табл. 1.4).
Таблица 1.4
| Аргументы
| Функция
| Название
функции
|
| x1...0
x2...0
|
|
|
|
|
|
|
|
| y=0
| Константа 0
|
|
|
|
|
| y=x1x2
| Конъюнкция, операция И
|
|
|
|
|
| 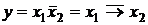
| Запрет по x2
|
|
|
|
|
| y=x1
| Тождественность
(тавтология) x1
|
|
|
|
|
| 
| Запрет по x1
|
|
|
|
|
| y=x2
| Тождественность
(тавтология) x2
|
|
|
|
|
| 
| Исключающее ИЛИ
(сумма по модулю 2)
|
|
|
|
|
| 
| Дизъюнкция, операция ИЛИ
|
|
|
|
|
| 
| Стрелка Пирса
(операция ИЛИ-НЕ)
|
|
|
|
|
| 
| Равнозначность,
эквивалентность
|
|
|
|
|
| 
| Инверсия x2
|
|
|
|
|
| 
| Импликация от x2 к x1
|
|
|
|
|
| y=x1
| Инверсия x1
|
|
|
|
|
| 
| Импликация от x1 к x2
|
|
|
|
|
| 
| Штрих Шеффера
(операция И-НЕ)
|
|
|
|
|
| y=1
| Константа 1
|
Булева алгебра базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с двоичными переменными. Обоснованность выбора этих аксиом подтверждается таблицами истинности для рассмотренных операций. Каждая аксиома представлена в двух видах, что вытекает из принципа дуальности (двойственности) логических операций, согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять логическую 1 на 0, 0 на 1, знак  на ×, а × на
на ×, а × на  .
.
Аксиомы операции отрицания: 
Аксиомы операций конъюнкции и дизъюнкции:
1. 0 × 1 = 1; (а)  ; (б)
; (б)
2. 1 × 0 = 0 × 1 = 0; (а)  ; (б)
; (б)
3. 1 × 1 = 1; (а)  ; (б)
; (б)
Аксиома 16 не имеет аналога в двоичной арифметике, где 1+1=10 (здесь цифры и знаки имеют обычный арифметический смысл).
Законы булевой алгебры вытекают из аксиом и также имеют две формы выражения: для конъюнкции и дизъюнкции. Здесь они приводятся без доказательств. Их правильность легко проверить по таблицам истинности либо путем подстановки 0 и 1 вместо соответствующих значений переменных.
1. Переместительный закон
x1 × x2=x2 × x1; (а)  ; (б)
; (б)
2. Сочетательный закон
x1(x2x3) = (x1x2)x3 = x1x2x3; (а)
 . (б)
. (б)
3. Закон повторения (тавтологии)
x × x = x; (а)  . (б)
. (б)
4. Закон обращения: если x1 = x2, то  .
.
5. Закон двойной инверсии  .
.
6. Закон нулевого множества
x × 0 = 0; (а) 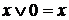 . (б)
. (б)
7. Закон универсального множества
x × 1 = x; (а) 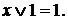 (б)
(б)
8. Закон дополнительности
 ; (а)
; (а)  . (б)
. (б)
9. Распределительный закон
 (а)
(а)
 (б)
(б)
10. Закон поглощения
 (а)
(а)  (б)
(б)
11. Закон склеивания
 (а)
(а)  (б)
(б)
12. Закон инверсии (закон Де Моргана)
 (а)
(а)  (б)
(б)
или после инвертирования левых и правых частей
 (в)
(в)  (г)
(г)



 (1.1)
(1.1) (1.2)
(1.2) (игрек равен не икс). Соответственно
(игрек равен не икс). Соответственно  .
. , либо
, либо  . Первый способ предпочтителен, так как позволяет отличать логическое сложение от арифметического. Для двух переменных
. Первый способ предпочтителен, так как позволяет отличать логическое сложение от арифметического. Для двух переменных 


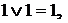 т. е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции.
т. е. равенство хотя бы одного аргумента логической единице определяет единичное значение всей функции. . Таким образом, функция одного аргумента может иметь четыре значения: у=x; у=
. Таким образом, функция одного аргумента может иметь четыре значения: у=x; у= 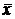 ; у=1 (константа 1); у=0 (константа 0).
; у=1 (константа 1); у=0 (константа 0).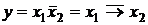









 на ×, а × на
на ×, а × на 
 ; (б)
; (б) ; (б)
; (б) ; (б)
; (б) ; (б)
; (б) . (б)
. (б) . (б)
. (б) .
. .
.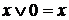 . (б)
. (б)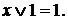 (б)
(б) ; (а)
; (а)  . (б)
. (б) (а)
(а) (б)
(б) (а)
(а)  (б)
(б) (а)
(а)  (б)
(б) (а)
(а)  (б)
(б) (в)
(в)  (г)
(г)


