

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Задание 1. Вычислить криволинейные интегралы:
1.  L – ломаная АВС, где А(1;2), В(1;5), С(3;5).
L – ломаная АВС, где А(1;2), В(1;5), С(3;5).
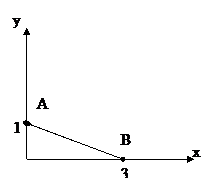
2.  , где L – контур Δ ОАВ: О(0;0), А(2;0), В(4;5).
, где L – контур Δ ОАВ: О(0;0), А(2;0), В(4;5).
3.  , где L – дуга параболы x = y2 от т. А(1;1) до В(25;5).
, где L – дуга параболы x = y2 от т. А(1;1) до В(25;5).
4.  где L – контур Δ АВС: А(1;0), В(1;1), С(0;1).
где L – контур Δ АВС: А(1;0), В(1;1), С(0;1).
5.  .
.
6. 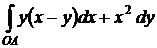 по линии y = 2 x2 от О(0;0) до А(1;2).
по линии y = 2 x2 от О(0;0) до А(1;2).
7.  по линии y2 = 4 x от О(0;0) до А(1;2).
по линии y2 = 4 x от О(0;0) до А(1;2).
8.  вдоль параболы
вдоль параболы  от начала координат до точки А(1;2).
от начала координат до точки А(1;2).
9.  , где L –отрезок прямой от точки А (1;2) до В(2;4).
, где L –отрезок прямой от точки А (1;2) до В(2;4).
10.  по контуру фигуры, ограниченной линиями у = х2, у = 9.
по контуру фигуры, ограниченной линиями у = х2, у = 9.
11.  , где L – дуга кривой у = х2 + 3х, –
, где L – дуга кривой у = х2 + 3х, –  .
.
12.  вдоль параболы
вдоль параболы  от начала координат до точки А(1;2).
от начала координат до точки А(1;2).
13.  , где L – отрезок ОА, О(0;0), А(1;2).
, где L – отрезок ОА, О(0;0), А(1;2).
14.  , где L – дуга кривой х = t; y =
, где L – дуга кривой х = t; y = 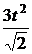 ; z =
; z =  , где
, где  .
.
15.  по окружности
по окружности 
 ;
;  .
.
16.  , где L – окружность
, где L – окружность  .
.
17.  .
.
18.  , где L – контур треугольника АВС: А(1;1), В (2;2), С (1;3).
, где L – контур треугольника АВС: А(1;1), В (2;2), С (1;3).
19.  , где L:
, где L:  от т. М (1;1) до т. N (2;8).
от т. М (1;1) до т. N (2;8).
20.  , где L – прямоугольник:
, где L – прямоугольник:  .
.
21. 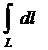 , где L:
, где L:  и
и  .
.
22. 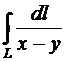 , где L – отрезок прямой
, где L – отрезок прямой 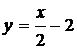 между точками А(0;-2) и В(4;0).
между точками А(0;-2) и В(4;0).
23.  , где L – четверть эллипса
, где L – четверть эллипса  , лежащая в первой четверти.
, лежащая в первой четверти.
24.  , где L – окружность
, где L – окружность  .
.
25.  .
.
26.  , где L:
, где L:  и
и  .
.
27.  , где L:
, где L:  и
и  .
.
28.  , где L – эллипс
, где L – эллипс  .
.
29.  , где L – окружность с центром в начале координат.
, где L – окружность с центром в начале координат.
30.  , где L – дуга кривой
, где L – дуга кривой  от точки А (2;2) до точки В(4;4).
от точки А (2;2) до точки В(4;4).
Задание 2. Проверить, является ли заданное выражение дифференциалом некоторой функции 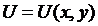 и в случае положительного ответа найти
и в случае положительного ответа найти  с помощью криволинейного интеграла.
с помощью криволинейного интеграла.
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7. 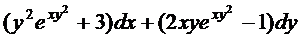 ;
;
8. 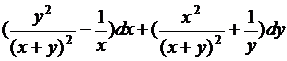 ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12. 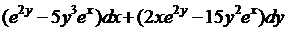 ;
;
13.  ;
;
14.  ;
;
15.  ;
;
16.  ;
;
17.  ;
;
18.  ;
;
19.  ;
;
20.  ;
;
21. 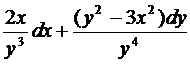 ;
;
22.  ;
;
23.  ;
;
24.  ;
;
25.  ;
;
26. 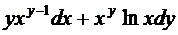 ;
;
27.  ;
;
28. 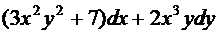 ;
;
29.  ;
;
30.  .
.
Элементы теории поля.
Задание 3. Даны векторное поле  и плоскость
и плоскость 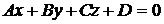 (p), которая совместно с координатными плоскостями образует пирамиду V. Пусть
(p), которая совместно с координатными плоскостями образует пирамиду V. Пусть  - основание пирамиды, принадлежащее плоскости (p);
- основание пирамиды, принадлежащее плоскости (p);  - контур, ограничивающий
- контур, ограничивающий  ;
;  - нормаль к
- нормаль к  , направленная вне пирамиды V.
, направленная вне пирамиды V.
Требуется вычислить:
|
|
1. Поток векторного поля  через поверхность
через поверхность  в направлении нормали
в направлении нормали  .
.
2. Циркуляцию векторного поля  по замкнутому контуру
по замкнутому контуру  , применив теорему Стокса.
, применив теорему Стокса.
3. Поток векторного поля  через полную поверхность пирамиды, применив теорему Остроградского.
через полную поверхность пирамиды, применив теорему Остроградского.
1.  ; (p):
; (p):  .
.
2.  ; (p):
; (p): 
3.  ; (p):
; (p): 
4.  ; (p):
; (p): 
5.  ; (p):
; (p): 
6.  ; (p):
; (p): 
7.  ; (p):
; (p): 
8.  ; (p):
; (p): 
9.  ; (p):
; (p): 
10.  ;(p):
;(p): 
11.  ; (p):
; (p): 
12.  ; (p):
; (p): 
13.  ; (p):
; (p): 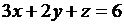
14.  ; (p):
; (p): 
15. 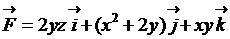 ; (p):
; (p): 
16.  ; (p):
; (p): 
17.  ; (p):
; (p): 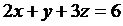
18.  ; (p):
; (p): 
19.  ; (p):
; (p): 
20.  ; (p):
; (p): 
21.  ; (p):
; (p): 
22.  ; (p):
; (p): 
23.  ; (p):
; (p): 
24.  ; (p):
; (p): 
25.  ; (p):
; (p): 
26.  ; (p):
; (p): 
27.  ; (p):
; (p): 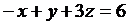
28.  ; (p):
; (p): 
29.  ; (p):
; (p): 
30. 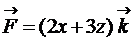 ; (p):
; (p): 
Задание 4. Даны функция  и вектор
и вектор  .
.
Требуется:
1) найти направление наибольшего возрастания функции в точке М  и скорость возрастания функции в этом направлении;
и скорость возрастания функции в этом направлении;
2) найти  ;
;
3) найти  .
.
1.  ;
; 
2.  ;
; 
3.  ;
; 
4. 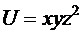 ;
; 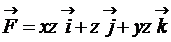
5. 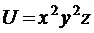 ;
; 
6.  ;
; 
7.  ;
; 
8.  ;
; 
9.  ;
; 
10.  ;
; 
11.  ;
; 
12. 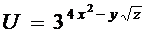 ;
; 
13.  ;
; 
14.  ;
; 
15.  ;
; 
16.  ;
; 
17.  ;
; 
18.  ;
; 
19.  ;
; 
20.  ;
; 
21.  ;
; 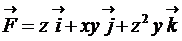

22.  ;
; 
23.  ;
; 
24.  ;
; 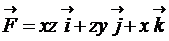
25.  ;
; 
26.  ;
; 
27.  ;
; 
28.  ;
; 
29.  ;
; 
30.  ;
; 
Задание 5. Выяснить, имеет ли данное векторное поле потенциал и найти его, если он существует.
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. 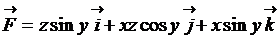 ;
;
6.  ;
; 
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
; 
12. 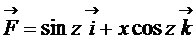 ;
;
13.  ;
;
14.  ;
;
15. 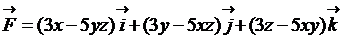 ;
;
16.  ;
;
17.  ;
;
18.  ;
;
19.  ;
;
20.  ;
;
21.  ;
;
22.  ;
;
23.  ;
;
24. 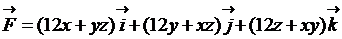 ;
;
25.  ;
;
26. 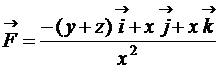 ;
;
27.  ;
;
28.  ;
;
29.  ;
;
30.  .
.
Образец выполнения контрольной работы №9
Задание 1
1. вычислить криволинейный интеграл.
 , где L- отрезок прямой от точки А(0;1) до В(1;3)
, где L- отрезок прямой от точки А(0;1) до В(1;3)
Решение: данный интеграл криволинейный интеграл II-го разряда.
а) найдем уравнение прямой АВ по формуле: 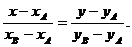
Получим: 
б) применим формулу 
тогда, с учетом того, что  , если
, если 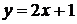 , и
, и 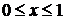 , получим:
, получим:
 ответ 3,5
ответ 3,5
Задание 2
Вычислить 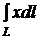 , если L:
, если L:  и
и 
Решение: данный интеграл есть криволинейный интеграл I разряда.
Используем формулу: 

Тогда 
 =
=
= 
 =
=
= 
 =
= 

 =
=  =
=
= 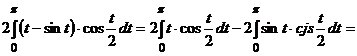




 =
=
=  =
=
=2  -4
-4 
 =
=
= 
Таким образом, 
Ответ:  .
.
Задание 3
Вычислить

Решение:
а) проверим условие 


условие  выполняется значит, интеграл не зависит от пути интегрирования.
выполняется значит, интеграл не зависит от пути интегрирования.
б)
в качестве пути интегрирования выберем ломанную АОВ, звенья которой параллельны координатным осям:
АО  ОУ; управления АО: х=0
ОУ; управления АО: х=0  dx=0
dx=0
ОВ  ОХ; управления ОВ: у=0
ОХ; управления ОВ: у=0  dy=0
dy=0
в)

|
|
Ответ:  .
.
Задание 4
Вычислить  , где L:
, где L: 
Решение:
а) проверим условие (*): 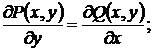


Условие (*) не выполняется.
Замечание: если условие (*) выполняется, то 
б) Вычислим интеграл по формуле Грина:
 ,
,
где D-область, ограниченная контуром L.
У нас,  =
=
= 
Ответ: 
Задание 2. Проверить является ли заданное выражение дифференциалом некоторой функции  и, в случае положительного ответа, найти U с помощью криволинейного интеграла:
и, в случае положительного ответа, найти U с помощью криволинейного интеграла:

Решение:
Выражение  является полным дифференциалом, если верно:
является полным дифференциалом, если верно: 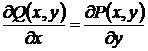 (*)
(*)
Проверим:
а) 
б) 
 в данное выражение является полным дифференциалом некоторой функции U. Найдем ее, используя формулу:
в данное выражение является полным дифференциалом некоторой функции U. Найдем ее, используя формулу:

где  точка из пересечения областей определения функций
точка из пересечения областей определения функций 

= 
= 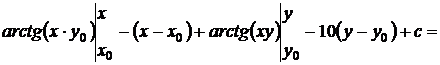
= 
= 
Т.о, 
Элементы теории поля.
Задание 3.
Дано:
Векторное поле: 
Плоскость р: 
Пирамида  образованная плоскостью р и координатными плоскостями
образованная плоскостью р и координатными плоскостями
 - основание пирамиды, принадлежащее плоскости р;
- основание пирамиды, принадлежащее плоскости р;
 - контур, ограничивающий
- контур, ограничивающий  ;
;
 - нормаль к
- нормаль к  , направленная вне пирамиды V.
, направленная вне пирамиды V.
Вычислить:
1). Поток в.п.  через поверхность
через поверхность  в направлении нормали
в направлении нормали 
2). Циркуляцию в.п.  по замкнутому контуру
по замкнутому контуру  , применив теорему Стокса.
, применив теорему Стокса.
3). Поток в.п.  через полную поверхность пирамиды, применив теорему Остроградского.
через полную поверхность пирамиды, применив теорему Остроградского.
Решение:
Сделаем чертеж:









где  -проекция
-проекция  на
на  ;
;
 - координаты нормали к поверхности
- координаты нормали к поверхности  .
.
а) 
= 
знак выбираем исходя из того, что  , т.к
, т.к 
Т.о, 

б)

в) 
г) 
= 
д) 

= 
= 
Ответ: 
2. Теорема Стокса:

= 
где б - поверхность, «натянутая» на контур L
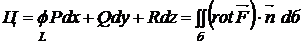 - вычисление циркуляции по формуле Стокса.
- вычисление циркуляции по формуле Стокса.
а) 

б) 
в) 
Ответ: 
3. Теорема Остроградского:
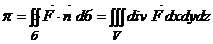
а) 

б) 
Ответ: 
Задание 4
Дано:
 - функция
- функция
 -векторное поле.
-векторное поле.
Найти:
1) направление наибольшего возрастания функции в точке М (х, у,z) и скорость возрастания функции в этом направлении;
2)  ;
;
3) 
Решение:
1) задание можно сформулировать так: найти  и
и 


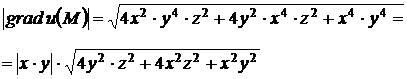
2) 
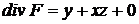



Задание 5. Выяснить, имеет ли данное векторное поле потенциал и найти его, если он существует.

Решение: Векторное поле является потенциальным, если
 . Проверим.
. Проверим.

Поле является потенциальным. Найдем его потенциал, используя формулу:
|
|
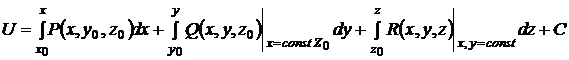
где  -произвольная точка из пересечения областей определения функций
-произвольная точка из пересечения областей определения функций 



где 
Таким образом, 
Проверка: U- потенциал поля U, то должно быть верно: 
(См. задание). Вывод: потенциал вычислен, верно.
Ответ: 
Контрольная работа №10.
Теория вероятностей.
Задание 1. В партии из № изделий n изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад m изделий k изделий являются дефектными.
| Вариант | № | n | m | k | Вариант | № | n | m | k |
Задание 2. В магазине выставлены для продажи n изделий, среди которых k изделий некачественные. Какова вероятность того, что взятые случайным образом m изделий будут некачественными.
| Вариант | n | k | m | Вариант | n | k | m |
Задание 3. На сборочное предприятие поступили комплектующие изделия с трех заводов в количестве:  с первого завода,
с первого завода,  со второго завода,
со второго завода,  с третьего. Вероятность качественного изготовления изделий на первом заводе
с третьего. Вероятность качественного изготовления изделий на первом заводе  , на втором
, на втором  , на третьем
, на третьем  . Какова вероятность того, что взятое случайным образом изделие будет качественным?
. Какова вероятность того, что взятое случайным образом изделие будет качественным?
|
|
| Вариант | 
| 
| 
| 
| 
| 
| Вариант | 
| 
| 
| 
| 
| 
|
| 0,9 | 0,8 | 0,7 | 0,9 | 0,8 | 0,7 | ||||||||
| 0,8 | 0,7 | 0,7 | 0,8 | 0,7 | 0,9 | ||||||||
| 0,9 | 0,7 | 0,9 | 0,9 | 0,8 | 0,8 | ||||||||
| 0,7 | 0,9 | 0,8 | 0,8 | 0,6 | 0,7 | ||||||||
| 0,9 | 0,8 | 0,6 | 0,9 | 0,8 | 0,7 | ||||||||
| 0,8 | 0,8 | 0,9 | 0,9 | 0,7 | 0,8 | ||||||||
| 0,8 | 0,9 | 0,8 | 0,9 | 0,8 | 0,9 | ||||||||
| 0,7 | 0,8 | 0,9 | 0,9 | 0,7 | 0,7 | ||||||||
| 0,9 | 0,8 | 0,9 | 0,8 | 0,9 | 0,8 | ||||||||
| 0,8 | 0,7 | 0,8 | 0,8 | 0,8 | 0,9 | ||||||||
| 0,9 | 0,9 | 0,8 | 0,9 | 0,8 | 0,6 | ||||||||
| 0,8 | 0,9 | 0,8 | 0,8 | 0,7 | 0,8 | ||||||||
| 0,8 | 0,9 | 0,7 | 0,8 | 0,9 | 0,8 | ||||||||
| 0,9 | 0,7 | 0,7 | 0,9 | 0,8 | 0,9 | ||||||||
| 0,8 | 0,9 | 0,9 | 0,7 | 0,9 | 0,7 |
Задание 4. Дано распределение дискретной случайной величины X. Найти
математическое ожидание, дисперсию и среднее квадратичное отклонение.
| Вариант | Числовые значения | Вариант | Числовые значения | ||||||||
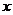
| -5 | 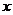
| |||||||||
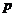
| 0,4 | 0,3 | 0,1 | 0,2 | 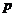
| 0,4 | 0,3 | 0,3 | |||
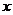
| 0,2 | 0,5 | 0,6 | 0,8 | 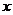
| ||||||
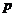
| 0,1 | 0,5 | 0,2 | 0,2 | 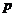
| 0,3 | 0,1 | 0,1 | 0,5 | ||
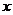
| -6 | -2 | 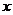
| ||||||||
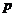
| 0,1 | 0,3 | 0,4 | 0,2 | 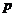
| 0,3 | 0,2 | 0,1 | 0,4 | ||
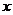
| 0,2 | 0,5 | 0,6 | 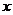
| |||||||
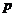
| 0,5 | 0,4 | 0,1 | 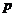
| 0,4 | 0,2 | 0,1 | 0,3 | |||
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!