Линейные образы на плоскости

Введение

Назначение опорного конспекта – служить ключом для самостоятельной работы.

Заочник учится самостоятельно!(в основном!) Поэтому количество часов, отведенных на самостоятельную работу заочников очень велико, и информацию придётся брать из разных источников, в основном из интернета. Однако, обратившись к интернету, вы сразу обнаружите, что эти источники информации изобилуют деталями, предостережениями, примечаниями, описаниями особых случаев, и легко можно отвлечься и заблудиться в деталях. Кроме этого, сильно мешает и разнобой в обозначениях и названиях.

Много отличной переводной литературы по математике, но за рубежом своя терминологическая традиция, и с помощью интернета источники информации постоянно испытывают «перекрёстное опыление», что затуманивает картину.

Поэтому в данном опорном конспекте акцент сделан на показ общей картины наиболее кратким способом. Подробности, по мере надобности, возьмёте из интернета.

Опорный конспект поможет сориентироваться при первом чтении, чтобы студент мог быстро уловить суть предмета.

Главный совет: когда затрудняетесь понять, что означает близкие по звучанию термины, сначала принимайте на веру предположение, что они означают одно и то же. Ньюансы проявятся потом.

На первом курсе бакалавры втуза изучают по математике такие разделы:

 

1. Аналитическую геометрию,

2. линейную алгебру,

3. математический анализ.

 

Для усвоения этих (и дальнейших!) разделов математики следует использовать следующие идеи.

А. Идея изоморфизма. Если каждому элементу одного множества можно взаимно однозначно поставить в соответствие элемент другого множества, причем операции на первом множестве можно заменить эквивалентными операциями на втором, то мы спокойно можем рассматривать действия на первом множестве и переносить их результаты на элементы второго. Можно делать и наоборот, когда это удобнее.

Пример. Множество вещественных чисел и числовая ось. Каждому отрезку соответствует число, а каждому числу – отрезок. Поэтому при решении задач мы постоянно перескакиваем от рассмотрения на числовой оси к рассмотрению в виде десятичных дробей, и наоборот.

Б. Всякая теорема вначале была предположением, которое удалось доказать.

Пример. Теорема Пифагора.

В. Замкнутое относительно операций множество. Это такое множество, что операции, выполняемые на нём, снова порождают элементы этого же множества, то есть элементы, обладающие такими же свойствами. Это позволяет знания, полученные на отдельных примерах, переносить на все элементы множества. Пример. Линейное пространство – множество, замкнутое относительно операции «линейная комбинация», которая порождает всё указанное пространство, используя только п базисных векторов.

Г. Теория представлений. Она гласит, что в математике 90% успеха зависит от того, насколько удачное представление мы выберем для задачи.

Пример. Разнообразные дополнительные построения в геометрии. Если мы для доказательства теоремы Пифагора нарисуем «пифагоровы штаны», то доказательство будет сложнее, чем в случае, когда мы нарисуем трапецию.

Д. Любое условие любой математической задачи – это ограничение, наложенное на

переменные. Требуется найти те значения переменных, которые удовлетворяют ограничениям.

Основная идея аналитической геометрии – исследовать геометрические образы с помощью уравнений, введя систему координат и записав для каждой фигуры соответствующие уравнения или неравенства. При этом геометрическую интерпретацию решениям систем уравнений дают пересечения – как фигур между собой, так и с координатными плоскостями и осями.

Линейная алгебра выросла из факта, что математические закономерности, которые легко интерпретировать геометрически, можно перенести на системы уравнений со многими неизвестными, если ввести понятие N-мерного пространства.

Мостиком, соединяющим линейную алгебру и аналитическую геометрию, являются понятия линейной комбинации и линейной зависимости.

Математический анализ вырос из потребности делать астрономические и технические расчёты с неограниченной точностью, но так, чтобы избежать «проклятия вычислений»! Противоречивость этой задачи служит главной причиной «непонятной запутанности» матанализа и теоретической механики.

В дополнение к известным из элементарной математики действиям в матанализе вводится ещё одно действие – операция предельного перехода. Она позволяет доказывать теоремы, верные для любой точности расчётов, какая потребуется нам в будущем.

Очень важными понятиями в матанализе являются понятия переменной величины и непрерывной функции.

Переменная величина – это не число! Основное свойство числа – занимать твёрдо установленное место в ряду других чисел. Переменная величина может принимать разные значения из допустимого диапазона.

Вы найдёте множество определений понятия функции. Мы будем пользоваться в основном старомодным определением, что функция – это зависимая переменная.

Пример. Самолет выполняет фигуры высшего пилотажа. Лётчик по своей прихоти направляет его, то вверх, то вниз. Высота – независимая переменная. А давление воздуха за бортом? Оно зависит от высоты. Оно такое, каким быть ему предназначено законом природы.

Слово функция можно перевести как «назначение». Функционер – человек, который назначен и функционирует, то есть делает то, что ему назначено делать.

Непрерывная функция – такая, что неограниченно сближающимся значениям аргумента соответствуют неограниченно сближающиеся значения функции.

Понятие непрерывной функции – изобретение, позволяющее развивать математические теории, пригодные для любой точности измерений, которую позволяет технический прогресс. И причём в докомпьютерную эпоху.

Из матанализа выросла теория дифференциальных уравнений – вершина классической математики и физики вплоть до начала ХХ века. Схема проста: наблюдая изменяющиеся явления природы, записываем ограничения, которые накладывает природа на скорости изменений, в форме уравнений. Дифференциальных уравнений. Затем, решая уравнения, находим функции, описывающие явления природы в численной форме. Эти функции, в теоретической механике, например, так и величаются: «закон движения».

 

Синусы! Косинусы! Тангенсы! Котангенсы!

 

 

Линейная алгебра и аналитическая геометрия.

Решение систем уравнений

Часто практические потребности заставляют нас решать системы линейных уравнений, состоящие из числа, гораздо большего, чем три уравнения. Например, в экономике. Однако геометрическое представление полезно и в таком случае, так как основные свойства систем, пояснённые геометрически, часто весьма нехитрым способом переносятся и на случай N уравнений.

Формулы (6) и (8) задают систему линейных уравнений 2-го порядка (2 неизвестных)

Формула (12) задаёт систему линейных уравнений 3-го порядка (3 неизвестных).

 

Решения системы – набор чисел, подставив которые вместо неизвестных получаем тождества сразу для всех уравнений.

 

Линейные системы чаще всего решают методом последовательного исключения неизвестных. Например, из формул (6) получим:

.

Подставив это выражение во 2-е уравнение системы (6), получим одно уравнение с одним неизвестным, которое решаем как обычно.

 

Таким же манером решаем и любую систему N уравнений с N неизвестными.

В итоге неизвестные выразятся через матрицу известных коэффициентов 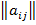и вектор –столбец известных свободных членов .

Когда хотя бы один из свободных членов отличен от нуля, система называется неоднородной, когда все они равны нулю – она однородная.

Решение называется тривиальным, когда все «иксы» равны нулю. И напротив, нетривиальным, если хотя бы один из них отличен от нуля.

Когда переменных много, решение получается громоздким. Чтобы не повторять каждый раз одни и те же выкладки, существуют правила Крамера. Они используют понятие определителя (детерминанта).

Детерминант – это число, получаемое из квадратной (N×N) матрицы по определённому алгоритму. Определитель существует для матрицы любого порядка. Для начала приведём формулы для определителей 2-го и 3-го порядков.

Определитель матрицы (7) имеет вид: . (14)

 

Определитель для матрицы системы (12) имеет вид:

 

(15)

 

В определителе 5-го порядка таких слагаемых будет уже 120. Поэтому определители порядка выше 3-го в общем виде никогда на выписывают.

Как рассчитать определитель любого порядка?

На практике достаточно знать, как свести определители высокого порядка к определителям 2-го и 3-го порядка. Ответ на этот вопрос даёт теорема Лапласа о дополнительных минорах (адъюнктах).

Минор – это «младший» определитель. Он образуется из исходного определителя вычеркиванием какой-то строки и какого-то столбца. Всего у определителя N порядка N² миноров.

Матрицу обычно записывают как таблицу в круглых скобках, а определитель – как таблицу в прямых скобках.

Учитывая это, запишем правила Крамера для системы (12):

 

(*)

 

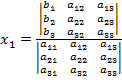
В знаменателе стоит определитель из элементов матрицы, называемый определителем системы.

Ввиду важности этих правил обозначим их звездочкой.

Напоминаем, что каждый определитель – это число, рассчитанное по определённому алгоритму. Поэтому в формуле (*) и числители, и знаменатели – числа.

Теорема Лапласа о дополнительных минорах позволяет последовательно, шаг за шагом, понижать порядок вычисляемого определителя разложением его по строке или по столбцу. В итоге определитель высокого порядка выражается через определители порядка не более 3-его, затем используются формулы (14) и (15).

 

Поясним примером с определителем 4-го порядка.

 

 

Здесь для разложения берём первую строку. Для дополнительным минором будет определитель 3-го порядка, полученный вычеркиванием строки и столбца, в котором стоит . Помножаем этот определитель на (-1) ^i+j , то есть, в данном случае просто на .

Дополнительный минор для получается аналогично, но помножать его надо на .

И далее из одного определителя 4-го порядка получаем 4 определителя 3-го порядка.

Ясно, что решение систем выше 3-го порядка вручную весьма трудоёмкое занятие.

Однако решение систем уравнений 4-го,5-го, 6-го и более высоких порядков давным- давно запрограммировано и совершается на компьютерах за доли секунды.

Подсчёт определителей высокого порядка тоже имеет большое практическое значение. Ибо чтобы неоднородная система имела решение, необходимо, чтобы её определитель был не равен нулю. Подсчет определителя любого порядка меньше 20 занимает на компьютере доли секунды.

Лауреат Нобелевской премии по экономике Василий Васильевич Леонтьев, составляя экономически модели для подъёма экономики Дании, Норвегии и Японии после 2-й мировой войны, обходился моделями из примерно 30 линейных уравнений. В наши дни такие модели легко просчитываются на любом персональном компьютере.

Теперь рассмотрим однородные системы. Начнём с системы 2-го порядка. Две прямые, ей соответствующие, пересекаются в точке{0,0}или же совпадают. Далее перейдём к системе 3-го порядка. Три плоскости пересекаются в точке {0,0,0}, или все три совпадают, проходя через {0,0,0}, или две совпадают, а третья их пересекает, однако они всё равно проходят через точку {0,0,0}. Однако, когда наличествует полное или частичное совпадение, всем трём уравнениям одновременно удовлетворяет не единственная точка {0,0,0}, а все точки прямой проходящей через эту точку, или даже все точки плоскости, которая образовалась после слияния трёх плоскостей.

В общем случае об однородных системах линейных уравнений доказана теорема:

Кривые 2-го порядка

(18)

 

(18) – это общее алгебраическое уравнение 2-го порядка.

Часто его записывают и в виде (19):

 

(19)

Все свойства кривых (18) и (19) определяются наборами коэффициентов, которые одни авторы предпочитают группировать в виде матрицы, как слева или как справа, это дело вкуса.

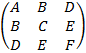(18а) (19а)

 

 

Важно! При переходе в другую декартову систему координат с помощью поворота или сдвига тип кривой не изменяется, но входящие в матрицу коэффициенты становятся другими.

Поворотом осей можно сделать так, чтобы в новой системе координат избавиться от слагаемого , подобрав поворот так, чтобы новый коэффициент В стал равен нулю. Более того, систему координат можно взять и такую, чтобы в новом уравнении исчезли бы слагаемые с первыми степенями х и у.

Для этого начало отсчета следует перенести в новую точку. Куда?

Но для начала рассмотрим:

 

 

Поверхности 2-го порядка

 

(24)

Или, что то же самое,

 

(25)

(24) и (25) – это тоже общее алгебраическое уравнение 2-го порядка, как и (18) и (19).

 

 

Но уже для трех переменных, а, значит, и определяет фигуры для 3-х мерного пространства. Оно, по аналогии с уравнением плоскости, задаёт поверхности в пространстве. Поверхности 2-го порядка уже сложнее и разнообразнее, чем плоскости. Все возможные плоскости интерпретируются как полученные из одной-единственной путём сдвигом и поворотов. С поверхностями 2-го порядка дела обстоят посложнее, но, всё-таки, это самые простые(в аналитическом смысле) представители искривлённых геометрических образов.

Для поверхностей 2-го порядка тоже существуют инварианты. Они задаются следующими формулами.

 

= (26)

 

= + (27)

 

(28) (29)

По инвариантам можно определить тип поверхности и привести уравнение к самому общепринятому (каноническому) виду.

По сравнению с двумерным случаем, разнообразие несколько увеличивается, и помимо ожидаемых эллипсоида, гиперболоида и параболоида появляются и такие фигуры как гиперболический параболоид, конус и различные цилиндры.

Как производить анализ таких фигур, можно найти в справочнике [Корн, Корн]. На данном этапе вам важно лишь усвоить принцип. В настоящее время красивый график для любого уравнения легко можно построить с помощью какой-либо компьютерной математической системы, например, Maple, Mathematica, MatLab. Эта лёгкость заметно снижает практическую ценность теории инвариантов для 2-х и 3-х мерных пространств.

 

 

Введение в матанализ

Важнейшие понятия

1. Число. Оно появляется в результате измерения. (Счёт тоже можно называть измерением.)

Служит для сравнения. А сравнение необходимо для того, чтобы сделать выбор, оказать предпочтение. Наша возможность что-либо аргументировано решать – весьма ограничена, пока мы не переходим к рассмотрению чисел. Числа можно изображать точками на числовой прямой. Длина отрезка, отложенного от нуля вправо, изображает положительное число, а отложенного влево от нуля – отрицательное число. Когда нам удобно, мы вместо чисел рассматриваем отрезки. От рассмотрения отрезков мы с легкостью перейдём к рассмотрению чисел, если так удобнее.

2. Переменная величина. Она принимает численные значения, но это не число! Назначение числа – твёрдо стоять на своём месте в ряду других чисел, полученных той же самой процедурой измерения. А переменная может принимать различные значения из диапазона.

3. Независимая переменная. Насекомое, которое летает в банке, каждый момент времени имеет произвольные координаты, ни от кого не зависимые.

4. Функция. Это величина, значения которой зависят от других величин. Она принимает те значения, которые ей назначено принимать. Функция в физике, химии, биологии – математическое описание закона природы. Закон одно разрешает, иное – запрещает.

Пример. Камень падает в колодец. Глубина падения, в зависимости от времени, меняется по закону , и никак иначе.

Функции задаются: графически, аналитически, таблично.

Аналитически – значит знаем алгоритм, как вычислить значение функции для данного аргумента (Аргумент – та независимая переменная, от которой как раз и зависит функция.)

5. Последовательность. Это функция натурального аргумента. С помощью последовательностей вычисляют функции внутри калькулятора, и не только.

Примеры .

6. Предел последовательности. Это число а, такое, что начиная с некоторого n, все члены последовательности попадают в сколь угодно малую окрестность этого числа а.

7. Неперывность функции. Функция f(x) называется непрерывной в точке x=a, если . Функция f(x) называется непрерывной на отрезке, если она непрерывна в каждой точке х, принадлежащей отрезку.

8. Бесконечно малые функции. Функция f(x) называется бесконечно малой в окрестности точки x=a, если . Функция f(x) называется бесконечно малой более высокого порядка малости, чем функция g(x), если

Примеры. Функция f(x)=х³ при и функция g(x)=х². .

Производная

Следующим важнейшим понятием является понятие производной функции.

Три смысла у производной: физический, геометрический, аналитический.

Физический смысл: если некая величина меняется со временем, то у этого изменения есть скорость.

Геометрически смысл: если мы построим график зависимости величины (например, как путь зависит от времени), и построим касательную в любой точке, то тангенс наклона касательной и будет производная.

Аналитический смысл: . Эта формула на графике соответствует процессу превращения хорды в касательную.

 

Все три смысла равносильны. Они дают свободу выбора при интерпретациях подходов к решению и толкованиях результатов.

Исходная функция, для которой мы вычисляем производную функцию, называется первообразной.

Если переменная – путь, то первая производная скорость, а скорость изменения скорости – ускорение – это уже вторая производная.

Практическая польза понятия производной огромна.

Дело в том, что физические принципы мы не можем сформулировать иначе, как условия, накладываемые природой на скорости и ускорения процессов. Ярчайший пример – законы Ньютона. Когда мы применяем общие принципы к конкретным задачам, мы получаем дифференциальные уравнения, которые связывают неизвестную функцию с её, тоже неизвестными, производными.

Решая дифференциальные уравнения, мы находим закон движения и получаем возможность предсказывать развитие ситуации, например, полёт снаряда.

 

Введение

Назначение опорного конспекта – служить ключом для самостоятельной работы.

Заочник учится самостоятельно!(в основном!) Поэтому количество часов, отведенных на самостоятельную работу заочников очень велико, и информацию придётся брать из разных источников, в основном из интернета. Однако, обратившись к интернету, вы сразу обнаружите, что эти источники информации изобилуют деталями, предостережениями, примечаниями, описаниями особых случаев, и легко можно отвлечься и заблудиться в деталях. Кроме этого, сильно мешает и разнобой в обозначениях и названиях.

Много отличной переводной литературы по математике, но за рубежом своя терминологическая традиция, и с помощью интернета источники информации постоянно испытывают «перекрёстное опыление», что затуманивает картину.

Поэтому в данном опорном конспекте акцент сделан на показ общей картины наиболее кратким способом. Подробности, по мере надобности, возьмёте из интернета.

Опорный конспект поможет сориентироваться при первом чтении, чтобы студент мог быстро уловить суть предмета.

Главный совет: когда затрудняетесь понять, что означает близкие по звучанию термины, сначала принимайте на веру предположение, что они означают одно и то же. Ньюансы проявятся потом.

На первом курсе бакалавры втуза изучают по математике такие разделы:

 

1. Аналитическую геометрию,

2. линейную алгебру,

3. математический анализ.

 

Для усвоения этих (и дальнейших!) разделов математики следует использовать следующие идеи.

А. Идея изоморфизма. Если каждому элементу одного множества можно взаимно однозначно поставить в соответствие элемент другого множества, причем операции на первом множестве можно заменить эквивалентными операциями на втором, то мы спокойно можем рассматривать действия на первом множестве и переносить их результаты на элементы второго. Можно делать и наоборот, когда это удобнее.

Пример. Множество вещественных чисел и числовая ось. Каждому отрезку соответствует число, а каждому числу – отрезок. Поэтому при решении задач мы постоянно перескакиваем от рассмотрения на числовой оси к рассмотрению в виде десятичных дробей, и наоборот.

Б. Всякая теорема вначале была предположением, которое удалось доказать.

Пример. Теорема Пифагора.

В. Замкнутое относительно операций множество. Это такое множество, что операции, выполняемые на нём, снова порождают элементы этого же множества, то есть элементы, обладающие такими же свойствами. Это позволяет знания, полученные на отдельных примерах, переносить на все элементы множества. Пример. Линейное пространство – множество, замкнутое относительно операции «линейная комбинация», которая порождает всё указанное пространство, используя только п базисных векторов.

Г. Теория представлений. Она гласит, что в математике 90% успеха зависит от того, насколько удачное представление мы выберем для задачи.

Пример. Разнообразные дополнительные построения в геометрии. Если мы для доказательства теоремы Пифагора нарисуем «пифагоровы штаны», то доказательство будет сложнее, чем в случае, когда мы нарисуем трапецию.

Д. Любое условие любой математической задачи – это ограничение, наложенное на

переменные. Требуется найти те значения переменных, которые удовлетворяют ограничениям.

Основная идея аналитической геометрии – исследовать геометрические образы с помощью уравнений, введя систему координат и записав для каждой фигуры соответствующие уравнения или неравенства. При этом геометрическую интерпретацию решениям систем уравнений дают пересечения – как фигур между собой, так и с координатными плоскостями и осями.

Линейная алгебра выросла из факта, что математические закономерности, которые легко интерпретировать геометрически, можно перенести на системы уравнений со многими неизвестными, если ввести понятие N-мерного пространства.

Мостиком, соединяющим линейную алгебру и аналитическую геометрию, являются понятия линейной комбинации и линейной зависимости.

Математический анализ вырос из потребности делать астрономические и технические расчёты с неограниченной точностью, но так, чтобы избежать «проклятия вычислений»! Противоречивость этой задачи служит главной причиной «непонятной запутанности» матанализа и теоретической механики.

В дополнение к известным из элементарной математики действиям в матанализе вводится ещё одно действие – операция предельного перехода. Она позволяет доказывать теоремы, верные для любой точности расчётов, какая потребуется нам в будущем.

Очень важными понятиями в матанализе являются понятия переменной величины и непрерывной функции.

Переменная величина – это не число! Основное свойство числа – занимать твёрдо установленное место в ряду других чисел. Переменная величина может принимать разные значения из допустимого диапазона.

Вы найдёте множество определений понятия функции. Мы будем пользоваться в основном старомодным определением, что функция – это зависимая переменная.

Пример. Самолет выполняет фигуры высшего пилотажа. Лётчик по своей прихоти направляет его, то вверх, то вниз. Высота – независимая переменная. А давление воздуха за бортом? Оно зависит от высоты. Оно такое, каким быть ему предназначено законом природы.

Слово функция можно перевести как «назначение». Функционер – человек, который назначен и функционирует, то есть делает то, что ему назначено делать.

Непрерывная функция – такая, что неограниченно сближающимся значениям аргумента соответствуют неограниченно сближающиеся значения функции.

Понятие непрерывной функции – изобретение, позволяющее развивать математические теории, пригодные для любой точности измерений, которую позволяет технический прогресс. И причём в докомпьютерную эпоху.

Из матанализа выросла теория дифференциальных уравнений – вершина классической математики и физики вплоть до начала ХХ века. Схема проста: наблюдая изменяющиеся явления природы, записываем ограничения, которые накладывает природа на скорости изменений, в форме уравнений. Дифференциальных уравнений. Затем, решая уравнения, находим функции, описывающие явления природы в численной форме. Эти функции, в теоретической механике, например, так и величаются: «закон движения».

 

Синусы! Косинусы! Тангенсы! Котангенсы!

 

 

Линейная алгебра и аналитическая геометрия.

Линейные образы на плоскости

Уравнение прямой на плоскости в общем виде записывается:

A x + B y + C = 0 (1)

Это уравнение из всех точек плоскости выделяет только те, для координат которых справедливо указанное равенство.

Здесь А, В, С – любые рациональные числа, но А и В не равны нулю одновременно.

Для наглядности будем считать, что все они отличны от нуля.

Поделив на В, можно записать:

y = -A/B*x-C/B (2)

Введя обозначения k = -A/B, b = -C/B, (3)

получим уравнение прямой в привычном со школы виде:

y = k*x+b (4)

Важно понимать, что формулы (1) и (4) по сути одно и то же.

Запишем теперь два уравнения для двух прямых:

и (5)

Здесь мы поменяли обозначения по сравнению с формулами (1) и (4), так как в дальнейшем нам придется экономить буквы, иначе нам не хватит букв латинского алфавита.

– соответствует привычному обозначению х, а – привычному обозначению у.

Все объекты, которые можно описать уравнениями, похожими на уравнение прямой, принято называть линейными образами.

Объединив два уравнения скобочкой, получим систему двух уравнений с двумя неизвестными:

(6)

Слово «система» означает, что, когда мы ищем решения (числа, удовлетворяющие уравнениям) мы ищем такие числа, которые превращают в верные равенства ОДНОВРЕМЕННО ВСЕ уравнения системы.

Начертив графики, мы получим наглядную графическую иллюстрацию понятия «система линейных уравнений». Видно, что в зависимости от соотношений коэффициентов получаются:

1. две пересекающиеся прямые,

2. две параллельные прямые,

3. две совпадающие прямые.

 

1 случай. Система (6) имеет единственное решение. Координаты точки пересечения {x₁₀, x₂₀ } являются корнями системы. Эта точка удовлетворяет первому уравнению, так как лежит на его прямой, так и второму, так как лежит и на его прямой тоже.

2 случай. Система (6) не имеет решения, так как нет точек, координаты которых удовлетворяют одновременно обоим уравнениям..

3 случай. Система (6) имеет бесконечное множество решений, так как все точки, удовлетворяющие уравнению 1-й прямой, одновременно являются всеми точками, удовлетворяющими уравнению 2-й прямой.

 

Таблица коэффициентов системы (6)

(7)

называется квадратной матрицей 2-го порядка. Новое слово «матрица» ввели для того чтобы показать, что матрица – это НЕ ВООБЩЕ таблица, а таблица с определёнными свойствами.

- называется вектор-столбцом неизвестных,

- называется вектор-столбцом свободных членов.

В символическом виде система (6) перепишется:

(8)

Читается так: вектор-столбец неизвестных, умноженный на матрицу коэффициентов, равен вектор-столбцу свободных членов.

Часто вектор удобно записывать как вектор строку:

x = { } b = { }.

При записи в столбец больше наглядности по поводу выполняемых действий, при записи в строчку – больше экономии места.

Векторы изначально придумали для того, чтобы с их помощью описывать направленные величины в физике: скорость, ускорение, силу, и так далее. А потом, когда из этого получился эффективный матаппарат, понятие вектора внесли и в другие науки, например, в экономику, где их способность указывать направление зачастую не применяется никак.

Механика рассматривает три типа векторов: свободные, скользящие и закреплённые.

Если физический смысл не меняется от перенесения вектора из одной точки пространства в другую, то вектор – свободный.

Если физический смысл не меняется при скольжении вектора вдоль прямой, то вектор скользящий.

Если физический смысл меняется от какого-либо перенесения вектора, то его переносить нельзя, он является закреплённым. Однако все математические свойства векторов можно изучать, рассматривая только свободные векторы. Для простоты начало свободного вектора всегда помещается в начало координат. Поэтому в математике x = { } обозначает вектор, начало которого всегда в начале координат, а конец имеет координаты и .

Если вдоль оси направить единичный вектор i, а вдоль оси направить единичный вектор j, то вектор x можно представить в виде суммы:

x= (9)

Это называется разложением по базису. Вектора i и j называются базисными. Их длины равны единице.

Базис резко упрощает процедуры сложения, вычитания векторов, умножения векторов на число, а также позволяет изящно и просто ввести понятия скалярного, векторного и смешанного произведений векторов. Последние нужны для компактного описания законов физики.

- сумма векторов,

-произведение вектора на число,

Скалярное произведение двух векторов: (10)

Физический смысл скалярного произведения – работа.

Скалярное произведение двух перпендикулярных векторов равно нулю.

Это очень важное свойство, часто используется для того, чтобы аналитически отобразить перпендикулярность векторов..