Етсяфункция F(x), выражающая для каждого x вероятность того, что
Случайная величина X приметзначение, меньшее x
F(x) = P(X < x). Свойствафункции распределения1. Значенияфункциираспределенияпринадлежатотрезку [0, 1]. 
 – неубывающаяфункция.
– неубывающаяфункция.  при
при 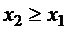
3. Вероятность того, чтослучайная величина приметзначение, заключенное в интервале (a, b), равнаприращениюфункциираспределения на этоминтервале.  4. На минусбесконечностифункцияраспределенияравна нулю, на плюс бесконечностифункцияраспределенияравна единице.5. Вероятность того, чтонепрерывнаяслучайная величина
4. На минусбесконечностифункцияраспределенияравна нулю, на плюс бесконечностифункцияраспределенияравна единице.5. Вероятность того, чтонепрерывнаяслучайная величина  примет одно определенноезначение, равна нулю.
примет одно определенноезначение, равна нулю.
24.
Определение.Плотностьюраспределения вероятностейнепрерывнойслучайнойвеличины  называетсяфункция f(x) – перваяпроизводная от функциираспределения
называетсяфункция f(x) – перваяпроизводная от функциираспределения  .
.  Свойстваплотностираспределения
Свойстваплотностираспределения
 1. Плотностьраспределения – неотрицательнаяфункция.
1. Плотностьраспределения – неотрицательнаяфункция. 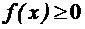 2. Несобственныйинтеграл от плотностираспределения в пределах от - ¥ до ¥равенединице.
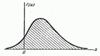
2. Несобственныйинтеграл от плотностираспределения в пределах от - ¥ до ¥равенединице.  Криваяраспределениявероятностей - кривая, характеризующаяраспределениевероятностейпоявлениявеличиныгидрологическогоэлемента. Кривая, изображающаяплотностьраспределенияслучайнойвеличины, называетсякривойраспределения
Криваяраспределениявероятностей - кривая, характеризующаяраспределениевероятностейпоявлениявеличиныгидрологическогоэлемента. Кривая, изображающаяплотностьраспределенияслучайнойвеличины, называетсякривойраспределения
Рассматривая плотность распределения  для одной случайной величины, мы ввели понятие «элемента вероятности»
для одной случайной величины, мы ввели понятие «элемента вероятности»  . Это есть вероятность попадания случайной величины
. Это есть вероятность попадания случайной величины 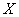 на элементарный участок
на элементарный участок  , прилегающий к точке
, прилегающий к точке  . Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение
. Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение  .Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами
.Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами  ,
,  , примыкающий к точке
, примыкающий к точке 
25. Дискретнаяс.в. – это с.в., принимающая конечное или счетное число значений.1).Мат. Ожидание:  Свойства: Mc=c, c=const; Mcx=cMx; M(x+y)=M(x)+M(y);M(xy)=MxMy;
Свойства: Mc=c, c=const; Mcx=cMx; M(x+y)=M(x)+M(y);M(xy)=MxMy;
2).Дисперсия-среднее значение квадрата отклонения с.в. от ее среднего значения.Dx=Mx2–(Mx)2. Свойства: Dc=o, c=const; Dcx=c2Dx; D(x+y)=Dx + Dy; 3). Среднее квадр. Отклонение –  . 4).Модой с.в. х наз. число М0, которое равно её наиболее вероятному значению.
. 4).Модой с.в. х наз. число М0, которое равно её наиболее вероятному значению.  ; 5).Медианой с.в. наз. такое число, что:
; 5).Медианой с.в. наз. такое число, что:

27 Мода и медиана с.в.
Мода д.с.в. – это наиболее вероятное значение с.в.; для н.с.в. – это точка максимума плотности распределения. Обозначение: Мoх.
Медиана Мeх с.в. - это такое значение с.в., для которого P { X < xm }= P { X > xm }=1/2
Медиана является характеристикой н.с.в..
Геометрически медиана- это точка на оси 0 x для которой площади под графиком плотности распределения, лежащие слева и справа от нее, одинаковы и равны 21.
Если плотность распределения симметрична относительно прямой x = a и распределение одномодально, то математическое ожидание, медиана и мода совпадают между собой,
M (X)= Mex=M О x

28 Свойства математического ожидания и дисперсии случайной величины.
свойствадисперсиии.
1. D(X) ≥0
2. D(c) =0
3. D(cX)=c 2 D(X)
4 D(X+Y)=D(X)+D(Y) где( Х, Y - независимые с.в.)
5 D(X+с)= D(X)
1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Свойства мат ожидания
M[C] = C.
M[CX] = CM[X].
M[XY ] = M[X]M[Y ].
M[X + Y ] = M[X] +M[Y ]
M[X] = np(произведение числа ожиданий на вероятность)
29. Начальные и центральные моменты дискретной с.в. Коэффициент асимметрии, эксцесс.
В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.
Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x, т.е. a k = Mx k.
Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx)k.
Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a 1 = Mx, а дисперсия - центральный момент второго порядка,
a 2 = Mx 2 = M(x - Mx)2 = Dx.
Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:
m 2=a 2-a 12, m 3 = a 3 - 3a 2a 1 + 2a 13.
Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx, то все ее центральные моменты нечетного порядка равны нулю.
В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой,
где m 3 - центральный момент третьего порядка, - среднеквадратичное отклонение.
Эксцесс Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x, от нормального распределения, является эксцесс.
Эксцесс g случайной величины x определяется равенством.
У нормального распределения, естественно, g = 0. Если g (x)> 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.
30. Бернуллиевскаяс.в., ее математическое ожидание и дисперсия.
Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность  , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
Мх=npDx=npqq=1-p
31 Пуассоновская с.в., ее математическое ожидание и дисперсия.
Случайная величина имеет распределение Пуассона с параметром альфа (альфа > 0), если

Что кратко записывается в виде L(кси) = П(кси); при этом альфа= Мх = Dх.
Альфа = np
Закон распределения называется равномерным, если

ф-цияраспред.: 
 ,
, 
Случайная величина распределена по показательному закону, если
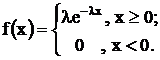
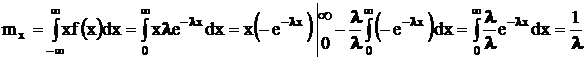 ;
;
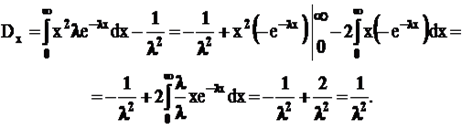
36. Случайная величина распределена по нормальному закону распределения, если  ;
;  .Нормально распределенная случайная величина X имеет математическое ожидание, равное нулюДисперсия определяет форму кривой нормального закона распределения.
.Нормально распределенная случайная величина X имеет математическое ожидание, равное нулюДисперсия определяет форму кривой нормального закона распределения.
Чаще всего используют нормальный закон в нормированной форме, который получают заменой переменной  .
. 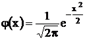 .
.
 ; для
; для 
 ;
;  .
.
37.Известно, что если случайная величина X задана плотностью распределения  , то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:
, то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:  .
.
Пусть случайная величина X распределена по нормальному закону. Тогда  .
.
Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную 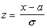 . Отсюда
. Отсюда  .
.
Найдем новые пределы интегрирования. Если  , то
, то  , если
, если  , то
, то  . Тогда
. Тогда

 .
.
Выражение  , входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:
, входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:
 Ф
Ф 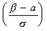 — Ф
— Ф  ,
,
где Ф(x) =  .
.
Эту формулу называют формулой Лапласа.
Если случайная величина X является признаком генеральной совокупности, то формула Лапласа дает долю элементов генеральной совокупности, у которых значение признака X находится в границах от 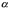 до
до  .
.
Интеграл, через который выражается функция Лапласа, нельзя выразить через элементарные функции. Его можно представить в виде степенного ряда, если разложить в ряд подынтегральную функцию  и почленно проинтегрировать ряд. Тогда
и почленно проинтегрировать ряд. Тогда
Ф(x) =  .
.
C помощью этого ряда можно вычислить значение Ф(x) для любого x с любой точностью. Составлены специальные таблицы значений функции Лапласа.
Отметим ряд свойств функции Лапласа, полезных для применения.
1. Функция Ф(x) – нечетная, т. е. Ф(-x) = –Ф(x).
2. Функция Ф(x) – возрастающая, быстро приближающаяся к своему пределу, равному 0,5: Ф(0) = 0, Ф(1) = 0,3413, Ф(2) = 0,4772, Ф(3) = 0,4986, Ф(4) = 0,4999 и т.д. На практике полагают Ф(x)  для x>5.
для x>5.




 – неубывающаяфункция.
– неубывающаяфункция.  при
при 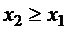
 4. На минусбесконечностифункцияраспределенияравна нулю, на плюс бесконечностифункцияраспределенияравна единице.5. Вероятность того, чтонепрерывнаяслучайная величина
4. На минусбесконечностифункцияраспределенияравна нулю, на плюс бесконечностифункцияраспределенияравна единице.5. Вероятность того, чтонепрерывнаяслучайная величина  примет одно определенноезначение, равна нулю.
примет одно определенноезначение, равна нулю. Свойстваплотностираспределения
Свойстваплотностираспределения 1. Плотностьраспределения – неотрицательнаяфункция.
1. Плотностьраспределения – неотрицательнаяфункция. 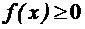 2. Несобственныйинтеграл от плотностираспределения в пределах от - ¥ до ¥равенединице.
2. Несобственныйинтеграл от плотностираспределения в пределах от - ¥ до ¥равенединице.  Криваяраспределениявероятностей - кривая, характеризующаяраспределениевероятностейпоявлениявеличиныгидрологическогоэлемента. Кривая, изображающаяплотностьраспределенияслучайнойвеличины, называетсякривойраспределения
Криваяраспределениявероятностей - кривая, характеризующаяраспределениевероятностейпоявлениявеличиныгидрологическогоэлемента. Кривая, изображающаяплотностьраспределенияслучайнойвеличины, называетсякривойраспределения для одной случайной величины, мы ввели понятие «элемента вероятности»
для одной случайной величины, мы ввели понятие «элемента вероятности»  . Это есть вероятность попадания случайной величины
. Это есть вероятность попадания случайной величины 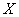 на элементарный участок
на элементарный участок  , прилегающий к точке
, прилегающий к точке  . Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение
. Аналогичное понятие «элемента вероятности» вводится и для системы двух величин. Элементом вероятности в данном случае называется выражение  .Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами
.Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами  , примыкающий к точке
, примыкающий к точке 
 Свойства: Mc=c, c=const; Mcx=cMx; M(x+y)=M(x)+M(y);M(xy)=MxMy;
Свойства: Mc=c, c=const; Mcx=cMx; M(x+y)=M(x)+M(y);M(xy)=MxMy; . 4).Модой с.в. х наз. число М0, которое равно её наиболее вероятному значению.
. 4).Модой с.в. х наз. число М0, которое равно её наиболее вероятному значению.  ; 5).Медианой с.в. наз. такое число, что:
; 5).Медианой с.в. наз. такое число, что:

 , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.


 ,
, 
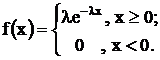
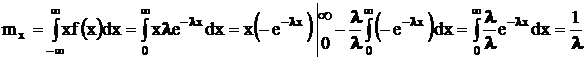 ;
;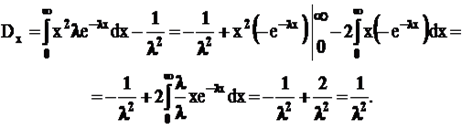
 ;
;  .Нормально распределенная случайная величина X имеет математическое ожидание, равное нулюДисперсия определяет форму кривой нормального закона распределения.
.Нормально распределенная случайная величина X имеет математическое ожидание, равное нулюДисперсия определяет форму кривой нормального закона распределения. .
. 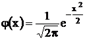 .
. ; для
; для 
 ;
;  .
. , то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:
, то вероятность того, что X примет значение, принадлежащее интервалу (a,b), такова:  .
. .
.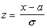 . Отсюда
. Отсюда  .
. , то
, то  , если
, если  , то
, то  . Тогда
. Тогда
 .
. , входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:
, входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем: Ф
Ф 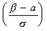 — Ф
— Ф  ,
, .
.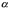 до
до  .
. и почленно проинтегрировать ряд. Тогда
и почленно проинтегрировать ряд. Тогда .
. для x>5.
для x>5.

