ПРИЛОЖЕНИЯ
Контрольное задание №1.……………………….……………………………64
Контрольное задание №2.……………………….……………………………66
Контрольное задание №3.……………………….……………………………67
Литература…………………………………………………...………………..70
ВВЕДЕНИЕ
Наиболее простым методом преобразования систем линейных уравнений традиционно считается метод Гаусса-Жордана. При помощи данного метода можно найти единственное решение системы линейных уравнений или доказать его отсутствие. А в том случае, когда система имеет бесчисленное множество решений, метод Гаусса-Жордана позволяет находить базисные решения системы и переходить всего за один шаг от одного базисного решения к другому. Такая особенность метода Гаусса-Жордана позволила на его основе реализовать так называемый симплекс-метод решения задач линейного программирования.
Однако существует еще один метод преобразования систем линейных уравнений – метод жордановых исключений. По существу, это хорошо всем нам знакомый метод исключения неизвестных. Однако практическая реализация данного метода в виде жордановых таблиц позволила существенно сократить арифметические вычисления. Это заметно даже при решении задач линейной алгебры. Но особенно это заметно во время решения задач математического программирования. Применительно к задачам линейного программирования, метод жордановых исключений получил название метода Штифеля.
Метод Штифеля успешно применяется в математическом программировании не только потому, что он существенно проще традиционного симплекс-метода. Самое главное его достоинство заключается в том, что он позволяет примерно вдвое сократить количество учебных часов, необходимых преподавателю для прочтения курса линейного программирования.
Пособие состоит из четырех частей. В первой части изучаются методы жордановых исключений и модифицированных жордановых исключений. Данные методы преобразования систем линейных равенств оформляются в виде жордановых таблиц. Приведены и доказаны алгоритмы перехода от одной жордановой таблицы к другой (один шаг жордановых исключений).
Во второй главе изучаются применение метода жордановых исключений в линейной алгебре. Применение метода жордановых исключения к решению стандартных задач линейной алгебры оказалось вполне оправданным. На примерах доказано, что решение таких задач, как вычисление ранга матрицы, нахождение обратной матрицы и решение систем линейных уравнений методом жордановых исключений оказалось проще, чем решение традиционными методами.
В третьей и четвертой главе данного пособия содержится краткое изложение курса математического программирования, основанного на методе жордановых исключений (метод Штифеля).
Пособие, прежде всего, предназначено для студентов математических факультетов, получающих специальность «Преподаватель». Данное пособие также полезно студентам экономических и других специальностей, изучающих математическое программирование и линейную алгебру.
ГЛАВА I
МЕТОД ЖОРДАНОВЫХ ИСКЛЮЧЕНИЙ
Вычисление ранга матрицы. Нахождение линейной
Зависимости между векторами
Докажем вначале следующую теорему:
Теорема 2.1 (Стейница). Если в жордановой таблице все строки линейно независимы и их количество не превосходит количества столбцов (m £ n), то в результате m последовательных шагов жордановых исключений можно переместить наверх все yj (j = 1, 2,…, m).
Доказательство. Помешать переброске наверх переменной yj может невозможность выбора разрешающего элемента, то есть равенство нулю соответствующих элементов j -ой строки. Предположим, что после k шагов метода жордановых исключений (k < m) мы пришли к следующей таблице:
|
| y 1
| y 2
| …
| yk
| xk+ 1
| …
| xn
|
| x 1
| b 11
| b 12
| …
| b 1 k
| b 1, k +1
| …
| b 1 n
|
| x 2
| b 21
| b 22
| …
| b 2 k
| b 2, k +1
| …
| b 2 n
|
| …
| ……………………………………….
| …………………………….
|
| xk
| bk 1
| bk 2
| …
| bkk
| bk, k +1
| …
| bkn
|
| yk+ 1
| bk +1, 1
| bk +1, 2
| …
| bk +1, k
|
| …
|
|
| yk+ 2
| bk +2, 1
| bk +2, 2
| …
| bk +2, k
|
| …
|
|
| …
| ……………………………………….
| …………………………….
|
| ym
| bm 1
| bm 2
| …
| bmk
|
| …
|
|
Табл. 2.1.
Если переменные yk+ 1, yk+ 2,…, ym дальше перебрасывать наверх нельзя, то это означает, что соответствующие разрешающие элементы, расположенные в правом нижнем углу таблицы, равны нулю. Но в этом случае переменные yk+ 1, yk+ 2,…, ym линейно выражаются через
y 1, y 2,…, yk. Действительно:
yk+ 1 = bk +1, 1 ´ y 1+ bk +1, 2 ´ y 2 +…+ bk +1, k ´ yk,
yk+ 2 = bk +2, 1 ´ y 1+ bk +2, 2 ´ y 2 +…+ bk +2, k ´ yk,
……………………………………………….
ym = bm 1 ´ y 1 + bm 2 ´ y 2 +…+ bmk ´ yk.
Полученное противоречие доказывает то, что все игреки можно перенести наверх, что и требовалось доказать. Рассмотрим два примера.
Пример 2.1. Вычислить ранг матрицы 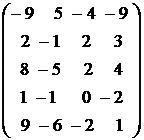 .
.
Решение. Составим для этой матрицы жорданову таблицу (таблица 2.2). Будем переносить переменные xi наверх, пока это возможно. По теореме Стейница в верхнюю часть таблицы можно переместить столько переменных из левого заглавного столбца, сколько в таблице линейно независимых строк. А это и есть ранг матрицы.
|
| y 1
| y 2
| y 3
| y 4
|
|
| y 1
| x 2
| y 3
| y 4
|
| x 1
| –9
|
| –4
| –9
|
| x 1
|
| –5
|
|
|
| x 2
|
| –1
|
|
|
| y 2
|
| –1
|
|
|
| x 3
|
| –5
|
|
|
| x 3
| –2
|
| –8
| –11
|
| x 4
|
| –1
|
| –2
|
| x 4
| –1
|
| –2
| –5
|
| x 5
|
| –6
| –2
|
|
| x 5
| –3
|
| –14
| –17
|
Табл. 2.2. Табл. 2.3.
При переходе от таблицы 2.2 к таблице 2.3 в качестве разрешающей строки и разрешающего столбца выбраны вторая строка и второй столбец (разрешающий элемент a 22 = –1) и так далее. После трех шагов метода обыкновенных жордановых исключений мы придем к таблице 2.5:
|
| x 1
| x 2
| y 3
| y 4
|
|
| x 1
| x 2
| x 3
| y 4
|
| y 1
|
|
| –6
| –6
|
| y 1
| –2
| –2,5
| –1,5
| –4,5
|
| y 2
|
|
| –10
| –9
|
| y 2
| –3
| –3,5
| –2,5
| –6,5
|
| x 3
| –2
| –5
|
|
|
| y 3
| 0,5
| 1,25
| 0,25
| –0,25
|
| x 4
| –1
| –4
|
|
|
| x 4
|
|
|
|
|
| x 5
| -3
| -9
|
|
|
| x 5
| -1
| -4
|
|
|
Табл. 2.4. Табл. 2.5.
Дальнейший перевод переменных наверх невозможен из-за равенства нулю соответствующих разрешающих элементов (b 44 = b 54 = 0). Следовательно, по теореме Стейница ранг матрицы равен трем. Заметим, что кроме ранга матрицы мы попутно нашли зависимость между ее строками. Действительно, из последних двух строк таблицы 2.5 получим:
x 4 = 1 ´ x 1+ 1 ´ x 2 + 1´ x 3 = x 1 + x 2 + x 3,
x 5 = – 1 ´ x 1 – 4 ´ x 2 + 1´ x 3 = – x 1 – 4 x 2 + x 3.
Из последних равенств вытекает то, что четвертая строка исходной матрицы равна сумме первых трех строк, а пятая строка равна третьей строке минус первая строка и минус вторая строка, умноженная на четыре.
Пример 2.2. Проверить, являются ли векторы a 1 = (6; 8; – 2; – 1),
a 2 = (4; 2; – 2; 1), a 3 = (1; 3; 0; – 1) и a 4 = (– 7; – 1; 4; – 3) – линейно независимыми. В случае отрицательного ответа, указать соответствующую зависимость.
Решение. Линейная зависимость между векторами эквивалентна линейной зависимости между строками матрицы 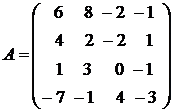 , составленной из координат этих векторов. Таким образом, данная задача решается аналогично задаче о нахождении ранга матрицы. Составим исходную жорданову таблицу 2.6 и сделаем два шага методом обыкновенных жордановых исключений, выбрав в качестве разрешающих элементов соответственно a 31 = 1 и b 23 = – 2. В результате приходим к таблице 2.8:
, составленной из координат этих векторов. Таким образом, данная задача решается аналогично задаче о нахождении ранга матрицы. Составим исходную жорданову таблицу 2.6 и сделаем два шага методом обыкновенных жордановых исключений, выбрав в качестве разрешающих элементов соответственно a 31 = 1 и b 23 = – 2. В результате приходим к таблице 2.8:
|
| y 1
| y 2
| y 3
| y 4
|
|
| x 3
| y 2
| y 3
| y 4
|
| x 1
|
|
| –2
| –1
|
| x 1
|
| –10
| –2
|
|
| x 2
|
|
| –2
|
|
| x 2
|
| –10
| –2
|
|
| x 3
|
|
|
| –1
|
| y 1
|
| –3
|
|
|
| x 4
| –7
| –1
|
| –3
|
| x 4
| –7
|
|
| –10
|
Табл. 2.6. Табл. 2.7.
|
| x 3
| y 2
| x 2
| y 4
|
| x 1
|
|
|
|
|
| y 3
|
| –5
| –0,5
| 2,5
|
| y 1
|
| –3
|
|
|
| x 4
|
|
| –2
|
|
Табл. 2.8.
Дальнейший перевод иксов наверх невозможен из-за равенства нулю соответствующих разрешающих элементов. Следовательно, векторы
a 1, a 2, a 3, a 4, являются линейно зависимыми. Причем a 1 = 2 a 3 + a 2,
a 4 = a 3 – 2 a 2. Последние соотношения видны из первой и четвертой строки таблицы 2.8.
Жордановых исключений
Заметим, что при решении системы линейных уравнений (2.1) первым способом мы попутно нашли еще и обратную матрицу к основной матрице системы (2.1). Действительно, запишем систему линейных уравнений (2.1) и систему, соответствующую таблице 2.12, в матричном виде:
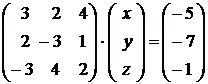 . (2.7)
. (2.7)
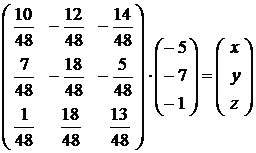 . (2.8)
. (2.8)
Заметим, что при написании системы (2.8) нам пришлось поменять местами вторую и третью строки и второй и третий столбцы таблицы 2.12. Это было сделано для того, чтобы не поменялись местами координаты векторов x = (x; y; z) и b = (–5; –7; –1).
Равенства (2.7) и (2.8) говорят о том, что матрицы
 и
и 
являются взаимно обратными.
Непосредственную проверку предлагается сделать читателям.
Пример 2.8. Найти матрицу, обратную к матрице
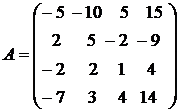 .
.
Решение. Матрицу А можно рассматривать как основную матрицу системы:
–5 x 1 – 10 x 2 +5 x 3 + 15 x 4 = y 1
2 x 1 + 5 x 2 – 2 x 3 – 9 x 4 = y 2
–2 x 1 + 2 x 2 + x 3 + 4 x 4 = y 3 (2.9)
–7 x 1 + 3 x 2 + 4 x 3 + 14 x 4 = y 4.
Преобразуем систему (2.9) методом обыкновенных жордановых исключений, последовательно выражая переменные xi через yj:
|
| y 1
| y 2
| y 3
| y 4
|
|
| y 1
| y 2
| x 3
| y 4
|
| x 1
| –5
| –10
|
|
|
| x 1
|
| –20
|
| –5
|
| x 2
|
|
| –2
| –9
|
| x 2
| –2
|
| –2
| –1
|
| x 3
| –2
|
|
|
|
| y 3
|
| –2
|
| –4
|
| x 4
| –7
|
|
|
|
| x 4
|
| –5
|
| –2
|
Табл. 2.44. Табл. 2.45.
|
| x 4
| y 2
| x 3
| y 4
|
|
| x 4
| x 2
| x 3
| y 4
|
| x 1
|
|
| –15
|
|
| x 1
| –5
| –5
|
| –20
|
| x 2
| –2
| –1
|
| –5
|
| y 2
| –2
| –1
|
| –5
|
| y 3
|
|
| –7
|
|
| y 3
| –14
| –8
|
| –40
|
| y 1
|
|
| –4
|
|
| y 1
| –9
| –5
|
| –23
|
Табл. 2.46. Табл. 2.47.
После четырех шагов метода обыкновенных жордановых исключений все переменные yj оказываются в левом заглавном столбце таблицы 2.48. Поменяем местами первую и четвертую строки и первый и четвертый столбцы. В таблице 2.49 переменные xi и yj расположены в порядке возрастания индексов.
|
| x 4
| x 2
| x 3
| x 1
|
|
| x 1
| x 2
| x 3
| x 4
|
| y 4
| –0,25
| –0,25
| 0,75
| –0,05
|
| y 1
| 1,15
| 0,75
| 8,75
| –3,25
|
| y 2
| –0,75
| 0,25
| 2,25
| 0,25
|
| y 2
| 0,25
| 0,25
| 2,25
| –0,75
|
| y 3
| –4
|
|
|
|
| y 3
|
|
|
| –4
|
| y 1
| –3,25
| 0,75
| 8,75
| 1,15
|
| y 4
| –0,05
| –0,25
| 0,75
| –0,25
|
Табл. 2.48. Табл. 2.49.
Таким образом, мы нашли обратную матрицу:
 .
.
Замечание. Для того чтобы в последней таблице не менять сроки и столбцы местами, достаточно разрешающий элемент всегда выбирать на главной диагонали таблицы. Тогда на каждом шаге меняются местами переменные с одинаковыми индексами (xi меняется на yi).
ГЛАВА III
Применение метода модифицированных
жордановых исключений в линейном
программировании
Описание метода Штифеля
Основной задачей линейного программирования, при решении которой используется метод жордановых исключений, является стандартная задача. Напомним, что задача называется стандартной, если все ограничения задачи являются неравенствами и при этом все переменные ограничены на знак. Любая другая задача тем же методом жордановых исключений предварительно сводится к стандартной. При этом сама задача существенно упрощается. Предположим, сначала, что решается основная, т.е. стандартная задача линейного программирования:
z (X) = c 1 x 1 + c 2 x 2 +…+ cjxj +…+ cnxn ® max (3.3)
a 11 x 1 + a 12 x 2 +…+ a 1 jxj +…+ a 1 nxn £ b 1
……………………………………………
ai 1 x 1 + ai 2 x 2 +…+ aijxj +…+ ainxn £ bi (3.4)
……………………………………………
am 1 x 1 + am 2 x 2 +…+ amjxj +…+ amnxn £ bm
x 1; x 2; … xj; … xn ³ 0
Введем в систему (3.4) m дополнительных, ограниченных на знак переменных. Для этого перенесем все слагаемые из левых частей неравенств (3.4) в правые:
y 1 = b 1+ a 11(– x 1) + a 12(– x 2) +…+ a 1 j (– xj) +…+ a 1 n (– xn),
……………………………………………………………….
yi = bi + ai 1(– x 1) + ai 2(– x 2) +…+ aij (– xj) +…+ ain (– xn), (3.5)
……………………………………………………………….
ym = bm + am 1(– x 1) + am 2(– x 2) +…+ amj (– xj) +…+ amn (– xn),
x 1; x 2; … xn; y 1; y 2; … ym ³ 0.
Отметим, что введение дополнительных переменных увеличит будущую расчетную таблицу всего на один столбец. Обойтись без введения дополнительных переменных нельзя, т.к. в дальнейшем мы будем следить их знаками для того, чтобы не выйти из области планов задачи (3.3) – (3.5).
При решении задачи нам предстоит несколько раз преобразовывать систему (3.3) – (3.5) методом модифицированных жордановых исключений. Вычисления так же, как и раньше, будем оформлять в виде жордановых таблиц:
|
| – x 1
| – x 2
| …
| – xj
| …
| – xn
|
|
| y 1
| a 11
| a 12
| …
| a 1 j
| …
| a 1 n
| b 1
|
| …
| ……………………………………………
| …
|
| yi
| ai 1
| ai 2
| …
| aij
| …
| ain
| bi
|
| …
| ……………………………………………
| …
|
| ym
| am 1
| am 2
| …
| amj
| …
| amn
| bm
|
| z
| – c 1
| – c 2
| …
| – cj
| …
| – cn
|
|
Табл. 3.1.
Верхние строки таблицы соответствуют системе ограничений задачи, а нижнюю строку мы зарезервируем за функцией цели. Именно эта строка таблицы и будет играть ключевую роль в решении задачи. В дальнейшем элементы последней строки жордановой таблицы мы будем называть оценками соответствующих свободных переменных. В исходной таблице 3.1 числа -c 1, -c 2,…, -cj,…, -cn являются оценками свободных переменных x 1, x 2,…, xj,…, xn, соответственно.
Свободными переменными мы в дальнейшем будем называть переменные, расположенные в верхней заглавной строке жордановой таблицы. На первом этапе решения задачи это переменные x 1,…, xn. Придавая свободным переменным различные значения, мы каждый раз будем получать различные значения зависимых (базисных) переменных (на первом этапе, это переменные y 1,…, ym). В частности, придавая свободным переменным нулевые значения, мы получаем так называемые базисные решения системы (3.5). Исходным базисным решением является вектор
(0,…, 0,…, 0, b 1,…, bi,…, bm).
Причем лишь те решения (x 1,…, xn, y 1,…, ym) системы ограничений являются планами исходной задачи (3.3) – (3.5), все компоненты которых ограничены на знак (xj ³ 0, yi ³ 0, j = 1, 2,…, n, i = 1, 2,…, m). Базисные решения системы ограничений (3.5), являющиеся планами (т.е. ограниченные на знак), называются опорными планами задачи (3.3) – (3.5). В дальнейшем мы увидим, что оптимальный план задачи, если он существует, находится среди опорных планов.
Данный факт можно установить без использования теории выпуклых множеств. Просто мы будем искать наилучший с точки зрения максимума целевой функции план среди опорных планов задачи (3.3) – (3.5). А затем мы докажем, что среди неопорных планов задачи нет плана, лучшего, чем найденный опорный план.
Среди правых частей b 1,…, bi,…, bm системы ограничений (3.5) могут оказаться отрицательные числа. Поэтому исходное базисное решение (0,…, 0,…, 0, b 1,…, bi,…, bm) системы ограничений (3.5), найденное из таблицы 3.1, как правило, не является планом задачи. Данное обстоятельство приводит нас к необходимости решать задачу в два этапа. На первом этапе мы выходим в область планов исходной задачи (3.3) – (3.5) или доказываем, что задача не имеет решения из-за отсутствия планов. На втором этапе мы находим оптимальный план или доказываем неразрешимость задачи из-за неограниченности функции цели.
Оба этапа осуществляются с помощью метода модифицированных жордановых исключений, который применительно к решению задач линейного программирования получил название метода Штифеля. В отличие от решения систем линейных уравнений, на каждом шаге разрешающий элемент выбирается не произвольно, а исходя из конкретных целей. Причем при выборе разрешающего элемента мы неуклонно будем соблюдать принцип минимального симплексного отношения. Данный принцип вытекает из теоремы о минимальном симплексном отношении.
Зафиксируем j -й столбец жордановой таблицы (3.1). Для тех элементов aij данного столбца, знак которых совпадает со знаком свободного члена bi, расположенного в той же строке, что и aij, определим отношение:
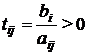 .
.
Числа 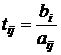 называются симплексными отношениями. Из определения следует, что все симплексные отношения строго больше нуля.
называются симплексными отношениями. Из определения следует, что все симплексные отношения строго больше нуля.
Предположим, что нам по какой-то причине захотелось выбрать разрешающий элемент в j -ом столбце. Переберем все элементы j -ого столбца и выберем в качестве разрешающего элемента тот элемент aij, для которого симплексное отношение 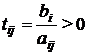 минимально. В этом случае говорят, что разрешающий элемент выбран по наименьшему симплексному отношению.
минимально. В этом случае говорят, что разрешающий элемент выбран по наименьшему симплексному отношению.
Теорема 3.1 (о минимальном симплексном отношении). Если разрешающий элемент в фиксированном столбце выбирать по наименьшему симплексному отношению, то после шага модифицированных жордановых исключений свободный член в разрешающей строке всегда становится положительным, а остальные свободные члены сохраняют свои знаки.
Доказательство. Предположим, что минимальное симплексное отношение в выбранном j -ом столбце соответствует r -ой строке. То есть
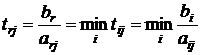 , (3.6)
, (3.6)
где минимум берется по тем i, для которых 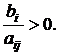 Тогда в качестве разрешающего элемента выберем элемент arj. Первое утверждение теоремы очевидно, так как после шага модифицированных жордановых исключений свободный член в разрешающей строке по формуле (1.10) будет равен
Тогда в качестве разрешающего элемента выберем элемент arj. Первое утверждение теоремы очевидно, так как после шага модифицированных жордановых исключений свободный член в разрешающей строке по формуле (1.10) будет равен 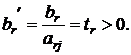
Выясним теперь, как изменяется свободный член в произвольной i –ой строке (i ¹ r). Для этого вспомним, что после одного шага модифицированных жордановых исключений свободный член, так же как и любой другой элемент жордановой таблицы, не попавший в разрешающие строку и столбец, вычисляется по формуле (1.12):
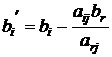 . (3.7)
. (3.7)
Рассмотрим три случая:
1. bi > 0. Если при этом aij = 0, то 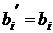 . То есть свободный член не изменился не только по знаку, но и по абсолютной величине. Если
. То есть свободный член не изменился не только по знаку, но и по абсолютной величине. Если
aij ¹ 0, то формулу (3.7) можно преобразовать к виду:
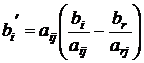 . (3.8)
. (3.8)
Если aij > 0, то 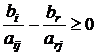 , так как
, так как 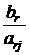 – минимальное симплексное отношение, а
– минимальное симплексное отношение, а 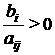 – произвольное симплексное отношение. Следовательно, в данной ситуации
– произвольное симплексное отношение. Следовательно, в данной ситуации 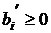 , как произведение двух неотрицательных чисел. То есть знак
, как произведение двух неотрицательных чисел. То есть знак 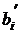 совпадает со знаком bi.
совпадает со знаком bi.
Если aij < 0, то скобка в равенстве (3.8) будет отрицательной, так как оба составляющие ее слагаемые строго меньше нуля. Следовательно, и в этом случае знак 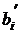 совпадает со знаком bi, так как произведение двух отрицательных чисел – положительно.
совпадает со знаком bi, так как произведение двух отрицательных чисел – положительно.
2. bi < 0. Если при этом aij = 0, то по-прежнему 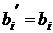 , т.е. знаки
, т.е. знаки 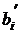 и bi совпадают. Если aij ¹ 0, то вновь воспользуемся формулой (3.8).
и bi совпадают. Если aij ¹ 0, то вновь воспользуемся формулой (3.8).
Если aij < 0, то 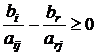 , так как
, так как 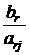 – минимальное симплексное отношение, а
– минимальное симплексное отношение, а 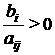 – произвольное симплексное отношение. Следовательно, в данной ситуации
– произвольное симплексное отношение. Следовательно, в данной ситуации  , как произведение противоположных по знаку чисел. То есть знак
, как произведение противоположных по знаку чисел. То есть знак 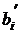 совпадает со знаком bi.
совпадает со знаком bi.
Если aij > 0, то скобка в равенстве (3.8) будет отрицательной, так как оба составляющие ее слагаемые строго меньше нуля. Следовательно, и в этом случае знак 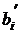 будет отрицательным и, следовательно, совпадает со знаком bi.
будет отрицательным и, следовательно, совпадает со знаком bi.
3. bi = 0. В данном случае после одного шага модифицированных жордановых исключений знак свободного члена 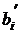 может стать как положительным, так и отрицательным. Точнее, из формулы (3.7) следует, что знак
может стать как положительным, так и отрицательным. Точнее, из формулы (3.7) следует, что знак 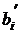 будет противоположен знаку aij. Так как число 0 можно считать как положительным, так и отрицательным, то и в этом случае можно считать, что знак
будет противоположен знаку aij. Так как число 0 можно считать как положительным, так и отрицательным, то и в этом случае можно считать, что знак 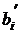 совпадает со знаком bi. Теорема доказана.
совпадает со знаком bi. Теорема доказана.
§3 Нахождение первоначального опорного плана
Перейдем непосредственно к первому этапу решения основной (стандартной) задачи линейного программирования, заданной таблицей 3.1. Напомним, что на первом этапе нам предстоит найти один из опорных планов или доказать, что задача не имеет планов и, следовательно, не имеет решения. При этом возможны две ситуации:
Пусть в столбце свободных членов нет ни одного отрицательного числа, т. е. 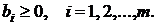 В данном случае первоначальное базисное решение (0,…, 0,…, 0, b 1,…, bi,…, bm), получающееся из таблицы 3.1, сразу является опорным планом задачи. Мы можем переходить ко второму этапу, т.е. к поиску оптимального плана.
В данном случае первоначальное базисное решение (0,…, 0,…, 0, b 1,…, bi,…, bm), получающееся из таблицы 3.1, сразу является опорным планом задачи. Мы можем переходить ко второму этапу, т.е. к поиску оптимального плана.
Если среди свободных членов есть отрицательные числа, то от них избавляются с помощью конечного числа шагов метода Штифеля. Рассмотрим подробнее, как это делается. Пусть, например, br < 0. Найдем j –й столбец, содержащий отрицательный элемент arj в r –ой строке. Здесь возможны два случая.
1. Такого столбца не существует, т.е. все элементы r –ой строки неотрицательны (arj ³ 0, j = 1, 2,…, n). В данном случае мы можем сделать вывод о том, что задача не имеет решения из-за отсутствия планов. Действительно, рассматривая r – ю строку таблицы 3.1, мы приходим к выводу о том, что переменная yr не может быть неотрицательной ни при каких неотрицательных значениях переменных x 1, x 2,…, xn:
yr = br + ar 1(- x 1) + ar 2(- x 2) +…+ arj (- xj) +…+ arn (- xn) £ br < 0.
Иными словами r – е ограничение системы (3.4) не выполняется ни при каких значениях x 1; x 2; …, xn ³ 0
2. В r –ой строке существуют отрицательные элементы. Пусть, например, arj < 0. Рассмотрим j –й столбец и выберем в нем разрешающий элемент по принципу минимального симплексного отношения. Если нам повезет, то минимальное симплексное отношение будет соответствовать r –ой строке. Тогда после одного шага метода Штифеля, в соответствие с теоремой 3.1, мы добьемся того, что свободный член 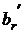 в r –ой строке станет неотрицательным. Остальные свободные члены не изменят своих знаков. Таким образом, количество отрицательных правых частей уменьшится. Поступая аналогично с остальными строками, мы, за конечное число шагов, добьемся того, что все свободные члены станут положительными. Тем самым мы найдем первоначальный опорный план.
в r –ой строке станет неотрицательным. Остальные свободные члены не изменят своих знаков. Таким образом, количество отрицательных правых частей уменьшится. Поступая аналогично с остальными строками, мы, за конечное число шагов, добьемся того, что все свободные члены станут положительными. Тем самым мы найдем первоначальный опорный план.
Если же разрешающий элемент не попадает в r –ю строку, то соответствующий шаг метода Штифеля не приведет к изменению знака свободного члена br. Мы совершаем своего рода «холостой шаг», после которого опять выбираем разрешающий элемент в j –ом столбце по принципу минимального симплексного отношения. И так мы поступаем до тех пор, пока разрешающий элемент не попадет в r –ю строку.
Рассмотрим следующие примеры.
Пример 3.1. Найти первоначальный опорный план задачи, заданной жордановой таблицей 3.2 (все переменные, участвующие в задаче, предполагаются неотрицательными).
|
| – x 1
| – x 2
| – x 3
| – x 4
|
| ti 3
|
| y 1
|
| –4
|
|
|
|
|
| y 2
|
|
| –2
|
| –3
| 1.5
|
| y 3
|
| –7
|
| –4
|
|
|
| y 4
| –2
|
| –4
|
|
| –
|
| z
| –1
| –15
|
|
|
| –
|
Табл. 3.2.
Решение. Для наглядности введем в таблицу 3.2 дополнительный правый столбец для симплексных отношений. Рассмотрим столбец свободных членов, расположенных под единицей. Среди чисел данного столбца есть одно отрицательное число b 2 = – 3. Следовательно, базисное решение (0; 0; 0; 0; 2; -3; 4; 6) не является опорным планом задачи (как всегда вначале идут иксовые, а затем игрековые координаты, в порядке возрастания индексов). Рассмотрим вторую строку таблицы и найдем в ней отрицательные числа. Такое число в данном случае единственно и равно a 23 = –2. Так как данное число расположено в третьем столбце, то будем разрешающий элемент искать именно в этом столбце. Для этого вычислим симплексные отношения для элементов третьего столбца и запишем их в правый дополнительный столбец таблицы 3.2.
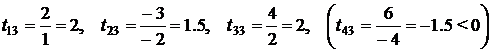 .
.
При этом симплексное отношение не вычисляется для последней строки, т.к. разрешающий элемент никогда не выбирается среди коэффициентов функции цели. Кроме того, на месте t 43 в таблице 3.2 стоит прочерк, т.к. симплексное отношение не может быть отрицательно. Сравнивая полученные симплексные отношения, мы приходим к выводу, что наименьшее симплексное отношение приходится на вторую строку. Следовательно, в качестве разрешающего элемента необходимо выбрать элемент a 23 = –2.
В данном случае нам повезло, т.к. разрешающий элемент попал в ту строку, в которой расположен отрицательный свободный член b 2 = –3. Следовательно, по теореме о минимальном симплексном отношении, после одного шага метода Штифеля, мы добьемся того, что знак свободного члена b 2¢ станет положительным, а остальные свободные члены при этом сохранят свои знаки. Мы приходим к таблице 3.3.
|
| – x 1
| – x 2
| – y 2
| – x 4
|
|
| y 1
|
| –2
| 0,5
|
| 0,5
|
| x 3
| –3
| –2
| –0,5
| –4
| 1,5
|
| y 3
|
| –3
|
|
|
|
| y 4
| –14
|
| –2
| –11
|
|
| z
|
| –1
| 3,5
|
| –10,5
|
Табл. 3.3.
Так как среди свободных членов в таблице 3.3 нет отрицательных чисел, то, следовательно, мы нашли первоначальный опорный план задачи:
X 0 = (0; 0; 1,5; 0; 0,5; 0; 1; 12).
Пример 3.2. Найти первоначальный опорный план задачи, заданной жордановой таблицей 3.4 (все переменные, участвующие в задаче, предполагаются неотрицательными).
|
| – x 1
| – x 2
| – x 3
| – x 4
|
| ti 3
|
| y 1
|
| –4
|
|
|
|
|
| y 2
|
|
| –2
|
| –3
| 1.5
|
| y 3
|
| –7
|
| –4
|
|
|
| y 4
| –2
|
| –4
|
|
| –
|
| z
| –1
| –15
|
|
|
| –
|
Табл. 3.4.
Решение. Данная задача отличается от предыдущей задачи всего одним числом (a 13 = 2). Мы по-прежнему имеем только один отрицательный свободный член b 2 = – 3. Рассмотрим вторую строку таблицы и найдем в ней отрицательные числа. Такое число, как и в предыдущем примере, единственно и равно a 23 = – 2. Так как данное число расположено в третьем столбце, то будем разрешающий элемент искать именно в этом столбце. Для этого вычислим симплексные отношения для элементов третьего столбца и запишем их в правый дополнительный столбец таблицы 3.2.
 .
.
Сравнивая полученные симплексные отношения, мы приходим к выводу, что наименьшее симплексное отношение приходится на первую строку. Следовательно, в качестве разрешающего элемента необходимо выбрать элемент a 13 = 2. В данном случае разрешающий элемент не попал в ту строку, в которой расположен отрицательный свободный член b 2 = –3. Мы вынуждены сделать «холостой шаг», после которого знак свободного члена


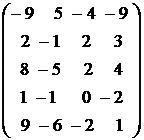 .
.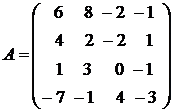 , составленной из координат этих векторов. Таким образом, данная задача решается аналогично задаче о нахождении ранга матрицы. Составим исходную жорданову таблицу 2.6 и сделаем два шага методом обыкновенных жордановых исключений, выбрав в качестве разрешающих элементов соответственно a 31 = 1 и b 23 = – 2. В результате приходим к таблице 2.8:
, составленной из координат этих векторов. Таким образом, данная задача решается аналогично задаче о нахождении ранга матрицы. Составим исходную жорданову таблицу 2.6 и сделаем два шага методом обыкновенных жордановых исключений, выбрав в качестве разрешающих элементов соответственно a 31 = 1 и b 23 = – 2. В результате приходим к таблице 2.8: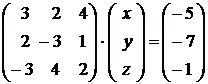 . (2.7)
. (2.7)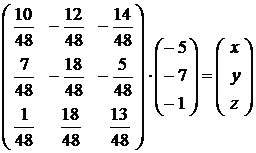 . (2.8)
. (2.8) и
и 
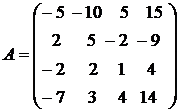 .
. .
.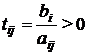 .
.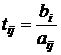 называются симплексными отношениями. Из определения следует, что все симплексные отношения строго больше нуля.
называются симплексными отношениями. Из определения следует, что все симплексные отношения строго больше нуля.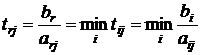 , (3.6)
, (3.6)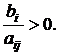 Тогда в качестве разрешающего элемента выберем элемент arj. Первое утверждение теоремы очевидно, так как после шага модифицированных жордановых исключений свободный член в разрешающей строке по формуле (1.10) будет равен
Тогда в качестве разрешающего элемента выберем элемент arj. Первое утверждение теоремы очевидно, так как после шага модифицированных жордановых исключений свободный член в разрешающей строке по формуле (1.10) будет равен 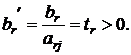
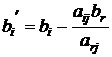 . (3.7)
. (3.7)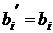 . То есть свободный член не изменился не только по знаку, но и по абсолютной величине. Если
. То есть свободный член не изменился не только по знаку, но и по абсолютной величине. Если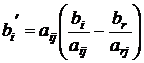 . (3.8)
. (3.8)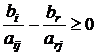 , так как
, так как 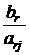 – минимальное симплексное отношение, а
– минимальное симплексное отношение, а 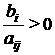 – произвольное симплексное отношение. Следовательно, в данной ситуации
– произвольное симплексное отношение. Следовательно, в данной ситуации 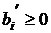 , как произведение двух неотрицательных чисел. То есть знак
, как произведение двух неотрицательных чисел. То есть знак 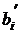 совпадает со знаком bi.
совпадает со знаком bi.  , как произведение противоположных по знаку чисел. То есть знак
, как произведение противоположных по знаку чисел. То есть знак 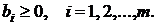 В данном случае первоначальное базисное решение (0,…, 0,…, 0, b 1,…, bi,…, bm), получающееся из таблицы 3.1, сразу является опорным планом задачи. Мы можем переходить ко второму этапу, т.е. к поиску оптимального плана.
В данном случае первоначальное базисное решение (0,…, 0,…, 0, b 1,…, bi,…, bm), получающееся из таблицы 3.1, сразу является опорным планом задачи. Мы можем переходить ко второму этапу, т.е. к поиску оптимального плана.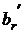 в r –ой строке станет неотрицательным. Остальные свободные члены не изменят своих знаков. Таким образом, количество отрицательных правых частей уменьшится. Поступая аналогично с остальными строками, мы, за конечное число шагов, добьемся того, что все свободные члены станут положительными. Тем самым мы найдем первоначальный опорный план.
в r –ой строке станет неотрицательным. Остальные свободные члены не изменят своих знаков. Таким образом, количество отрицательных правых частей уменьшится. Поступая аналогично с остальными строками, мы, за конечное число шагов, добьемся того, что все свободные члены станут положительными. Тем самым мы найдем первоначальный опорный план.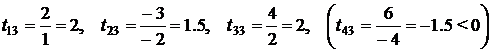 .
.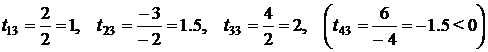 .
.