В общем случае суммадвух определителей (или их разность) не может быть записана в виде одногоопределителя:
 .
.
Эта сумма не может быть выражена через определители иначе, чем  ; например, она не может быть записана как
; например, она не может быть записана как  .
.

2.3. Разложение определителя по элементам строки (столбца)
Рассмотрим квадратную матрицу любого порядка  , где
, где 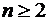
 ,
,
и её определитель.
Для вычисления такого определителя необходимо ввести понятие минора и алгебраического дополнения.



 Определение. Минором элемента
Определение. Минором элемента  определителя
определителя  порядка называется определитель
порядка называется определитель  порядка, полученный из исходного вычеркиванием
порядка, полученный из исходного вычеркиванием  строки и
строки и 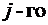 столбца (той строки и того столбца, на пересечении
столбца (той строки и того столбца, на пересечении  стоитэлемент
стоитэлемент  ).
).
Минор элемента  обозначается
обозначается 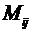 .
.
Здесь
 первый индекс означает номер строки,
первый индекс означает номер строки,
 второй – номер столбца, которые вычеркиваются.
второй – номер столбца, которые вычеркиваются.


 Например,
Например,
миноромэлемента  определителя
определителя





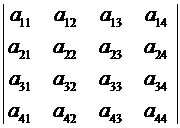 будетопределитель
будетопределитель  .
.



 В определителе 3-го порядка
В определителе 3-го порядка 
миноромэлемента 
являетсяопределитель 2-го порядка  .
.

 Миноромэлемента
Миноромэлемента  определителя
определителя 
является элемент  (определитель 1-го порядка).
(определитель 1-го порядка).




 Определение. Алгебраическим дополнением элемента
Определение. Алгебраическим дополнением элемента  называется его минор, взятый со знаком
называется его минор, взятый со знаком  .
.
Алгебраическое дополнениеэлемента  будем обозначать
будем обозначать  .
.
В соответствии с определением
 . (2.11)
. (2.11)
Для элементов, расположенных на главной диагонали, алгебраическое дополнение совпадает с минором:
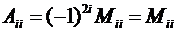 .
.
Очевидно,
если сумма  четная, то алгебраическое дополнение имеет тот же знак, что и минор;
четная, то алгебраическое дополнение имеет тот же знак, что и минор;
если сумма  нечетная, то знак изменится на противоположный знак.
нечетная, то знак изменится на противоположный знак.
Миноры двух соседних элементов строки (столбца) всегда приобретают противоположные знаки, т.к. при изменении  или
или  на одну единицу четность числа
на одну единицу четность числа  меняется.
меняется.
Распределение знаков у миноров (для получения алгебраических дополнений) можно изобразить следующим образом:
| +
| −
| +
| −
|
| −
| +
| −
| +
|
| +
| −
| +
| −
|
| −
| +
| −
| +
|
Теорема 2. 1 (разложения). Определитель 3-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
▲ Для определителя 2-го порядка это утверждение следует из формулы (2.4).
Докажем, что оно верно и дляопределителя третьего порядка.
Преобразуя правую часть формулы (2.8),
обозначив её левую часть  .
.
Т.к.



и
 ,
,
то
 , (2.12)
, (2.12)



 где
где  – определитель (2.8);
– определитель (2.8); 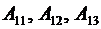 – алгебраические дополненияэлементов
– алгебраические дополненияэлементов  . ▼
. ▼
Формула (2.12) называется разложением определителя по элементам первой строки.
Аналогично получаются разложения соответственно по элементамдвух других строк и столбцов.


 Пример 1. Найти миноры и алгебраические дополнения элементов второй строки определителя
Пример 1. Найти миноры и алгебраические дополнения элементов второй строки определителя  .
.
▲ В данном случае  .
.
В соответствии с определениемминора получаем
 .
.
По формуле (2.11) находим алгебраические дополнения
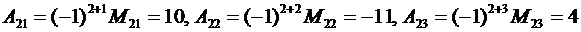 . ▼
. ▼


 Пример 2. Вычислить определитель
Пример 2. Вычислить определитель  , разложив его по элементам первой строки.
, разложив его по элементам первой строки.
▲ По формуле (2.12) получаем
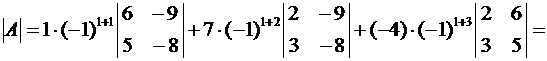
 ▼
▼


 Пример 3. Вычислить определитель
Пример 3. Вычислить определитель  , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца.
▲ По теореме 2.11 получаем  .
.
Далее, находим
 ;
;
 ;
;
откуда  . ▼
. ▼


 Пример 4. Вычислить определитель
Пример 4. Вычислить определитель 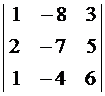 , преобразовавего и разложив по элементам 1-го столбца.
, преобразовавего и разложив по элементам 1-го столбца.
▲ Производя соответствующие преобразования, находим



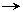
 .
.
Второй определитель получен в результате следующих преобразований 1-го определителя:
Ø первая строкаумножена на (-2) и сложенасо второй (св-во 8);
Ø первая строкаумножена на (-1) и сложенас третьей (св-во 8).
Далее второй определительразложен по элементам 1-го столбца по формуле, аналогичной формуле (2.12)
(второе и третье слагаемое этой суммы в этом примере не выписаны; они равны нулю, ибо содержатнулевые множители).
Для наглядности, перечисленные выше операции, будем указывать стрелками. ▼
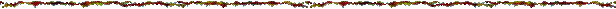
Теорема 2.2 (следствие из теоремы 1). Если все элементы  строки (столбца) определителя
строки (столбца) определителя  , кроме одного, например
, кроме одного, например  , равны нулю, то определитель равен произведению элемента
, равны нулю, то определитель равен произведению элемента  на его алгебраическое дополнение:
на его алгебраическое дополнение:
 . (2.13)
. (2.13)


 Пример 5. Вычислить определитель 4-го порядка
Пример 5. Вычислить определитель 4-го порядка



 ,
,
разложив его по элементам 2-го столбца.
▲ Т.к.  , то по формуле (2.13) получаем
, то по формуле (2.13) получаем



 ,
,
откуда, снова разлагая полученный определитель 3-го порядкапо элементам 2-го столбца, находим
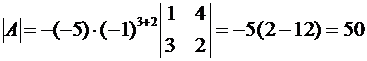 . ▼
. ▼
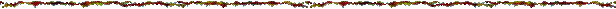
Теорема 2. 3 (замещения). Пусть  – определитель 3-го порядка. Сумма произведений алгебраических дополнений элементов какого-нибудь столбца (строки) на любые числа
– определитель 3-го порядка. Сумма произведений алгебраических дополнений элементов какого-нибудь столбца (строки) на любые числа 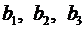 равна
равна
определителю  , который получается из данного определителя
, который получается из данного определителя  заменой указанного столбца (строки) столбцом (строкой) из чисел
заменой указанного столбца (строки) столбцом (строкой) из чисел 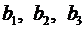 .
.
▲ Р ассмотрим определитель 3-го порядка  и определитель
и определитель  , полученныйиз данного определителя
, полученныйиз данного определителя  заменой 1-го столбца столбцомиз чисел
заменой 1-го столбца столбцомиз чисел 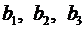 :
:


 , (2.14)
, (2.14)
На основании теоремы разложения 2.1

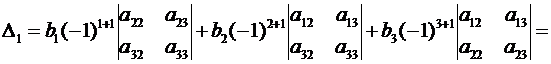

 . ▼
. ▼

Теорема 2. 4 (аннулирования). Сумма произведений элементов какой-нибудь строки (столбца) определителя 3-го порядка на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
▲ Пусть дан определитель  (
( (2.14)).
(2.14)).
Докажем, например, что
 ,
,
т.е. сумма произведений элементов 1-го столбцана алгебраические дополненияэлементов 2-го столбцаравнанулю.
По теореме 2.3 (в данном случае  ) имеем
) имеем

 .
.
Поскольку этот определитель равен нулю (как содержащийдва одинаковых столбца), то  . ▼
. ▼


2.4. Определение определителя  порядка
порядка
Чтобы подметить общее правило составленияопределителей матриц  порядка, присмотримся внимательнее к определителям 2-го и 3-го порядков.
порядка, присмотримся внимательнее к определителям 2-го и 3-го порядков.
Отвлекаясь пока от знака, поставим вопрос: чем характеризуются произведения, входящие в состав определителя?
1. Прежде всего, замечаем, что число сомножителей в каждом произведении равно порядку матрицы.
2. Далее, если обратимся к какому-нибудь конкретному произведению, то увидим, что в нём сомножители взяты по одному из каждой строки и по одному из каждого столбца.
3. Число различных произведений, из которых строится определитель матрицы  , равно числу всех перестановок
, равно числу всех перестановок 
( для определителя 2-го порядка),
для определителя 2-го порядка),
( для определителя 3-го порядка),
для определителя 3-го порядка),
т.е. равно 
( число произведений дляопределителя 2-го порядка) и
число произведений дляопределителя 2-го порядка) и
(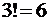 число произведений дляопределителя 3-го порядка).
число произведений дляопределителя 3-го порядка).
Так обстоит дело дляопределителей 2-го и 3-го порядков, и в этом мы убеждаемся, анализируя определения первого раздела.
Естественно предположить, что мы получим разумное определениеопределителя  порядка, если в его основу положим эту подмеченную закономерность.
порядка, если в его основу положим эту подмеченную закономерность.



 Определение 1 (предварительное). Определителем матрицы
Определение 1 (предварительное). Определителем матрицы 
 порядка называется
порядка называется
 сумма всех
сумма всех  произведений
произведений  элементов этой матрицы, взятых
элементов этой матрицы, взятых
 по одному из каждой строки и по одному из каждого столбца;
по одному из каждой строки и по одному из каждого столбца;
 при этом каждое произведение снабжено знаком плюс или минус по некоторому правилу.
при этом каждое произведение снабжено знаком плюс или минус по некоторому правилу.


 Предполагая, что
Предполагая, что  есть матрица 4-го порядка, рассмотрим несколько примеров.
есть матрица 4-го порядка, рассмотрим несколько примеров.
1. Произведения  и
и  не входят в определительматрицы
не входят в определительматрицы  , т.к. число сомножителей в них не равно порядку матрицы.
, т.к. число сомножителей в них не равно порядку матрицы.

2. Произведение  также не входит в определитель, т.к. два сомножителя,
также не входит в определитель, т.к. два сомножителя,  и
и 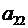 , принадлежат одному и тому же (второму) столбцу.
, принадлежат одному и тому же (второму) столбцу.

3. Произведения 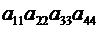 и
и  содержат множителипо одному из каждой строки и по одному из каждого столбца, – следовательно, они входят в составопределителя.
содержат множителипо одному из каждой строки и по одному из каждого столбца, – следовательно, они входят в составопределителя.

Замечание. Говоря об определителе матрицы, мы до сих пор предполагали, что порядок матрицы  .
.
Ясно, что вполне допустимо рассматривать таблицу, состоящую лишь из одного числа, т.е. квадратную матрицу 1-го порядка. Применив определениеопределителя к этому случаю, мы легко увидим, что если  , то
, то  , т.е. определитель матрицы 1-го порядка равен (единственному) элементу этой матрицы.
, т.е. определитель матрицы 1-го порядка равен (единственному) элементу этой матрицы.



 Определение 2. Определителем матрицы
Определение 2. Определителем матрицы  порядка
порядка  называется число, вычисляемое по следующему правилу:
называется число, вычисляемое по следующему правилу:
 . (2.15)
. (2.15)
Формула (2.15) выражает правило составления определителя  порядка по элементам первой строки соответствующей матрицы и по алгебраическим дополнениям этих элементов, являющимся определителями
порядка по элементам первой строки соответствующей матрицы и по алгебраическим дополнениям этих элементов, являющимся определителями  порядка, взятыми с надлежащими знаками.
порядка, взятыми с надлежащими знаками.
Из формулы (2.15)

 получаем формулу (2.4) (по определению),
получаем формулу (2.4) (по определению),

 – формулу (2.12) (по теореме разложения).
– формулу (2.12) (по теореме разложения).
Правило (2.15) дает возможность свести
Ø вычисленияопределителей матриц 4-го порядкак вычислениюопределителей матриц 3-го порядка,
Ø вычислениеопределителей матриц 5-го порядкак вычислениюопределителей матриц 4-го порядка и т.д.
Естественно, возникает вопрос,
 нельзя ли использовать для получения величиныопределителяэлементыи соответствующие им миноры не первой, а любой строки матрицы,
нельзя ли использовать для получения величиныопределителяэлементыи соответствующие им миноры не первой, а любой строки матрицы,
 а также вопрос о разложенииопределителяпо элементам любого столбца.
а также вопрос о разложенииопределителяпо элементам любого столбца.
Ответ на эти вопросы дают две основные теоремы, приводимые здесь без доказательств.
Теорема 2. 5. Каков бы ни был номер строки 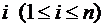 для определителя
для определителя  порядка справедлива формула
порядка справедлива формула
 ,
,
называемая разложением этого определителя по  строке.
строке.

Теорема 2. 6. Каков бы ни был номер столбца  для определителя
для определителя  порядка справедлива формула
порядка справедлива формула
 ,
,
называемая разложением этого определителя по  столбцу.
столбцу.

Отметим, что для определителей  порядка
порядка  также верны теоремы замещения и аннулирования.
также верны теоремы замещения и аннулирования.
Определители  порядка
порядка  обладают теми же свойствами, что и определители 2-го и 3-го порядков.
обладают теми же свойствами, что и определители 2-го и 3-го порядков.
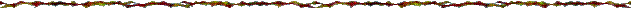






 .
. ; например, она не может быть записана как
; например, она не может быть записана как  .
.

 , где
, где 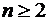
 ,
,


 Определение. Минором элемента
Определение. Минором элемента  определителя
определителя  порядка называется определитель
порядка называется определитель  порядка, полученный из исходного вычеркиванием
порядка, полученный из исходного вычеркиванием  строки и
строки и 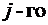 столбца (той строки и того столбца, на пересечении
столбца (той строки и того столбца, на пересечении  стоитэлемент
стоитэлемент 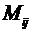 .
. первый индекс означает номер строки,
первый индекс означает номер строки,

 Например,
Например, определителя
определителя




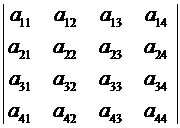 будетопределитель
будетопределитель  .
.


 В определителе 3-го порядка
В определителе 3-го порядка 

 .
.
 Миноромэлемента
Миноромэлемента  определителя
определителя 
 (определитель 1-го порядка).
(определитель 1-го порядка).


 Определение. Алгебраическим дополнением элемента
Определение. Алгебраическим дополнением элемента  .
. .
. . (2.11)
. (2.11)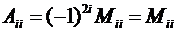 .
. четная, то алгебраическое дополнение имеет тот же знак, что и минор;
четная, то алгебраическое дополнение имеет тот же знак, что и минор; нечетная, то знак изменится на противоположный знак.
нечетная, то знак изменится на противоположный знак. или
или  на одну единицу четность числа
на одну единицу четность числа  .
.


 ,
, , (2.12)
, (2.12)


 где
где 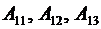 – алгебраические дополненияэлементов
– алгебраические дополненияэлементов  . ▼
. ▼
 Пример 1. Найти миноры и алгебраические дополнения элементов второй строки определителя
Пример 1. Найти миноры и алгебраические дополнения элементов второй строки определителя  .
.  .
. .
.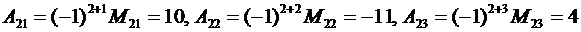 . ▼
. ▼
 , разложив его по элементам первой строки.
, разложив его по элементам первой строки.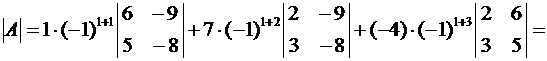
 ▼
▼
 , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца. .
. ;
; ;
; . ▼
. ▼
 Пример 4. Вычислить определитель
Пример 4. Вычислить определитель 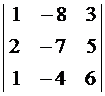 , преобразовавего и разложив по элементам 1-го столбца.
, преобразовавего и разложив по элементам 1-го столбца.


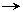
 .
.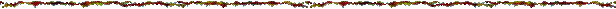
 строки (столбца) определителя
строки (столбца) определителя  , кроме одного, например
, кроме одного, например  . (2.13)
. (2.13)
 Пример 5. Вычислить определитель 4-го порядка
Пример 5. Вычислить определитель 4-го порядка


 ,
, , то по формуле (2.13) получаем
, то по формуле (2.13) получаем


 ,
,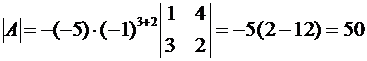 . ▼
. ▼ – определитель 3-го порядка. Сумма произведений алгебраических дополнений элементов какого-нибудь столбца (строки) на любые числа
– определитель 3-го порядка. Сумма произведений алгебраических дополнений элементов какого-нибудь столбца (строки) на любые числа 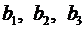 равна
равна , который получается из данного определителя
, который получается из данного определителя 

 , (2.14)
, (2.14)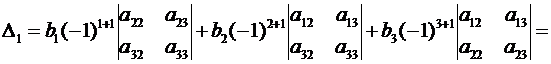

 . ▼
. ▼ (2.14)).
(2.14)). ,
, ) имеем
) имеем
 .
.

 порядка
порядка порядка, присмотримся внимательнее к определителям 2-го и 3-го порядков.
порядка, присмотримся внимательнее к определителям 2-го и 3-го порядков. , равно числу всех перестановок
, равно числу всех перестановок 
 для определителя 2-го порядка),
для определителя 2-го порядка), для определителя 3-го порядка),
для определителя 3-го порядка),
 число произведений дляопределителя 2-го порядка) и
число произведений дляопределителя 2-го порядка) и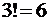 число произведений дляопределителя 3-го порядка).
число произведений дляопределителя 3-го порядка). порядка, если в его основу положим эту подмеченную закономерность.
порядка, если в его основу положим эту подмеченную закономерность.

 Определение 1 (предварительное). Определителем матрицы
Определение 1 (предварительное). Определителем матрицы 
 Предполагая, что
Предполагая, что  и
и  не входят в определительматрицы
не входят в определительматрицы  также не входит в определитель, т.к. два сомножителя,
также не входит в определитель, т.к. два сомножителя, 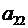 , принадлежат одному и тому же (второму) столбцу.
, принадлежат одному и тому же (второму) столбцу.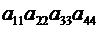 и
и  содержат множителипо одному из каждой строки и по одному из каждого столбца, – следовательно, они входят в составопределителя.
содержат множителипо одному из каждой строки и по одному из каждого столбца, – следовательно, они входят в составопределителя. .
. , то
, то  , т.е. определитель матрицы 1-го порядка равен (единственному) элементу этой матрицы.
, т.е. определитель матрицы 1-го порядка равен (единственному) элементу этой матрицы.


 . (2.15)
. (2.15) порядка по элементам первой строки соответствующей матрицы и по алгебраическим дополнениям этих элементов, являющимся определителями
порядка по элементам первой строки соответствующей матрицы и по алгебраическим дополнениям этих элементов, являющимся определителями  порядка, взятыми с надлежащими знаками.
порядка, взятыми с надлежащими знаками. получаем формулу (2.4) (по определению),
получаем формулу (2.4) (по определению), – формулу (2.12) (по теореме разложения).
– формулу (2.12) (по теореме разложения).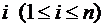 для определителя
для определителя  ,
, для определителя
для определителя  ,
, столбцу.
столбцу. также верны теоремы замещения и аннулирования.
также верны теоремы замещения и аннулирования.


