(n, k)-размещения с повторениями - это слова длины k в n -элементном алфавите. Используя правило произведения, нетрудно показать, что число различных (n, k)-размещений с повто-рениями  = nk. Действительно, каждая из k букв слова может быть выбрана n способами, независимо от других.
= nk. Действительно, каждая из k букв слова может быть выбрана n способами, независимо от других.
Примеры. 1. Число  слов длины k в алфавите {0, 1} равно 2 k; таково же число всех подмножеств k -элементного множества, поскольку множество однозначно задается своей характеристической функцией. Число k -значных двоичных чисел равно 2 k- 1, т.к. первая цифра должна равняться 1, а остальные могут быть любыми.
слов длины k в алфавите {0, 1} равно 2 k; таково же число всех подмножеств k -элементного множества, поскольку множество однозначно задается своей характеристической функцией. Число k -значных двоичных чисел равно 2 k- 1, т.к. первая цифра должна равняться 1, а остальные могут быть любыми.
2. Число k -значных десятичных чисел (т.е. имеющих ровно k знаков) равно 9•10 k- 1: их можно рассматривать как слова в алфавите {0, 1, 2,..., 9}, причем только первая цифра должна быть отлична от 0.
Число (n, k)-размещений без повторений  может быть также определено с помощью правила произведения. Первый из k элементов размещения может быть выбран n способами, второй - (n - 1) способами, поскольку элемент, выбранный первым, не должен быть повторен; аналогично, для третьего элемента (если k > 2) остается (n - 2) вариантов и т.д. Общая формула: k элементов могут быть выбраны
может быть также определено с помощью правила произведения. Первый из k элементов размещения может быть выбран n способами, второй - (n - 1) способами, поскольку элемент, выбранный первым, не должен быть повторен; аналогично, для третьего элемента (если k > 2) остается (n - 2) вариантов и т.д. Общая формула: k элементов могут быть выбраны
 = n • (n – 1) • (n – 2) •... • (n – k + 1)
= n • (n – 1) • (n – 2) •... • (n – k + 1)
способами: произведение k сомножителей, убывающих на единицу, начиная с n. Ту же формулу можно записать по-другому, используя обозначение n! = 1 • 2 •... • n:

 =
=  .
.
Для небольших значений k удобнее первое выражение.
Примеры.  = 7! / 4! = 7 • 6 • 5 = 210;
= 7! / 4! = 7 • 6 • 5 = 210;
 = 7! / 3! = 7 • 6 • 5 • 4 = 840;
= 7! / 3! = 7 • 6 • 5 • 4 = 840;
 = 7! / 2! = 7 • 6 • 5 • 4 • 3 = 2520.
= 7! / 2! = 7 • 6 • 5 • 4 • 3 = 2520.
Если k = 1, то  = n! / (n – 1)! = n;
= n! / (n – 1)! = n;
если k = n – 1, то  = n! / 1! = n!;
= n! / 1! = n!;
если k = n, то  = n! / 0! = [для единообразия формул удобно считать, что 0! = 1] = n!.
= n! / 0! = [для единообразия формул удобно считать, что 0! = 1] = n!.
Равенство чисел  и
и  естественно: если выбраны (n - 1) элементов из n, то единственный оставшийся элемент может быть выбран одним способом, а это и означает, что
естественно: если выбраны (n - 1) элементов из n, то единственный оставшийся элемент может быть выбран одним способом, а это и означает, что  =
=  . Поскольку
. Поскольку  =
=  , то число n-перестановок Pn равно n!.
, то число n-перестановок Pn равно n!.
Число (n, k)-сочетаний без повторенийобозначается символами  (применяется также обозначение
(применяется также обозначение  ) и называются также биномиальными коэффициентами, поскольку совпадают с коэффициентами формулы бинома Ньютона для n -й степени двучлена (x + y):
) и называются также биномиальными коэффициентами, поскольку совпадают с коэффициентами формулы бинома Ньютона для n -й степени двучлена (x + y):
(x + y) n =  • xk • yn-k. (7)
• xk • yn-k. (7)
Действительно, коэффициент при члене xk • yn-k равен числу способов, которыми из n одинаковых сомножителей (x + y) • (x + y) •... • (x + y) можно выбрать k (в них выбирается x, а в остальных y - произведение выбранных так множителей равно как раз xk• yn-k).
Для пересчета (n, k)-сочетаний без повторений удобно рассмотреть разбиение множества всех (n, k)-размещений без повторений на классы эквивалентности по отношению «иметь одинаковый состав элементов»; в один класс попадают размещения с одним и тем же составом элементов, но с различным их упорядочением; сочетания, отличающиеся составом элементов, попадают в различные классы. В каждом из классов содержатся упорядоченные конфигурации из одних и тех же k различных элементов, т.е. они представляют k -перестановки, и в каждом классе их число равно k!. Отсюда число ( n, k)-сочетаний без повторений  равно
равно  / k!, т.е.
/ k!, т.е.
 =
=  =
= 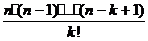 =
=  . (8)
. (8)
Для небольших значений k удобнее последнее выражение для  , поскольку здесь и в числителе, и в знаменателе – одинаковое число k сомножителей: в числителе - отрезок натурального ряда, начиная с n, в убывающем порядке; в знаменателе - отрезок натурального ряда [1, k ], начиная с 1, в возрастающем порядке. В частности,
, поскольку здесь и в числителе, и в знаменателе – одинаковое число k сомножителей: в числителе - отрезок натурального ряда, начиная с n, в убывающем порядке; в знаменателе - отрезок натурального ряда [1, k ], начиная с 1, в возрастающем порядке. В частности,  = 1,
= 1,  = n,
= n,  = n • (n-1) / 2. Удобно также считать, что
= n • (n-1) / 2. Удобно также считать, что  = 0, если k > n.
= 0, если k > n.
Примеры.
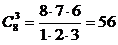 ;
;  ;
;  = 0.
= 0.
Приведем некоторые свойства биномиальных коэффициентов.
1)  .
.
Это следует как из формулы (2), так и из того, что выборка k элементов из n однозначно определяет дополнение: выборку (n – k) оставшихся элементов из n.
Поэтому, если k > n /2, то следует использовать данное равенство при вычислениях.
Отсюда и из предыдущих равенств следует
 ,
,  .
.
Примеры.  ;
;  =
=  .
.
В последнем равенстве в числителе и в знаменателе выделены скобками одинаковые сомножители.
2)  =
=  . Равенство следует из такого рассуждения. Зафиксируем некоторый элемент x n -элементного множества. Совокупность всех k -элементных подмножеств последнего (их число – левая часть равенства) разбивается на два непересекающихся класса: содержащих элемент x и не содержащих x. В первом классе
. Равенство следует из такого рассуждения. Зафиксируем некоторый элемент x n -элементного множества. Совокупность всех k -элементных подмножеств последнего (их число – левая часть равенства) разбивается на два непересекающихся класса: содержащих элемент x и не содержащих x. В первом классе  подмножеств: они содержат элемент x и
подмножеств: они содержат элемент x и
(k – 1) из остальных (n – 1) элементов. Во втором классе, очевидно,  элементов.
элементов.
Пример.  =
=  .
.
С последним тождеством связана схема, называемая треугольником Паскаля (рис. 1.1).

Рис. 1.1
Если перенумеровать по порядку строки этого треугольника числами 0, 1, 2,..., то i -я строка окажется состоящей из чисел  . В силу свойства 2 каждое число строки, кроме крайних, равных единице, можно получить как сумму двух ближайших чисел, находящихся над ним в предыдущем ряду. Это дает простой метод построения треугольника Паскаля и, тем самым, нахождения биномиальных коэффициентов: n -я строка задает коэффициенты бинома (x + y)n.
. В силу свойства 2 каждое число строки, кроме крайних, равных единице, можно получить как сумму двух ближайших чисел, находящихся над ним в предыдущем ряду. Это дает простой метод построения треугольника Паскаля и, тем самым, нахождения биномиальных коэффициентов: n -я строка задает коэффициенты бинома (x + y)n.
Замечание. Свойство 2 представляет собой пример рекуррентного (возвратного) соотноше-ния: величина  , рассматриваемая как функция двух аргументов n, k, выражается через значения этой же функции при других (здесь – меньших) значениях переменных.
, рассматриваемая как функция двух аргументов n, k, выражается через значения этой же функции при других (здесь – меньших) значениях переменных.
3) 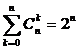 . Следует из подстановки x = y = 1 в формулу (7).
. Следует из подстановки x = y = 1 в формулу (7).
Примеры. Для n = 5: 1 + 5 + 10 + 10 + 5 + 1 = 32 = 25;
для n = 6: 1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26.
4)  = 0. Равенство следует из подстановки x = 1, y = -1 в формулу (7).
= 0. Равенство следует из подстановки x = 1, y = -1 в формулу (7).
Пример. Для n = 6: 1 - 6 + 15 - 20 + 15 - 6 + 1 = 0.
 5)
5)  = n • 2 n- 1. Чтобы убедиться в справедливости равенства, представим, что для каждого сочетания из n элементов { a 1, a 2,..., an } выписаны на отдельную карточку символы
= n • 2 n- 1. Чтобы убедиться в справедливости равенства, представим, что для каждого сочетания из n элементов { a 1, a 2,..., an } выписаны на отдельную карточку символы
ai 1, ai 2,..., aik, соответствующие элементам этого (k -элементного) сочетания: всего карточек -
2 n (по свойству 2). Тогда суммарное число символов на всех карточках можно подсчитать двояко:
а) суммарное число символов на карточках, содержащих ровно k символов, равно k •  ;
;
в левой части рассматриваемого равенства – общее число символов на всех карточках
для k = 0, 1,..., n;
б) если зачеркнуть некоторый символ аi на всех карточках, на которых он написан, то на них останутся всевозможные сочетания из остальных (n - 1) элементов (их число - 2 n- 1); значит символ аi написан ровно на 2 n- 1карточках. Общее число символов равно n • 2 n- 1- в правой части равенства.
Примеры. Для n = 5: 0 • 1 + 1 • 5 + 2 • 10 + 3 • 10 + 4 • 5 + 5 • 1 = 80 = 5 • 24.
Для n = 6: 0 • 1 + 1 • 6 + 2 • 15 + 3 • 20 + 4 • 15 + 5 • 6 + 6 • 1 = 192 = 6 • 25.
6)  =
=  (тождество Коши). Для доказательства удобно рассмотреть такую интерпретацию. Пусть из группы, состоящей из m мужчин и n женщин, выбирается делегация
(тождество Коши). Для доказательства удобно рассмотреть такую интерпретацию. Пусть из группы, состоящей из m мужчин и n женщин, выбирается делегация
k человек. Это можно сделать  способами. Все k -элементные подмножества нашего
способами. Все k -элементные подмножества нашего
(m + n)-элементного множества можно классифицировать по числу мужчин в делегации: любую
k -элементную делегацию, содержащую s мужчин, можно получить, выбирая сначала s мужчин одним из  способов, а затем (k - s) женщин одним из
способов, а затем (k - s) женщин одним из 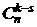 способов. По правилу произведения число таких делегаций равно
способов. По правилу произведения число таких делегаций равно  •
• 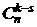 , а по правилу суммы общее число k -элементных делегаций такое, как в правой части равенства.
, а по правилу суммы общее число k -элементных делегаций такое, как в правой части равенства.
Пример.  =
=  =
=  •
•  +
+  •
•  +
+ 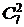 •
•  +
+  •
•  +
+  •
•  = [учитывая, что
= [учитывая, что
 = 0] = 7 • 1 + 21 • 3 + 35 • 3 + 35 • 1 = 210.
= 0] = 7 • 1 + 21 • 3 + 35 • 3 + 35 • 1 = 210.
[С другой стороны,  (см. пример п. 3)].
(см. пример п. 3)]. 
Чтобы получить число (n, k)-сочетаний с повторениями  , поставим в соответствие каждому такому сочетанию S (т.е. неупорядоченной k -выборке из n -элементного множества) слово в двухбуквенном алфавите {0, 1} следующим образом. Составим сначала набор T из
, поставим в соответствие каждому такому сочетанию S (т.е. неупорядоченной k -выборке из n -элементного множества) слово в двухбуквенном алфавите {0, 1} следующим образом. Составим сначала набор T из
n натуральных чисел { ai }, так что аi равно числу i -х элементов n -множества, входящих в данную k -выборку. Некоторые аi могут быть равны 0. Сумма n компонент этого кортежа равна k. Далее составим набор U из нулей и единиц, заменив каждое число аi на блок из аi единиц, перемежая эти блоки нулями:

Если некоторое аi = 0, то между соответствующими нулями не будет ни одной единицы.
Говоря по-другому, набор из (n - 1) нулей определяет n мест: слева от всего набора и справа
от каждого из нулей. На место i вставим ai единиц (некоторые ai, как сказано выше, могут равняться 0).
Например, (4, 7)-сочетанию S = (1, 1, 3, 4, 4, 4, 4) соответствует набор T = (2, 0, 1, 4), а ему, в свою очередь, набор из нулей и единиц U = 1100101111 (в сочетании S отсутствует элемент 2, поэтому после первого нуля сразу следует второй); (4, 7)-сочетанию S = (1, 2, 2, 2, 3, 3, 3) соответствует сначала набор T = (1, 3, 3, 0), а затем набор U = 1011101110 (в сочетании S отсутствует элемент 4, поэтому после последнего нуля пустое множество единиц).
В результате получаем набор U из (n - 1) нулей и k единиц, т.е. вектор длины (n - k + 1). Обратно, каждому такому вектору соответствует (n, k)-сочетание с повторениями: серии идущих подряд единиц определяют числа аi - их сумма равна k. Поэтому число (n, k)-сочетаний с повторениями  равно числу неупорядоченных наборов из (n - 1) нулей и k единиц,
равно числу неупорядоченных наборов из (n - 1) нулей и k единиц,
т.е. сочетаний с повторениями из (n + k - 1) по k:
 =
=  =
= 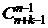 . (9)
. (9)
Равенство (9) можно получить и другим способом. Пусть (с 1, с 2,..., сk) - (n, k)-сочетание с повторениями, причем с 1≤ с 2≤ ... ≤ сk. Сопоставим ему выборку W = (d 1, d 2 ,..., dk), где d 1 = c 1+ 0,
d 2 = c 2+ 1, d 3 = c 3+ 2,... dk= ck+ k - 1. Все числа di различны, причем d 1 < d 2 <... < dk, поскольку в предыдущих суммах первые слагаемые не убывают, а вторые строго возрастают. Поэтому выборка (d 1, d 2 ,..., dk) может рассматриваться как (n+k- 1, k)-сочетание без повторений, записанное как упорядоченное по возрастанию. Обратно, каждому такому упорядоченному (n+k- 1, k)-сочетанию без повторений однозначно соответствует (n, k)-сочетание, возможно с повторениями, откуда следует равенство (9).
Пример.  =
=  =
=  = 6 • 5 / 2 = 15.
= 6 • 5 / 2 = 15.
В табл. 1.1 перечислены все 15 (3, 4)-сочетаний S с повторениями из 3 элементов по 4
(в 1-м столбце) вместе с соответствующими им наборами T (во 2-м столбце), U (в 3-м столбце) и соответствующими (6, 4)-сочетаниями без повторений W (в 4-м столбце).
Таблица 1.1
S T U W
1 1 1 1 4 0 0 1 1 1 1 0 0 1 2 3 4
1 1 1 2 3 1 0 1 1 1 0 1 0 1 2 3 5
1 1 1 3 3 0 1 1 1 1 0 0 1 1 2 3 6
1 1 2 2 2 2 0 1 1 0 1 1 0 1 2 4 5
1 1 2 3 2 1 1 1 1 0 1 0 1 1 2 4 6
1 1 3 3 2 0 2 1 1 0 0 1 1 1 2 5 6
1 2 2 2 1 3 0 1 0 1 1 1 0 1 3 4 5
1 2 2 3 1 2 1 1 0 1 1 0 1 1 3 4 6
1 2 3 3 1 1 2 1 0 1 0 1 1 1 3 5 6
1 3 3 3 1 0 3 1 0 0 1 1 1 1 4 5 6
2 2 2 2 0 4 0 0 1 1 1 1 0 2 3 4 5
2 2 2 3 0 3 1 0 1 1 1 0 1 2 3 4 6
2 2 3 3 0 2 2 0 1 1 0 1 1 2 3 5 6
2 3 3 3 0 1 3 0 1 0 1 1 1 2 4 5 6
3 3 3 3 0 0 4 0 0 1 1 1 1 3 4 5 6



 = nk. Действительно, каждая из k букв слова может быть выбрана n способами, независимо от других.
= nk. Действительно, каждая из k букв слова может быть выбрана n способами, независимо от других. слов длины k в алфавите {0, 1} равно 2 k; таково же число всех подмножеств k -элементного множества, поскольку множество однозначно задается своей характеристической функцией. Число k -значных двоичных чисел равно 2 k- 1, т.к. первая цифра должна равняться 1, а остальные могут быть любыми.
слов длины k в алфавите {0, 1} равно 2 k; таково же число всех подмножеств k -элементного множества, поскольку множество однозначно задается своей характеристической функцией. Число k -значных двоичных чисел равно 2 k- 1, т.к. первая цифра должна равняться 1, а остальные могут быть любыми. может быть также определено с помощью правила произведения. Первый из k элементов размещения может быть выбран n способами, второй - (n - 1) способами, поскольку элемент, выбранный первым, не должен быть повторен; аналогично, для третьего элемента (если k > 2) остается (n - 2) вариантов и т.д. Общая формула: k элементов могут быть выбраны
может быть также определено с помощью правила произведения. Первый из k элементов размещения может быть выбран n способами, второй - (n - 1) способами, поскольку элемент, выбранный первым, не должен быть повторен; аналогично, для третьего элемента (если k > 2) остается (n - 2) вариантов и т.д. Общая формула: k элементов могут быть выбраны
 .
. = 7! / 4! = 7 • 6 • 5 = 210;
= 7! / 4! = 7 • 6 • 5 = 210; = 7! / 3! = 7 • 6 • 5 • 4 = 840;
= 7! / 3! = 7 • 6 • 5 • 4 = 840; = 7! / 2! = 7 • 6 • 5 • 4 • 3 = 2520.
= 7! / 2! = 7 • 6 • 5 • 4 • 3 = 2520. = n! / (n – 1)! = n;
= n! / (n – 1)! = n; = n! / 1! = n!;
= n! / 1! = n!; = n! / 0! = [для единообразия формул удобно считать, что 0! = 1] = n!.
= n! / 0! = [для единообразия формул удобно считать, что 0! = 1] = n!. , то число n-перестановок Pn равно n!.
, то число n-перестановок Pn равно n!. (применяется также обозначение
(применяется также обозначение  ) и называются также биномиальными коэффициентами, поскольку совпадают с коэффициентами формулы бинома Ньютона для n -й степени двучлена (x + y):
) и называются также биномиальными коэффициентами, поскольку совпадают с коэффициентами формулы бинома Ньютона для n -й степени двучлена (x + y): • xk • yn-k. (7)
• xk • yn-k. (7) =
= 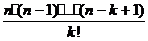 =
=  . (8)
. (8) = 1,
= 1,  = n,
= n,  = n • (n-1) / 2. Удобно также считать, что
= n • (n-1) / 2. Удобно также считать, что 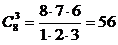 ;
;  ;
;  = 0.
= 0. .
. ,
,  .
. ;
;  =
=  .
. =
=  . Равенство следует из такого рассуждения. Зафиксируем некоторый элемент x n -элементного множества. Совокупность всех k -элементных подмножеств последнего (их число – левая часть равенства) разбивается на два непересекающихся класса: содержащих элемент x и не содержащих x. В первом классе
. Равенство следует из такого рассуждения. Зафиксируем некоторый элемент x n -элементного множества. Совокупность всех k -элементных подмножеств последнего (их число – левая часть равенства) разбивается на два непересекающихся класса: содержащих элемент x и не содержащих x. В первом классе  подмножеств: они содержат элемент x и
подмножеств: они содержат элемент x и  элементов.
элементов. =
=  .
.
 . В силу свойства 2 каждое число строки, кроме крайних, равных единице, можно получить как сумму двух ближайших чисел, находящихся над ним в предыдущем ряду. Это дает простой метод построения треугольника Паскаля и, тем самым, нахождения биномиальных коэффициентов: n -я строка задает коэффициенты бинома (x + y)n.
. В силу свойства 2 каждое число строки, кроме крайних, равных единице, можно получить как сумму двух ближайших чисел, находящихся над ним в предыдущем ряду. Это дает простой метод построения треугольника Паскаля и, тем самым, нахождения биномиальных коэффициентов: n -я строка задает коэффициенты бинома (x + y)n.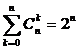 . Следует из подстановки x = y = 1 в формулу (7).
. Следует из подстановки x = y = 1 в формулу (7). = 0. Равенство следует из подстановки x = 1, y = -1 в формулу (7).
= 0. Равенство следует из подстановки x = 1, y = -1 в формулу (7). 5)
5)  = n • 2 n- 1. Чтобы убедиться в справедливости равенства, представим, что для каждого сочетания из n элементов { a 1, a 2,..., an } выписаны на отдельную карточку символы
= n • 2 n- 1. Чтобы убедиться в справедливости равенства, представим, что для каждого сочетания из n элементов { a 1, a 2,..., an } выписаны на отдельную карточку символы =
=  (тождество Коши). Для доказательства удобно рассмотреть такую интерпретацию. Пусть из группы, состоящей из m мужчин и n женщин, выбирается делегация
(тождество Коши). Для доказательства удобно рассмотреть такую интерпретацию. Пусть из группы, состоящей из m мужчин и n женщин, выбирается делегация  способов, а затем (k - s) женщин одним из
способов, а затем (k - s) женщин одним из 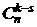 способов. По правилу произведения число таких делегаций равно
способов. По правилу произведения число таких делегаций равно  =
=  =
=  •
•  +
+  •
•  +
+ 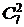 •
•  +
+  •
•  +
+  •
•  = [учитывая, что
= [учитывая, что  , поставим в соответствие каждому такому сочетанию S (т.е. неупорядоченной k -выборке из n -элементного множества) слово в двухбуквенном алфавите {0, 1} следующим образом. Составим сначала набор T из
, поставим в соответствие каждому такому сочетанию S (т.е. неупорядоченной k -выборке из n -элементного множества) слово в двухбуквенном алфавите {0, 1} следующим образом. Составим сначала набор T из 
 =
= 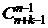 . (9)
. (9) =
=  =
=  = 6 • 5 / 2 = 15.
= 6 • 5 / 2 = 15.


