Механика
Механическое движение. Траектория движения. Пройденный путь. Скорость движения. Ускорение движения. Тангенциальное ускорение. Нормальное ускорение. Связь между ними.
Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. Траектория движения – это линия, которую описывает тело в результате своего движения. Пройденный путь – это отрезок траектории, пройденный точкой за некоторый промежуток времени. Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден

Ускорение движения - производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.

Тангенциальное ускорение - Составляющая ускорения, направленная вдоль скорости, Она характеризует изменение скорости по модулю.

Нормальное ускорение - составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости. Она характеризует изменение скорости по направлению.  Здесь R - радиус кривизны траектории в данной точке.
Здесь R - радиус кривизны траектории в данной точке.
Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
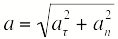
Работа силы. Консервативные и неконсервативные силы. Потенциальная энергия. Примеры формул потенциальной энергии взаимодействия тел. Кинетическая энергия поступательного и вращательного движения тел.
Работа силы - это мера действия силы, зависящая от её модуля и направления, а также от перемещения точки приложения силы.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения.
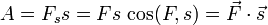
Здесь точкой обозначено скалярное произведение,  — вектор перемещения; подразумевается, что действующая сила
— вектор перемещения; подразумевается, что действующая сила 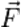 постоянна в течение всего того времени, за которое вычисляется работа.
постоянна в течение всего того времени, за которое вычисляется работа.
Консервативные силы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Диссипативные силы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту. Примерами диссипативных сил являются: силы вязкого или сухого трения и сила трения скольжения.
Потенциальная энергия тела – энергия, обусловленная взаимодействием тел. Потенциальная энергия 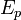 в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где  — масса тела,
— масса тела,  — ускорение свободного падения,
— ускорение свободного падения, 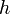 — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
Кинетическая энергия тела – это энергия тела, обусловленная его движением.
выделяют кинетическую энергию поступательного и вращательного движения.
Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.
Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.
Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.
Электричество и магнетизм.
Напряженность и потенциал электрического поля. Напряженность и потенциал электрического поля точечного заряда и системы точечных зарядов. Работа электрического поля. Разность потенциалов. Связь разности потенциалов с напряженностью электрического поля.
Направление силы Ампера определяется по правилу левой руки:если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера
Сила Лоренца
- сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы;
V - скорость заряда;
B - индукции магнитного поля;
a - угол между вектором скорости заряда и вектором магнитной индукции.
Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы
Движение частицы с зарядом q и массой m в однородном постоянном электрическом поле напряженностью  . Напряженность поля в этом случае не зависит ни от координат, ни от времени (такое поле возникает, например, в заряженном плоском конденсаторе, отсоединенном от источника). Следовательно, на заряженную частицу со стороны поля действует постоянная сила, которая сообщает частице постоянное ускорение
. Напряженность поля в этом случае не зависит ни от координат, ни от времени (такое поле возникает, например, в заряженном плоском конденсаторе, отсоединенном от источника). Следовательно, на заряженную частицу со стороны поля действует постоянная сила, которая сообщает частице постоянное ускорение  .
.
При движении заряженной частицы в однородном постоянном магнитном поле на нее действует сила Лоренца  . Если начальная скорость
. Если начальная скорость  частицы перпендикулярна вектору магнитной индукции
частицы перпендикулярна вектору магнитной индукции  поля, то заряженная частица движется по окружности
поля, то заряженная частица движется по окружности
2.5 Работа магнитного поля при движении проводника с током. Магнитный поток. Индуктивность контура. Индуктивность соленоида
Работа, совершаемая магнитным полем, равна

так как l d x= d S — площадь, пересекаемая проводником при его перемещении в магнитном поле, B d S= dФ — поток вектора магнитной индукции, пронизывающий эту площадь.
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Φ = B · S · cos α
Единица измерения магнитного потока в систем СИ - 1 Вебер (1 Вб).
1 Вб = 1 Тл · 1 м2
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.
В формуле

 — магнитный поток,
— магнитный поток,  — ток в контуре,
— ток в контуре,  — индуктивность.
— индуктивность.
формула для индуктивности соленоида (без сердечника):

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель 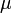 — относительную магнитную проницаемость[14] сердечника:
— относительную магнитную проницаемость[14] сердечника:

Колебания и волны.
Механические колебания. Смещение, период, частота, амплитуда фаза и циклическая частота колебаний. Гармонические колебания. Уравнение гармонических колебаний. Скорость и ускорение движения при гармонических колебаниях. Связь ускорения со смещением.
Механические колебания – это движение тела, в ходе которого оно многократно движется по одной и той же траектории и проходит при этом одни и те же точки пространства. Физическая величина, которая изменяется со временем при колебательном движении, называется смещением.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний T — это время одного полного колебания. Можно сказать, что за период
тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду: 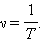 Частота измеряется в
Частота измеряется в
герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Фаза является свойством колебательного движения, которое характеризует величину смещения тела в любой момент времени. Измеряется фаза в радианах.
Циклическая частота ω = 2πν. Она связана с периодом отношением 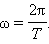
Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. x=x0cos(ω0t + φ0)
Скорость vx=-A ω sin(ω0t + φ0)
Ускорение ax=A ω2 cos(ω0t + φ0)
Связь ускорения со смещением: ax=- ω2x
Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы
Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание)
Частота — число колебаний в единицу времени
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота  (рад/сек, Гц, сек−1), показывающая число колебаний за
(рад/сек, Гц, сек−1), показывающая число колебаний за 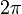 единиц времени:
единиц времени:
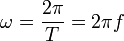
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

или
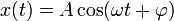 ,
,
где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, 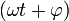 — полная фаза колебаний,
— полная фаза колебаний, 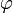 — начальная фаза колебаний.
— начальная фаза колебаний.
Согласно определению скорости, скорость – это производная от координаты по времени 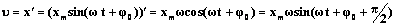
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.
Величина  - максимальная скорость колебательного движения (амплитуда колебаний скорости).
- максимальная скорость колебательного движения (амплитуда колебаний скорости).
Согласно определению ускорения, ускорение – это производная от скорости по времени:
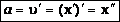 -
-
вторая производная от координаты по времени. Тогда: 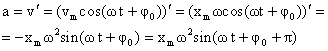 .
.
Гармонические колебания изображаются графически методом вращающегося вектора
амплитуды, или методом векторных диаграмм.
Для этого из произвольной точки О, выбранной на оси x под углом j,
равным начальной фазе колебания, откладывается вектор А, модуль которого равен
амплитуде А рассматриваемого колебания
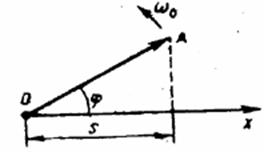
Если этот вектор привести во вращение с угловой скоростью w0, равной циклическойчастоте колебаний, то проекция конца вектора будет перемещаться по оси
x и принимать значения от -
А до +
А, а колеблющаяся величина будетизменяться со временем по закону s =
A cos (w0 t +j). Таким образом,гармоническое колебание можно представить проекцией на некоторую
произвольно выбранную ось вектора амплитуды А, отложенного из произвольнойточки оси под углом j, равным начальной фазе, и вращающегося с угловойскоростью w0 вокруг этой точки.
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения на p (говорят, что колебания происходят в противофазе).
Величина 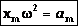
- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем:  ,
,
а для случая нулевой начальной фазы: 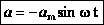
Сравним выражения для смещения и ускорения при гармонических колебаниях:
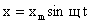 и
и  .
.
Можно записать: 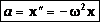 -
-
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
Представление гармонических колебаний в виде вращающегося вектора. Сложение двух гармонических колебаний с одинаковыми частотами, совершающихся в одном направлении. Условия усиления и максимального усиления колебаний.
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 - φ1):
1) φ2 - φ1 = ±2mπ (m = 0, 1, 2,...), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 - φ1 = ±(2m+1)π (m = 0, 1, 2,...), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Амплитуда результирующего колебания максимальна и равна сумме амплитуд слагаемых колебаний: если разность фаз этих колебаний составляет четное число п; если же разность фаз составляет нечетное число п, то амплитуда результирующего колебания минимальна и равна разности амплитуд слагаемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω<<ω. Выберем начало отсчета так, чтобы начальные фазы обоих колебаний были равны нулю:
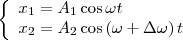
Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим
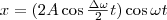 (3)
(3)
Результирующее колебание (3) можно считать как гармоническое с частотой ω, амплитуда Аσ которого изменяется по следующему периодическому закону:
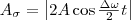 (4)
(4)
Частота изменения Аσ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:

Период биений

Вид зависимости (3) показан на рис. 2, где сплошные жирные линии представляют график результирующего колебания (3), а огибающие их линии - график медленно меняющейся согласно уравнению (4) амплитуды.
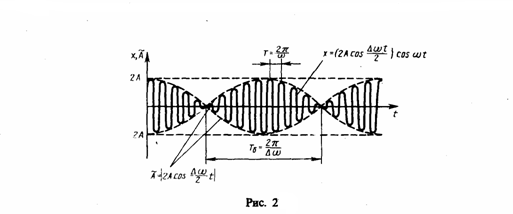
Рис.2
Нахождение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями — наиболее часто используемый на практике метод сравнения измеряемой величины с эталонной. Метод биений применяется для настройки музыкальных инструментов, анализа слуха и т. д.
При исследовании сложного колебательного процесса нужно знать, что любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции (наложения) одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, которые кратны циклической частоте ω0:
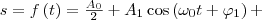
 (5)
(5)
Представление в виде (5) любой периодической функции связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье. Слагаемые ряда Фурье, которые определяют гармонические колебания с частотами ω0, 2ω0, 3ω0,..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания.
Упругие волны. Механизмы и условия возникновения упругих волн. Поперечные и продольные упругие волны, условия их возникновения. Формулы скорости упругих волн в различных средах. Длина волны. Циклическое волновое число. Уравнение плоской волны.
Упругие волны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.
В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.
В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.
В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.
Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.
Наиболее распространёнными типами упругих волн в твёрдых телах являются:
-продольные волны;
-поперечные волны, движение частиц перпендикулярно направлению распространения волны;
-поверхностные волны (например волны Рэлея, где движение частиц происходит по эллипсам);
-волны в тонких пластинах — волны Лэмба.
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах. Величина 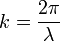 , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
Электромагнитная волна. Условия и механизмы ее возникновения. Скорость и длина электромагнитной волны в вакууме и различных средах. Показатель преломления волны. Шкала электромагнитных волн. Характеристики электромагнитных волн различных интервалов длин волн.
Электромагнитные волны— распространяющееся в пространстве возмущение (изменение состояния)электромагнитного поля (то есть, взаимодействующих друг с другом электрического и магнитного полей).
Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.
Источником эм волн являются ускоренно движущиеся электрические заряды, а также переменные, электрические и магнитные поля.
Эм волны распространяются в вакууме со скоростью света, скорость и длина зависят от среды. n=c/v=sqrt(эпсилон*мю).-абсолютный показатель преломления.
Электромагнитные волны классифицируются по длине волны или связанной с ней частотой волны:
1) Низкочастотные волны;
2) Радиоволны;
3) Инфракрасное излучение;
4) Световое излучение;
5) Рентгеновское излучение;
6) Гамма излучение.
Низкочастотные волны представляют собой электромагнитные волны, частота колебаний которых не превышает 100 КГц.
Радиоволны представляют собой электромагнитные волны, длины которых превосходят 1 мм (частота меньше 3 1011гц = 300 Ггц) и менее 3 км (выше 100 кГц).
Радиоволны делятся на:
1. Длинные волны в интервале длин от 3 км до 300 м(частота в диапазоне 105 гц -106гц= 1 МГц);
2. Средние волны в интервале длин от 300 м до 100 м (частота в диапазоне 106 гц -3*106гц=3мгц);
3. Короткие волны в интервале длин волн от 100м до 10м (частота в диапазоне 3106гц-3107гц=30мгц);
4. Ультракороткие волны с длиной волны меньше 10м(частота больше 3107гц=30Мгц).
Ультракороткие волны в свою очередь делятся на:
а) метровые волны;
б) сантиметровые волны;
в) миллиметровые волны;
Инфракрасное,световое, включаяультрафиолетовое, излучения составляют оптическую область спектра электромагнитных волн. Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 210-6м= 2мкм до 10-8м=10нм (по частоте от1.51014гц до 31016гц). Верхняя граница оптического диапазона определяется длинноволновой границей инфракрасного диапазона, а нижняя коротковолновой границей ультрафиолета.
В области рентгеновского и гамма излучения на первый план выступают квантовые свойства излучения.
Рентгеновское излучение составляют электромагнитные волны с длиной от50 нм до 10-3нм.
Гамма излучение составляют электромагнитные волны с длиной волны меньше 10-2нм.
Основные понятия и характеристики теплового излучения
Отражающая способность тела
Отражающая способность тела —  — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот
— функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот  вблизи
вблизи 

где  — поток энергии, отражающейся от тела.
— поток энергии, отражающейся от тела.
 — поток энергии, падающий на тело в области
— поток энергии, падающий на тело в области  вблизи
вблизи 
Абсолютно черное тело — это физическая абстракция (модель), под которой понимают тело, полностью поглощающее всё падающее на него электромагнитное излучение
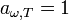 — для абсолютно черного тела
— для абсолютно черного тела
Серое тело — это такое тело, коэффициент поглощения которого не зависит от частоты, а зависит только от температуры
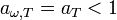 — для серого тела
— для серого тела
Объемная плотность энергии излучения —  — функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот
— функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот
Спектральная плотность энергии —  — функция частоты и температуры, связанная с объемной плотностью излучения формулой:
— функция частоты и температуры, связанная с объемной плотностью излучения формулой:

Следует отметить, что спектральная плотность энергетической светимости для абсолютно черного тела связана со спектральной плотностью энергии следующим соотношением:
 — для абсолютно черного тела
— для абсолютно черного тела
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
Мощность излучения абсолютно чёрного тела прямо пропорциональна площади поверхности и четвёртой степени температуры тела:

|
где  - степень черноты (для всех веществ
- степень черноты (для всех веществ 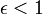 , для абсолютно черного тела
, для абсолютно черного тела  ). При помощи закона Планка для излучения, постоянную
). При помощи закона Планка для излучения, постоянную 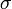 можно определить как
можно определить как
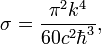
где  — постоянная Планка,
— постоянная Планка,  — постоянная Больцмана,
— постоянная Больцмана,  — скорость света.
— скорость света.
Численное значение  Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4.
Закон излучения Кирхгофа- Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Закон смещения Вина даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.
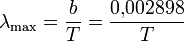
где T — температура в кельвинах, а  — длина волны с максимальной интенсивностью в метрах. Следует отметить, что коэффициент b, называемый постоянной Вина, и имеющий значение
— длина волны с максимальной интенсивностью в метрах. Следует отметить, что коэффициент b, называемый постоянной Вина, и имеющий значение 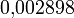 , в данной формуле имеет при этом размерность [ мК ]
, в данной формуле имеет при этом размерность [ мК ]
Согласно постулату Планка: энтропия правильно сформированного кристалла индивидуального вещества при абсолютной температуре Т=О К равна нулю. Правильно сформированный (идеальный) кристалл—это бездефектный кристалл, в решетке которого атомы занимают узлы в строгом соответствии с геометрическими законами.
4.3 Фотон — элементарная частица, переносчик электромагнитного взаимодействия, квант электромагнитного поля. Фотоны обозначаются буквой γ, поэтому их часто называют гамма-квантами (особенно фотоны высоких энергий); эти термины практически синонимичны.
Корпускуля́рно-волново́й дуали́зм (или Ква́нтово-волново́й дуали́зм) — принцип, согласно которому любой объект может проявлять какволновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепцияквантованных полей в квантовой теории поля.
Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойстваэлектромагнитных волн. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны.
Такие явления, как интерференция и дифракция света, убедительно свидетельствуют о волновой природе света. В то же время закономерности равновесного теплового излучения, фотоэффекта и эффекта Комптона можно успешно истолковать с классической точки зрения только на основе представлений о свете, как о потоке дискретных фотонов. Однако волновой и корпускулярный способы описания света не противоречат, а взаимно дополняют друг друга, так как свет одновременно обладает и волновыми и корпускулярными свойствами.
Волновые свойства света играют определяющую роль в закономерностях его интерференции, дифракции, поляризации, а корпускулярные — в процессах взаимодействия света с веществом. Чем больше длина волны света, тем меньше импульс и энергия фотона и тем труднее обнаружить корпускулярные свойства света. Например, внешний фотоэффект происходит только при энергиях фотонов, больших или равных работе выхода электрона из вещества. Чем меньше длина волны электромагнитного излучения, тем больше энергия и импульс фотонов и тем труднее обнаружить волновые свойства этого излучения. Например, рентгеновское излучение дифрагирует только на очень «тонкой» дифракционной решетке — кристаллической решетке твердого тела.
4.4)ЯДЕРНАЯМОДЕЛЬАТОМА. Результатыквантово-механическогорассмотренияповедения
электронавводородоподобноматоме. Излучениеипоглощениеэнергииатомамиимолекулами.
_____________________________
Ядерная (планетарная) модельатома.
Планетарнаямодельатома, илимодельРезерфорда, - историческаямодельстроенияатома, которуюпредложилЭрнестРезерфордврезультатеэкспериментасрассеиваниемальфа-частиц. Поэтоймоделиатомсостоитизнебольшогоположительнозаряженногоядра, вкоторомсосредоточенапочтивсямассаатома, вокругкоторогодвижутсяэлектроны, - подобнотому, какпланетыдвижутсявокругСолнца. Планетарнаямодельатомасоответствуетсовременнымпредставлениямостроенииатомасучётомтого, чтодвижениеэлектроновимеетквантовыйхарактеринеописываетсязаконамиклассическоймеханики. ИсторическипланетарнаямодельРезерфордапришланасмену «моделисливовогопудинга» ДжозефаДжонаТомсона, котораяпостулирует, чтоотрицательнозаряженныеэлектроныпомещенывнутрьположительнозаряженногоатома.
Атом и молекула могут находиться в стационарных энергетических состояниях. В этих состояниях они не излучают и не поглощают энергии. Энергетические состояния схематически изображают в виде уровней (см., например, рис. 28.13). Самый нижний уровень энергии - основной - соответствует основному состоянию.
При квантовых переходах атомы и молекулы скачкообразно переходят из одного стационарного состояния в другое, с одного энергетического уровня на другой.
Изменение состояния атомов связано с энергетическими переходами электронов. В молекулах энергия может изменяться не только в результате электронных переходов, но и вследствие изменения колебания атомов и переходов между вращательными уровнями.
При переходе с более высоких энергетических уровней на нижние атом или молекула отдает энергию, при обратных переходах - поглощает. Атом в основном состоянии способен только поглощать энергию.
Различают два типа квантовых переходов:
1) без излучения или поглощения электромагнитной энергии атомом или молекулой. Такой безызлучательный переход происходит при взаимодействии атома или молекулы с другими частица-
ми, например в процессе столкновения. Различают неупругое столкновение, при котором изменяется внутреннее состояние атома и осуществляется безызлучательный переход, и упругое - с изменением кинетической энергии атома или молекулы, но с сохранением внутреннего состояния; 2) с излучением или поглощением фотона.
Энергия фотона равна разности энергий начального и конечного стационарных состояний атома или молекулы:

Формула выражает закон сохранения энергии.
В зависимости от причины, вызывающей квантовый переход с испусканием фотона, различают два вида излучения. Если эта причина внутренняя и возбужденная частица самопроизвольно переходит на нижний энергетический уровень, такое излучение называют спонтанным. Оно случайно и хаотично по времени, частоте (могут быть переходы между разными подуровнями), по направлению распространения и поляризации. Обычные источники света испускают в основном спонтанное излучение. Другое излучение вынужденное, или индуцированное. Оно возникает при взаимодействии фотона с возбужденной частицей, если энергия фотона равна разности уровней энергий. В результате вынужденного квантового перехода от частицы будут распространяться в одном направлении два одинаковых фотона: один - первичный, вынуждающий, а другой - вторичный, испущенный.
Излучаемая атомами или молекулами энергия формирует спектр испускания, а поглощаемая - спектр поглощения.
4.5 Атомноеядросостоитизнуклонов — положительнозаряженныхпротоновинейтральныхнейтронов, которыесвязанымеждусобойприпомощи сильноговзаимодействия. Протонинейтронобладаютсобственныммоментомколичествадвижения (спином), равным [сн 1] исвязаннымсниммагнитныммоментом.
Атомноеядро, рассматриваемоекакклассчастицсопределённымчисломпротоновинейтронов, принятоназыватьнуклидом.
Радиоактивность — этосамопроизвольноеизменениесоставаатомногоядра, котороепроисходитнеменеечемчерез 10-12 спослеегорождения. Количественноеограничениеобусловленокакразэкспериментамисбомбардировкойатомныхядер. Еслистабильноеядроразваливаетсясразупослепопаданиявнегоснарядаатомнойартиллерии, неуспевпросуществоватьвизмененномвидедажетакойничтожнократкийпромежутоквремени, значит, явлениетакогораспаданеотноситсякрадиоактивности.
Первопричинойрадиоактивностиявляетсяпротивоборствовнутриядрадвухсил — электрическогоотталкиванияиядерногостягивания. Протоныядра, каквсякиеодноименнозаряженныечастицы, взаимноотталкиваются, стремятсяразлететься. Ядерныесилысближаютнуклоны, препятствуютразлетупротонов. Судьбаядразависит, такимобразом, отсоотношенияэтихсил, аболееконкретно — отсоотношениячислапротоновинейтроноввядре; Протоны — носителикак
«склеивающих» ядерныхсил, такирасталкивающихэлектрических. Лишенныезаряданейтронывносятвкладлишьвстягиваниеядра.
Числопротоноввядреопределяетатомныйномерэлемента, числоэлектроновватомеи, сталобыть, егохимическиесвойства. Содержаниенейтроноввтакомядреможетколебаться, носвойствавещества, заисключениематомноймассы, приэтомсущественнонеразличаются. Поэтомуядрасодинаковымчисломпротонов, норазнымколичествомнейтроновпредставляютсобойвариантыатомоводногоэлемента, располагаютсяводнойклеткетаблицыМенделееваиносятназваниеизотопы, тоестьрасположенныеводномместе. Большинствоэлементовипредставляетсобойсмесьнесколькихстабильныхизотопов.
Делениеисинтезядер (nuclear fission and fusion). Делениепредставляетсобойраспад (расщепление) атомногоядранадвеприбл. равныечасти (осколки), сопровождающийсявыделениемэнергиии, вотд. случаях, испусканиемоднойилинеск. частиц, напр, нейтронов. Нек-рыетяжелыеядрамогутделитьсясамопроизвольно (спонтанно), болеелегкие - вслучаесоударениясдр. ядрами, обладающимибольшойэнергией. Крометого, тяжелыеядра, напр, атомовурана, способныделитьсяподвоздействиембомбардировкинейтронами, апосколькуприэтомиспускаютсяновыенейтроны, процессможетстатьсамоподдерживающимся, т.е. возникаетцепнаяреакция. Входетакойреакцииделенияпроисходитвысвобождениебольшогокол-ваэнергии. Вядерныхреакторахпротекаютуправляемыецепныере<








 Здесь R - радиус кривизны траектории в данной точке.
Здесь R - радиус кривизны траектории в данной точке.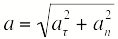
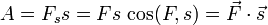
 — вектор перемещения; подразумевается, что действующая сила
— вектор перемещения; подразумевается, что действующая сила 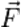 постоянна в течение всего того времени, за которое вычисляется работа.
постоянна в течение всего того времени, за которое вычисляется работа.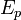 в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
 — масса тела,
— масса тела,  — ускорение свободного падения,
— ускорение свободного падения, 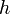 — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.

 . Напряженность поля в этом случае не зависит ни от координат, ни от времени (такое поле возникает, например, в заряженном плоском конденсаторе, отсоединенном от источника). Следовательно, на заряженную частицу со стороны поля действует постоянная сила, которая сообщает частице постоянное ускорение
. Напряженность поля в этом случае не зависит ни от координат, ни от времени (такое поле возникает, например, в заряженном плоском конденсаторе, отсоединенном от источника). Следовательно, на заряженную частицу со стороны поля действует постоянная сила, которая сообщает частице постоянное ускорение  .
. . Если начальная скорость
. Если начальная скорость  частицы перпендикулярна вектору магнитной индукции
частицы перпендикулярна вектору магнитной индукции  поля, то заряженная частица движется по окружности
поля, то заряженная частица движется по окружности

 — магнитный поток,
— магнитный поток,  — ток в контуре,
— ток в контуре,  — индуктивность.
— индуктивность.
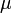 — относительную магнитную проницаемость[14] сердечника:
— относительную магнитную проницаемость[14] сердечника:
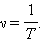 Частота измеряется в
Частота измеряется в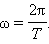
 (рад/сек, Гц, сек−1), показывающая число колебаний за
(рад/сек, Гц, сек−1), показывающая число колебаний за 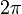 единиц времени:
единиц времени: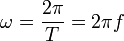

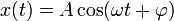 ,
,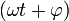 — полная фаза колебаний,
— полная фаза колебаний, 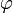 — начальная фаза колебаний.
— начальная фаза колебаний.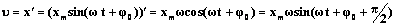
 - максимальная скорость колебательного движения (амплитуда колебаний скорости).
- максимальная скорость колебательного движения (амплитуда колебаний скорости).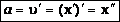 -
-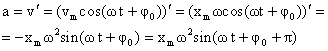 .
.
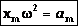
 ,
,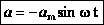
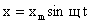 и
и  .
.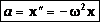 -
-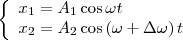
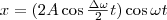 (3)
(3)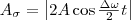 (4)
(4)


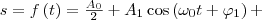
 (5)
(5)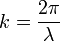 , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты. — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот
— функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот  вблизи
вблизи 
 — поток энергии, отражающейся от тела.
— поток энергии, отражающейся от тела. — поток энергии, падающий на тело в области
— поток энергии, падающий на тело в области 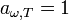 — для абсолютно черного тела
— для абсолютно черного тела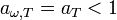 — для серого тела
— для серого тела — функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот
— функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот — функция частоты и температуры, связанная с объемной плотностью излучения формулой:
— функция частоты и температуры, связанная с объемной плотностью излучения формулой:
 — для абсолютно черного тела
— для абсолютно черного тела
 - степень черноты (для всех веществ
- степень черноты (для всех веществ 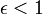 , для абсолютно черного тела
, для абсолютно черного тела  ). При помощи закона Планка для излучения, постоянную
). При помощи закона Планка для излучения, постоянную 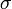 можно определить как
можно определить как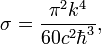
 — постоянная Планка,
— постоянная Планка,  — постоянная Больцмана,
— постоянная Больцмана,  — скорость света.
— скорость света. Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4.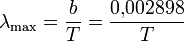
 — длина волны с максимальной интенсивностью в метрах. Следует отметить, что коэффициент b, называемый постоянной Вина, и имеющий значение
— длина волны с максимальной интенсивностью в метрах. Следует отметить, что коэффициент b, называемый постоянной Вина, и имеющий значение 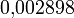 , в данной формуле имеет при этом размерность [ мК ]
, в данной формуле имеет при этом размерность [ мК ]


